大模型--ReLU激活函数--31
1 参考
“死亡”ReLUs
邱锡鹏老师的《神经网络与深度学习》
2. 基础
Sigmoid型函数的两端饱和,
ReLU函数为左饱和函数,且在x > 0时导数为1,在一定程度上缓解了神经网络的梯度消失问题,加速梯度下降的收敛速度。
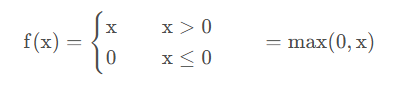
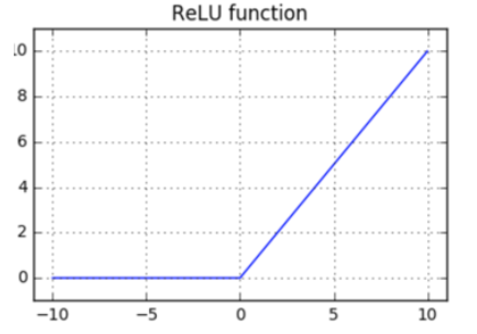
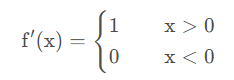
ReLU也是非线性函数,它将低于或等于 0 的神经元输入都计算成 0。
z = np.maximum(0, np.dot(W, x)) # forward pass
dz_dW = np.outer(z > 0, x) # backward pass: local gradient for W
反向传播比较难理解:
- z > 0:这部分创建了一个布尔掩码,
其大小与 z 相同。对于 z 中每一个元素,如果该元素大于零,则相应位置的布尔值为 True(或等效地转换为1),否则为 False(或0)。 - np.outer(..., x),这里我们用的是布尔掩码(经过隐式转换成1s和0s)和输入向量 x 的外积。结果是一个形状为 (len(z), len(x)) 的矩阵,也就是权重矩阵 W 的梯度。
当 z[i] > 0 时,dz_dW[i, :] 等于 x;
当 z[i] <= 0 时,dz_dW[i, :] 全部为零。
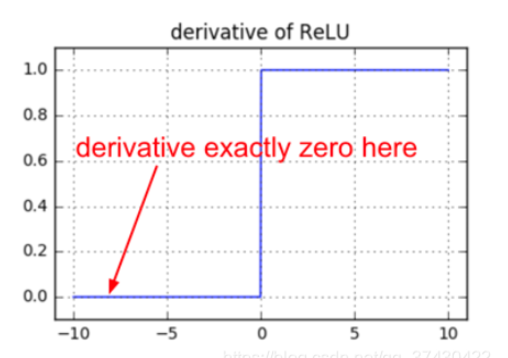
ReLU 的导数在正区域是1,在非正区域是0。
>>> import numpy
>>> x = [1, 2, 0, -6]
>>> z = np.maximum(0, np.dot(W, x))
>>> z
array([0, 5])
>>> z > 0
array([False, True])
>>> dz_dW = np.outer(z > 0, x)
array([[ 0, 0, 0, 0],
[ 1, 2, 0, -6]])
>>> x
[1, 2, 0, -6]
>>> W
[[1, 2, 1, 1], [1, 2, 3, 0]]
观察上述代码你会发现,当前向传递中一个神经元的值恒等于 0(即zi=0表示该神经元未被激活),该神经元对应的权重的梯度将为0,这时权重得不到更新。这就会导致所谓的“死亡”ReLU问题。

w用什么参数来更新 看z 如果z>0 则用输入x更新 如果z<0 则不用更新
如果一个ReLU 神经元由于被不恰当地初始化等于 0或是其对应的参数在训练过程中由于大幅度的更新而接近于 0(这时在下一样本的计算中该神经元的值就会趋于为 0,随着而来的是权重的梯度为 0,权重无法更新,导致该神经元的值恒为 0),那么这个神经元将永远处于死亡状态。这就是“死亡” ReLU。这就像是永恒的,无法恢复的大脑损伤。有时,你将整个训练数据集放入一个训练过的网络中进行前向计算,你可能会发现大部分(如 40% )的神经元的值一直恒为零。
所以,在使用 ReLUs 时,要警惕死亡ReLUs,这些神经元在整个训练数据集中任一样本中都不会被激活,而是处于死亡状态。神经元在训练过程中的“死亡”,通常是学习率过大造成的。
np.dot
np.dot(a, b) 得出的是一个标量
np.dot(A, v) 等价于 A @ v (@ 是 矩阵乘法运算符)
np.dot(A, B) 等价于 A @ B
np.outer
np.outer 函数用于计算两个向量的外积(outer product)。外积是两个向量之间的一种乘法,其结果是一个矩阵,而不是一个标量。
两个向量的叉乘,又叫向量积、外积、叉积,叉乘的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量组成的坐标平面垂直。
定义:如果 a 和 b 分别是长度为 m 和 n 的两个一维数组,那么 np.outer(a, b) 的结果是一个形状为 (m, n) 的矩阵 C,其中每个元素 C[i, j] = a[i] * b[j]。
如果 a = [1, 2] 和 b = [3, 4, 5],那么 np.outer(a, b) 将产生如下矩阵
[[3, 4, 5],
[6, 8, 10]]
np.outer 是 NumPy 提供的一个强大工具,特别适合用来创建基于两个向量的所有可能配对的product矩阵

