机器学习-无监督机器学习-图聚类-21
参考链接:https://www.cnblogs.com/pinard/p/6221564.html
1. AP聚类算法
affinity 相似度
propgaption 传播
exemplars 模范 代表
Affinity Propagation Clustering特别适合高维、多类数据快速聚类,相比传统的聚类算法,该算法算是比较新的,从聚类性能和效率方面都有大幅度的提升。
Affinity Propagation 通过数据点之间传递两种消息(responsibility and availability)直到收敛来创建聚类并更新
preference:参考度;它控制多少 exemplars样本 (orprototypes) 会成为聚类中心点
damping factor:它衰减消息的 responsibility and availability去避免数值振荡当更新这些消息时
AP算法运行前,构建一个相似度矩阵s,s就会是一个N*N矩阵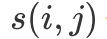
,代表Xi和Xj之间的相似度
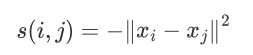
矩阵对角线上的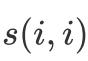
尤其重要,它代表了第i条数据的preference,意味着它有多大可能成为一个exemplar。这个值会和超参数比较,值越大,越有可能产生更多的类别;值越小,产生更
少的类别。
步骤:
算法初始,将responsibility矩阵R和availability矩阵A初始化为全0矩阵

更新吸引度矩阵
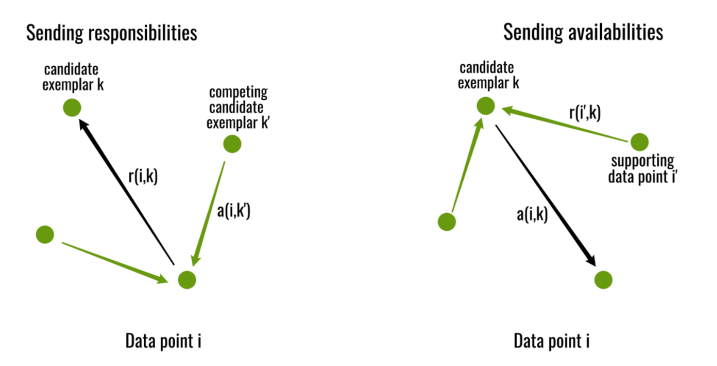
更新归属度矩阵
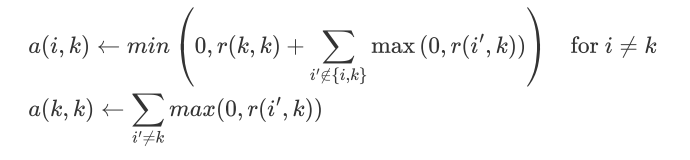
根据衰减系数 对两个值进行衰减
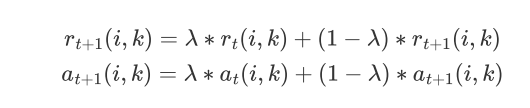
算法运行后
'responsibility'矩阵 + 'availability'矩阵 得到一个最终矩阵,exemplars从最终矩阵中抽取出来,就是那些数值上大于0的作为聚类中心,根据距离远近进行划分就
可以得到聚类结果了。
2. Spectral Clustering 谱聚类
把样本数据点看成是graph图里面的节点,并且把聚类问题转换成了graph图分割问题。
建立相似度Graph:
Graph由任意两点之间的权重值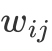
组成的矩阵,距离较远的两个点之间的边权重值较低,而距离较近的两个点之间的边权重值较高
邻接矩阵的构建方式:
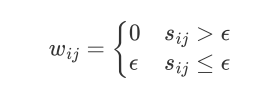
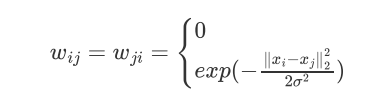
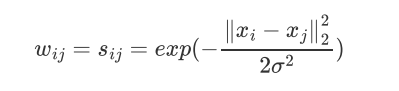
实际应用中,使用全连接法来建立邻接矩阵是最普遍的,而在全连接法中使用高斯径向核RBF是最普遍的。
降维:
同一个簇中的成员有可能在给定的维度空间里面相距很远。但是在降低的维度空间中离的更近,并且可以被传统聚类算法聚到一起,所以要降维
去计算Graph图的 Laplacian Matrix。
概念:
G(V,E) Graph图 V点的集合 E边的集合
对于图中的任意一个点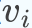
,它的度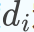
定义为和它相连的所有边的权重之和: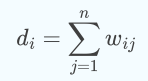
这样我们可以得到一个
的度矩阵D,描述的是每一个节点的度, 它是一个对角矩阵,只有主对角线有值。
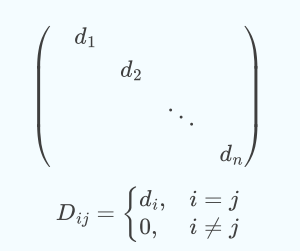
图的拉普拉斯矩阵被定义为: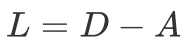
为了减少维度,首先,特征值和对应的特征向量被计算出来。如果聚类数为K,那么前面个k最小特征值和对应的特征向量被拿出来堆叠成一个矩阵,矩阵的列是这些特征向量。为了数学上的效率,这
个矩阵之后被归一化;
谱聚类本质--无向图切图
谱聚类是一种基于图的聚类方法,它是把数据集构成一张图,然后聚多少类就把图切成多少块
无向图G(V, E)切成互相没有连接的k个子图,
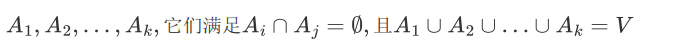
定义和 之间的切图权重为:
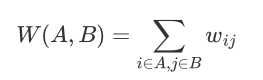
对于k个子图点的集合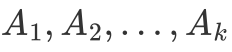
定义切图cut为:
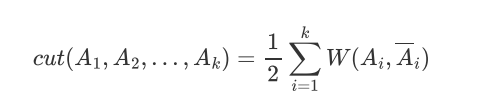
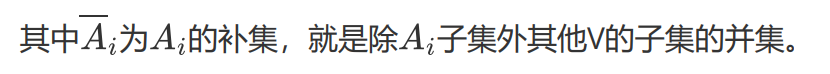
如何切图可以让子图内的点权重之和高,子图间的点权重之和低呢?
最下小化cut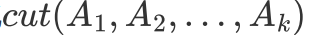 会导致如下问题:
会导致如下问题:
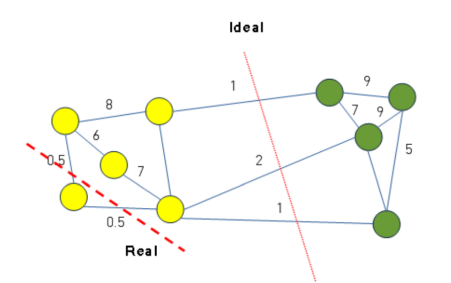
选择了一个权重最小的边缘的点进行cut,但是却不是最优的切图,如何避免这种切图,并且找到类似图中Ideal这样的最优切图呢?
RatioCut:
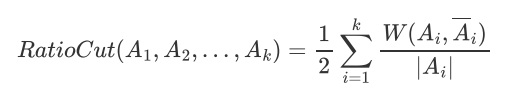
考虑最大化每个子图点的个数,让每个子图里面的点个数 尽可能的多。
指示向量:
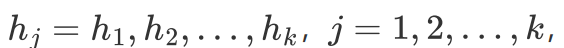
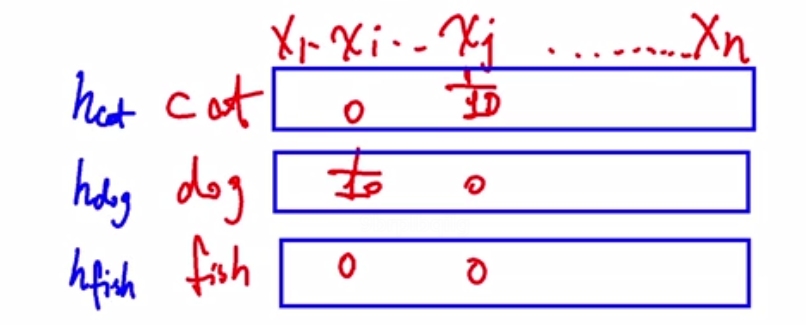
指示向量带入:
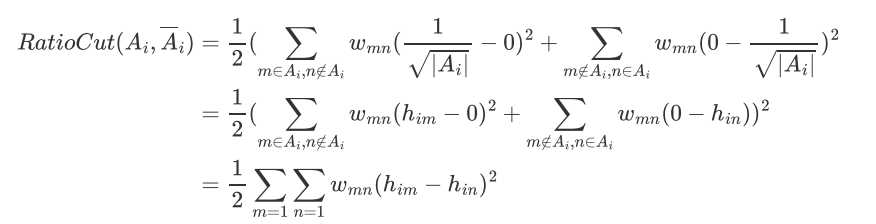
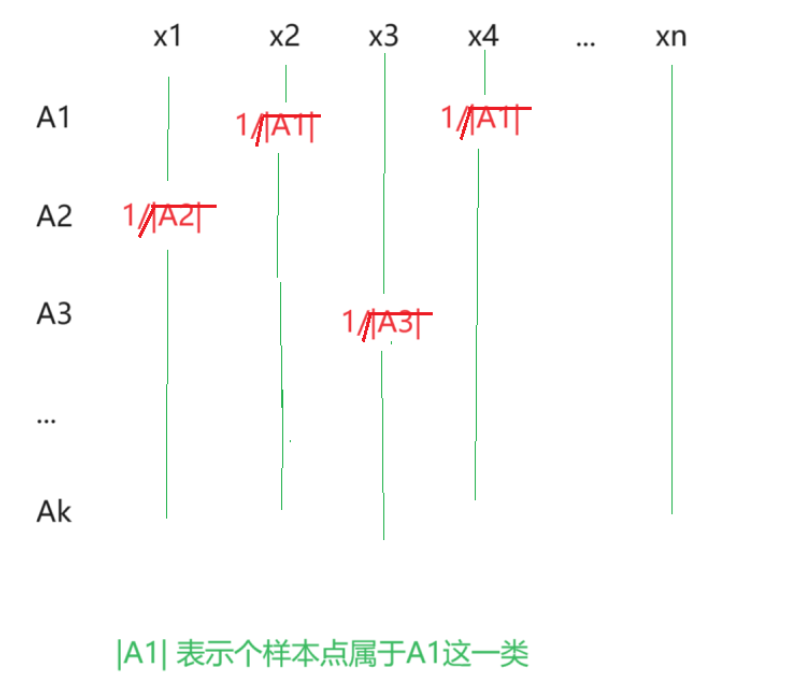
什么要带根号?带上根号之后 Ht*H 就会 = 1
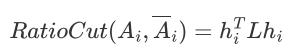
切成k个子图:

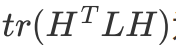
为矩阵的迹 trace,切图优化目标函数为:
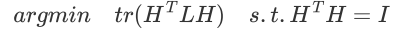
目标就是找到k个最小的特征值,通过找到L的最小的k个特征值,可以得到对应的k个特征向量,这k个特征向量组成一个n*k维度的矩阵,就是我们的H
Ncut切图:
由于子图样本个数多并不一定权重就大,我们切图时基于权重也更符合我们的目标,因此一般Ncut切图优于RatioCut切图
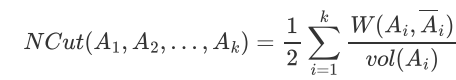
vol(Ai) 代表Ai子图里面所有边的权重总和
对应的指示向量也做相应的修改:
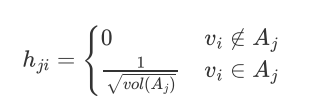
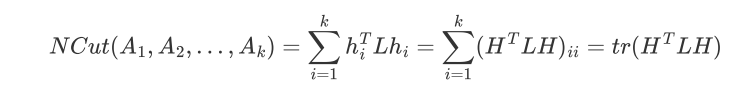
约束条件不一样:

令: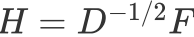
则: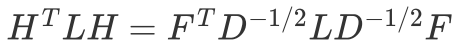
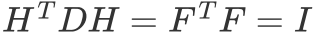
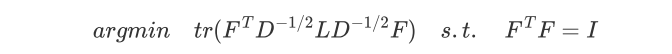
可以发现这个式子和RatioCut基本一致,只是中间的L变成了:
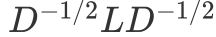
可以继续按照RatioCut的思想,求出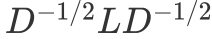
最小的前k个特征值

