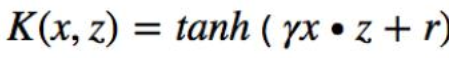机器学习-线性分类-支持向量机SVM-软间隔-核函数-13
1. 总结 SVM
SVM算法的基础是感知器模型,
感知器模型 与 逻辑回归的不同之处?
逻辑回归 sigmoid(θx) 映射到 0-1之间给出预测概率
感知器分类 sign(θx) 输出θx的符号, +1 或者-1 给出x是属于正样本还是负样本
直接输出 θx的值就是 线性回归
感知器 模型 只要能将寻找到这样的一个超平面 将正样本与负样本能够区分开来就行,
而SVM不仅要能区分 而且还要能使得 距离超平面最进的点 到达这样的一个超平面距离最大

这也就是一个 二次优化的问题, 先找最近的点,再通过这些最近的点,确定最终的超平面。
显然 SVM 具有比 感知器 更优的泛化能力
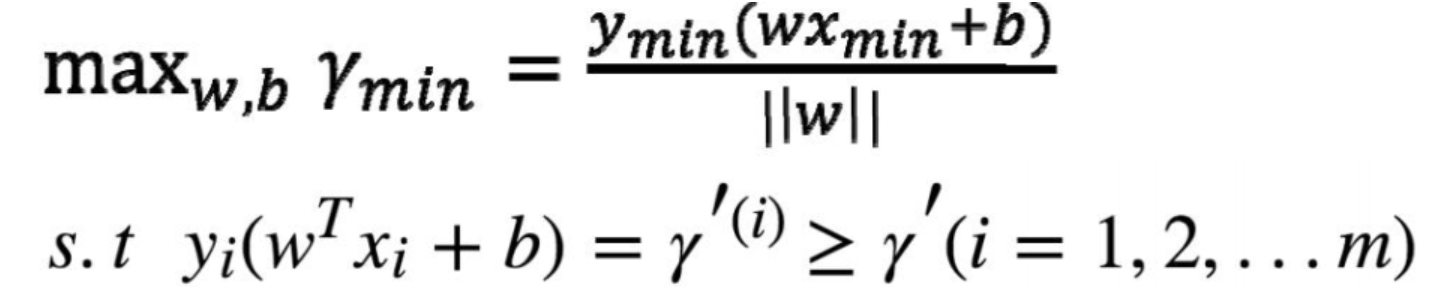
寻找这样的 模型参数 w b(也就是θ), 使得 最近的点 Xmin Ymin 到达 参数确定的的平面 距离尽可能的远,这样得到的参数θ 就是最终的完美的
仔细品味下这张图:

超平面的法向量 w 是方向的 通过W b 就能唯一确定一个平面
简单总结下:
求解W b 转化成 求解α*
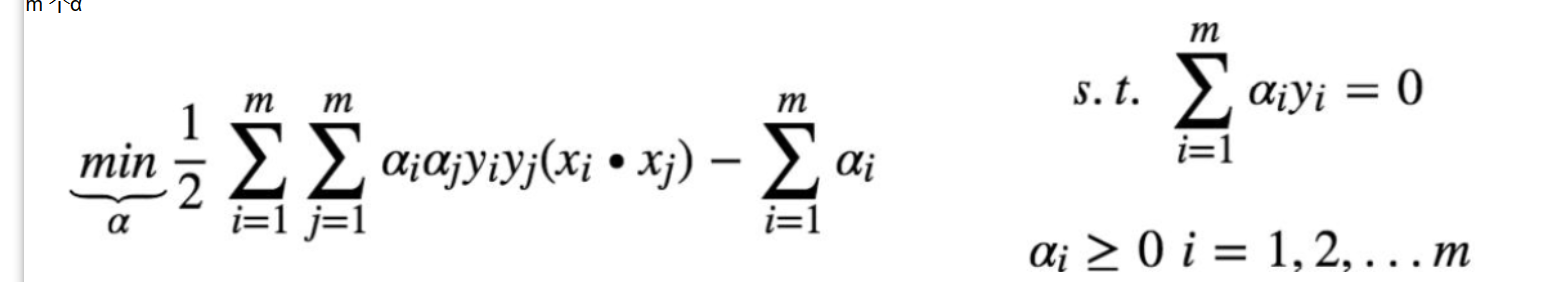
m条样本 就有m个α

α求得之后 可直接 求得W

通过那些不为0的α 带入后 可求得b 取平均 得到b
以上的求解 叫做 硬间隔SVM
下面讲解 软间隔svm
2. 软间隔svm
有些时候 噪声 会造成 线性 不可分
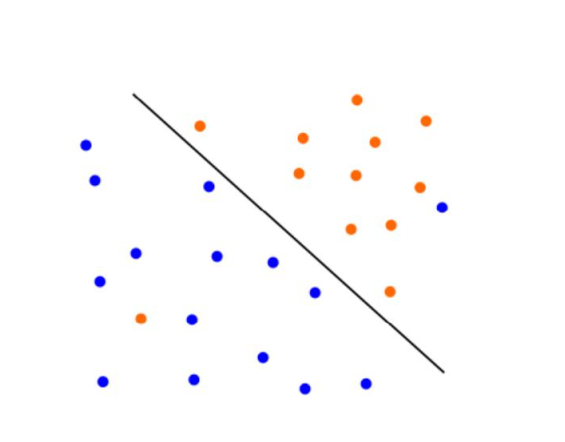
正样本 负样本 在边界处 相互渗透 这就导致 没法用 上面的SVM 意味着找不到一个合格的超平面
引入松弛变量 提出松弛变量ξi≥0(每个数据点自己有一个ξi)
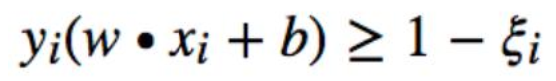
这样就至少肯定有好多的 w 和 b 满足条件了
ξ代表异常点嵌入间隔面的深度, 我们要在能选出符合约束条件的最好的 w 和 b 的同时,让
嵌入间隔面的总深度越少越好
问题转化成:
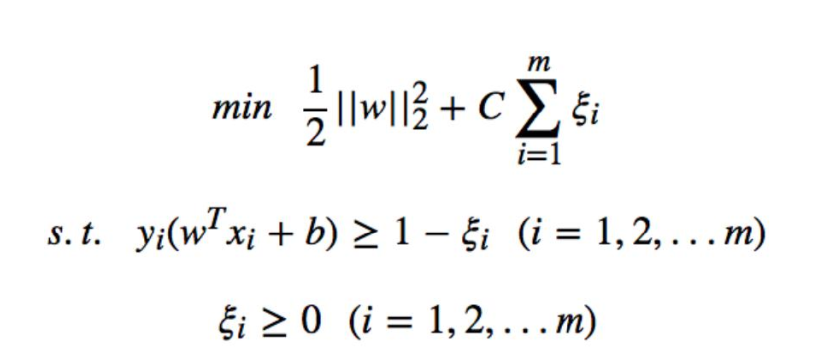
约束条件 变成了两个
构造拉格朗日函数:
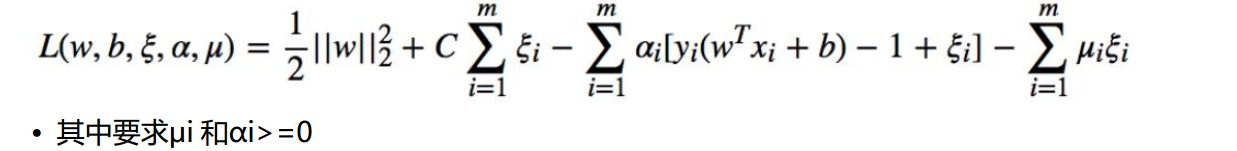

问题转化成对偶问题:
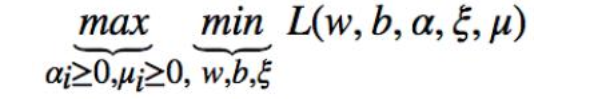
先求 L 函数对 w,b,ξ的极小值,再求其对α和μ的极大值
得到:

与硬间隔 SVM一样的表达式 只不过约束条件不一样
最终问题换成:

与之前相比,只是多了个约束条件而已,仍然可以使用 SMO 来求解
结论:

C是一个系数 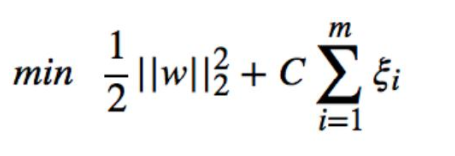
损失函数两部分更侧重于哪一部分
4. 核函数
线性 SVM 来说,判别函数为:
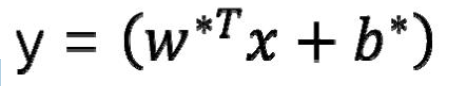
由于:
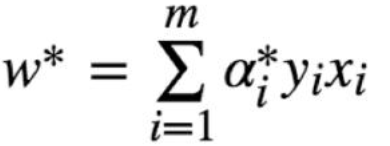
代入后得到:
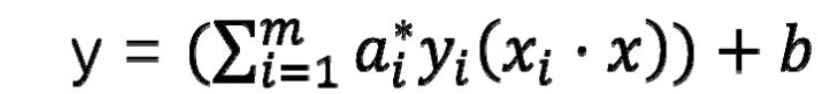
每一次在计算判别函数结果时需要求得待判断点和所有训练集样本点的內积 xi*x 这里铺垫一下对于升维 需要用到这个结果
升维是一种处理线性不可分问题的方式,我们通过把原始的 x 映射到更高维空间φ(x)上
比如多项式回归:可以将 2 元特征(x1,x2) 映射为 5 元特征(x1,x2,x1*x2,x12,x22) 这样在五元空间中有
些二元空间里线性不可分的问题就变得线性可分了
但是对于SVM如何做升维?
升维示意图:
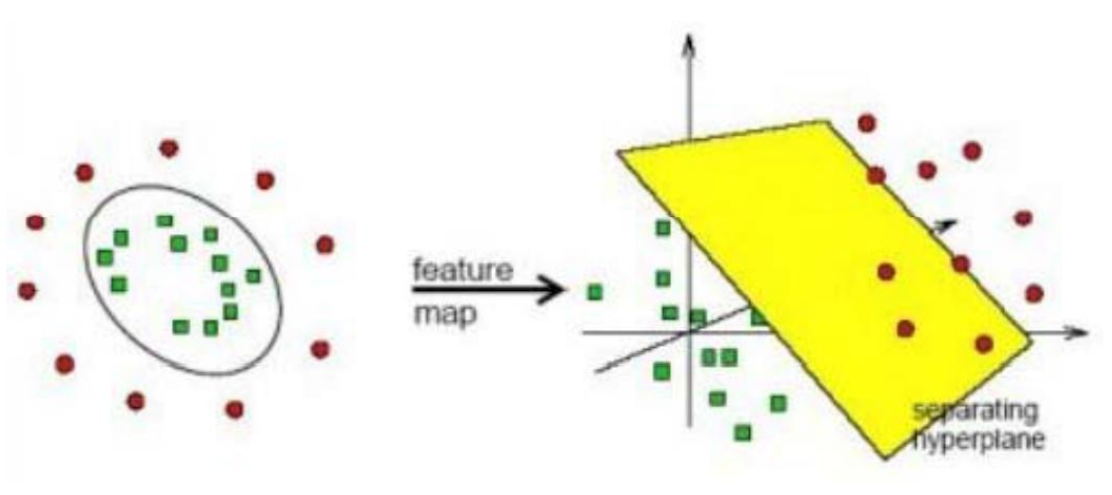
看似这种升维方式已经完美解决了线性不可分问题,但是带来了一个新问题
假设就使用多项式回归的方式进行升维:对于二维 x1,x2 升维后的结果是:
x1,x2,x1*x2,x12,x22
假如是三维数据 x1,x2,x3 呢?
19 维!升维之后还需要做向量的内积,时间空间消耗就更可怕了
低维度的计算 就能得到升维后的结果!!!
定义: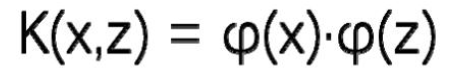
问题就转化成:
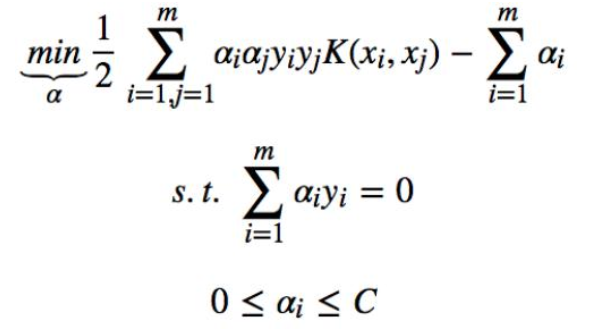
判别式转化成:
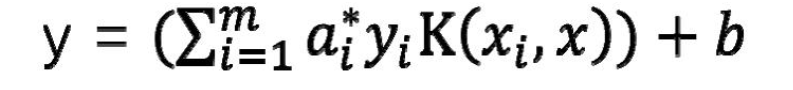
常用的核函数:
线性核函数: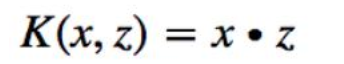
高斯核函数:
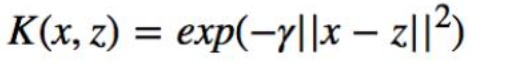
多项式核函数:
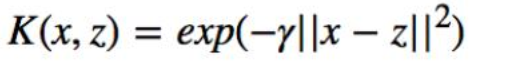
sigmoid核函数(-1, +1)之间的s型曲线 与逻辑回归的sigmoid(0,1)不同而已: