G4、CGAN|生成手势图像——可控制生成
- 🍨 本文为🔗365天深度学习训练营 中的学习记录博客
- 🍖 原作者:K同学啊
- 🚀 文章来源:K同学的学习圈子
本周任务:
📌 基础任务:
- 结合代码进一步了解CGAN
- 学习如何运用生成好的生成器生成指定图像
一、理论基础¶
1、DCGAN原理¶
条件生成对抗网络(CGAN)是在生成对抗网络(GAN)的基础上进行了一些改进。对于原始GAN的生成器而言,其生成的图像数据是随机不可预测的,因此我们无法控制网络的输出,在实际操作中的可控性不强。
针对上述原始GAN无法生成具有特定属性的图像数据的问题,Mehdi Mirza等人在2014年提出了条件生成对抗网络(CGAN),全称为Conditional Generative Adversarial Network。与标准的 GAN 不同,CGAN 通过给定额外的条件信息来控制生成的样本的特征。这个条件信息可以是任何类型的,例如图像标签、文本标签等。
在 CGAN 中,生成器(Generator)和判别器(Discriminator)都接收条件信息。生成器的目标是生成与条件信息相关的合成样本,而判别器的目标是将生成的样本与真实样本区分开来。当生成器和判别器通过反馈循环不断地进行训练时,生成器会逐渐学会如何生成符合条件信息的样本,而判别器则会逐渐变得更加准确。
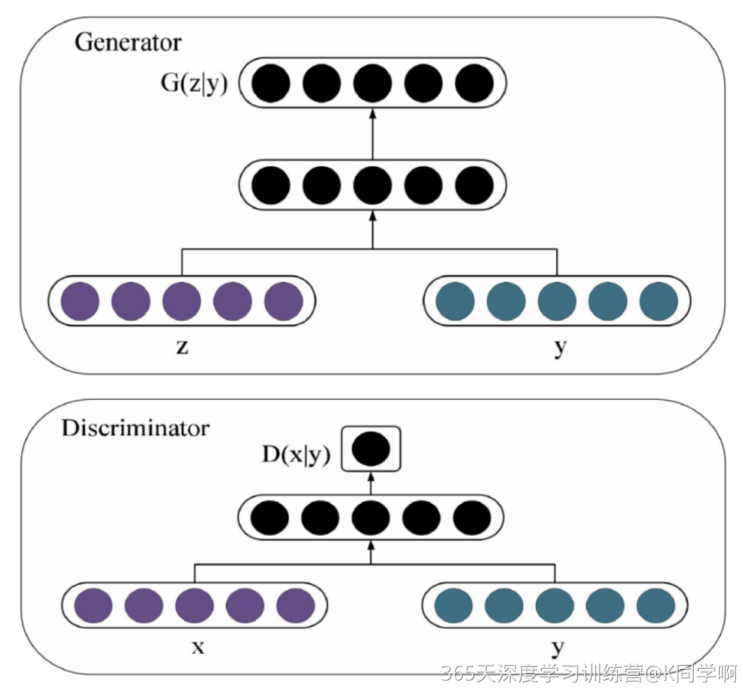
由上图的网络结构可知,条件信息y作为额外的输入被引入对抗网络中,与生成器中的噪声z合并作为隐含层表达;而在判别器D中,条件信息y则与原始数据x合并作为判别函数的输入。
二、准备工作¶
数据:百度网盘
1、导入包¶
import torch
import numpy as np
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
from torch.autograd import Variable
from torchvision.utils import save_image
from torchvision.utils import make_grid
from torch.utils.tensorboard import SummaryWriter
from torchsummary import summary
import matplotlib.pyplot as plt2、设置超参数¶
dataroot = "./data/GAN-3-day-rps/" # 数据路径
batch_size = 128 # 训练过程中的批次大小
image_size = 128 # 图像的尺寸(宽度和高度)
image_shape = (3, 128, 128)
image_dim = int(np.prod(image_shape))
latent_dim = 100
n_classes = 3 # 条件标签的总数
embedding_dim = 100
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')3、导入数据¶
- 首先使用ImageFolder类创建一个数据集对象,该对象表示从文件夹中加载的图像数据集
- 然后,通过transforms.Compose组合了一系列图像变换操作来对图像进行预处理,包括调整大小、中心裁剪、转换为张量以及标准化
- 接着,使用DataLoader类创建一个数据加载器对象,该对象可以在训练过程中按批次加载数据,并可以选择是否打乱数据集以及使用多线程加载数据。代码还选择设备(GPU或CPU)来运行代码,并显示所选择的设备
- 最后,代码通过数据加载器获取一批训练图像,并使用Matplotlib库绘制这些图像
解决一个小问题,关于路径图像读取的,图像实际的目录为./data/GAN-Data/FaceSample,而将数据集路径定为上一级目录 "./data/GAN-Data",是因为PyTorch支持自动扫描指定目录下的所有子目录,以发现数据集文件。使用 torchvision.datasets.ImageFolder 类来读取数据集。此时,你只需要将数据集路径定为 "./data/GAN-Data" 即可,因为 ImageFolder 类会自动扫描该目录下的所有子目录,以发现数据集文件。如果目录下有多个不同的文件夹,ImageFolder 类会将每个文件夹名作为一个标签类别,并将文件夹中的所有图像文件都视为该类别下的样本。如果数据集目录 "./data/GAN-Data",其中包含三个子目录 "cats"、"dogs" 和 "pandas",每个子目录下都包含对应的图像文件。ImageFolder 类将读取 "./data/GAN-Data" 目录下的所有子目录,并将每个子目录名作为一个标签类别。
# 创建数据集
train_dataset = datasets.ImageFolder(root=dataroot,
transform=transforms.Compose([
transforms.Resize(image_size), # 调整图像大小
transforms.ToTensor(), # 将图像转换为张量
transforms.Normalize((0.5, 0.5, 0.5), # 标准化图像张量
(0.5, 0.5, 0.5)),
]))
# 创建数据加载器
train_loader = torch.utils.data.DataLoader(train_dataset,
batch_size=batch_size, # 批量大小
shuffle=True, # 是否打乱数据集
num_workers=6 # 使用多个线程加载数据的工作进程数
)4、数据可视化¶
关于ax.imshow(make_grid(images.detach(), nrow=22).permute(1, 2, 0))详解:
- ax: 这是一个matplotlib的轴对象(axis),用于在图形上放置图像。通常,它用于创建子图。
- make_grid(images.detach(), nrow=10): 这是一个函数调用。make_grid函数的作用是将一组图像拼接成一个网格。它接受两个参数:images和nrow。images是一个包含图像的张量,nrow是可选参数,表示每行显示的图像数量。在这里,它将图像进行拼接,并设置每行显示10个图像。
- permute(1, 2, 0): 这是一个张量的操作,用于交换维度的顺序。在这里,对于一个3维的张量(假设图像维度为(C,H,W),其中C是通道数,H是高度,W是宽度),permute(1, 2, 0)将把通道维度(C)移动到最后,而将高度和宽度维度(H,W)放在前面。这样做是为了符合matplotlib对图像的要求,因为matplotlib要求图像的维度为(H,W,C)。
- imshow(...): 这是matplotlib的一个函数,用于显示图像。在这里,它接受一个拼接好并且维度已经调整好的图像张量,并将其显示在之前创建的轴对象(ax)上。
def show_images(images):
fig, ax = plt.subplots(figsize=(20, 20))
ax.set_xticks([]); ax.set_yticks([])
ax.imshow(make_grid(images.detach(), nrow=22).permute(1, 2, 0))
def show_batch(dl):
for images, _ in dl:
show_images(images)
break
show_batch(train_loader)Clipping input data to the valid range for imshow with RGB data ([0..1] for floats or [0..255] for integers).
# 自定义权重初始化函数,用于初始化生成器和判别器的权重
def weights_init(m):
# 获取当前层的类名
classname = m.__class__.__name__
# 如果当前层是卷积层(类名中包含 'Conv' )
if classname.find('Conv') != -1:
# 使用正态分布随机初始化权重,均值为0,标准差为0.02
torch.nn.init.normal_(m.weight, 0.0, 0.02)
# 如果当前层是批归一化层(类名中包含 'BatchNorm' )
elif classname.find('BatchNorm') != -1:
# 使用正态分布随机初始化权重,均值为1,标准差为0.02
torch.nn.init.normal_(m.weight, 1.0, 0.02)
# 将偏置项初始化为全零
torch.nn.init.zeros_(m.bias)2、定义生成器¶
- label_conditioned_generator:Sequential 模型,用于将条件标签映射到嵌入空间中
nn.Embedding 用于将条件标签映射为稠密向量,nn.Linear 用于将稠密向量转换为更高维度
- latent: Sequential 模型,用于将噪声向量映射到图像空间中
nn.Linear 用于将潜在向量转换为更高维度,nn.LeakyReLU 用于进行非线性映射
- model: Sequential 模型,用于将条件标签和潜在向量合并成生成的图像
nn.ConvTranspose2d 表示反卷积操作,用于将特征图映射为图像。nn.BatchNorm2d 表示批标准化,用于提高模型的稳定性和收敛速度。nn.ReLU 表示 ReLU 激活函数,用于进行非线性映射。nn.Tanh 表示 Tanh 激活函数,用于将生成的图像像素值映射到 [-1, 1] 范围内
- forward 方法,用于前向传播计算
inputs 是一个元组,包含两个张量:noise_vector 表示噪声向量,label 表示条件标签。在 forward 方法中,先通过 label_conditioned_generator 将 label 映射为嵌入向量,再通过 latent 将 noise_vector 映射为潜在向量。然后,将嵌入向量和潜在向量在通道维度上进行合并,得到合并后的特征图。最后,通过 model 将特征图生成为 RGB 图像
- 将生成器模型实例化为 generator,并对其权重进行初始化
weights_init 是一个函数,用于初始化模型权重
class Generator(nn.Module):
def __init__(self):
super(Generator, self).__init__()
# 定义条件标签的生成器部分,用于将标签映射到嵌入空间中
# n_classes:条件标签的总数
# embedding_dim:嵌入空间的维度
self.label_conditioned_generator = nn.Sequential(
nn.Embedding(n_classes, embedding_dim), # 使用Embedding层将条件标签映射为稠密向量
nn.Linear(embedding_dim, 16) # 使用线性层将稠密向量转换为更高维度
)
# 定义潜在向量的生成器部分,用于将噪声向量映射到图像空间中
# latent_dim:潜在向量的维度
self.latent = nn.Sequential(
nn.Linear(latent_dim, 4*4*512), # 使用线性层将潜在向量转换为更高维度
nn.LeakyReLU(0.2, inplace=True) # 使用LeakyReLU激活函数进行非线性映射
)
# 定义生成器的主要结构,将条件标签和潜在向量合并成生成的图像
self.model = nn.Sequential(
# 反卷积层1:将合并后的向量映射为64x8x8的特征图
nn.ConvTranspose2d(513, 64*8, 4, 2, 1, bias=False),
nn.BatchNorm2d(64*8, momentum=0.1, eps=0.8), # 批标准化
nn.ReLU(True), # ReLU激活函数
# 反卷积层2:将64x8x8的特征图映射为64x4x4的特征图
nn.ConvTranspose2d(64*8, 64*4, 4, 2, 1, bias=False),
nn.BatchNorm2d(64*4, momentum=0.1, eps=0.8),
nn.ReLU(True),
# 反卷积层3:将64x4x4的特征图映射为64x2x2的特征图
nn.ConvTranspose2d(64*4, 64*2, 4, 2, 1, bias=False),
nn.BatchNorm2d(64*2, momentum=0.1, eps=0.8),
nn.ReLU(True),
# 反卷积层4:将64x2x2的特征图映射为64x1x1的特征图
nn.ConvTranspose2d(64*2, 64*1, 4, 2, 1, bias=False),
nn.BatchNorm2d(64*1, momentum=0.1, eps=0.8),
nn.ReLU(True),
# 反卷积层5:将64x1x1的特征图映射为3x64x64的RGB图像
nn.ConvTranspose2d(64*1, 3, 4, 2, 1, bias=False),
nn.Tanh() # 使用Tanh激活函数将生成的图像像素值映射到[-1, 1]范围内
)
def forward(self, inputs):
noise_vector, label = inputs
# 通过条件标签生成器将标签映射为嵌入向量
label_output = self.label_conditioned_generator(label)
# 将嵌入向量的形状变为(batch_size, 1, 4, 4),以便与潜在向量进行合并
label_output = label_output.view(-1, 1, 4, 4)
# 通过潜在向量生成器将噪声向量映射为潜在向量
latent_output = self.latent(noise_vector)
# 将潜在向量的形状变为(batch_size, 512, 4, 4),以便与条件标签进行合并
latent_output = latent_output.view(-1, 512, 4, 4)
# 将条件标签和潜在向量在通道维度上进行合并,得到合并后的特征图
concat = torch.cat((latent_output, label_output), dim=1)
# 通过生成器的主要结构将合并后的特征图生成为RGB图像
image = self.model(concat)
return image
generator = Generator().to(device)
generator.apply(weights_init)
print(generator)Generator(
(label_conditioned_generator): Sequential(
(0): Embedding(3, 100)
(1): Linear(in_features=100, out_features=16, bias=True)
)
(latent): Sequential(
(0): Linear(in_features=100, out_features=8192, bias=True)
(1): LeakyReLU(negative_slope=0.2, inplace=True)
)
(model): Sequential(
(0): ConvTranspose2d(513, 512, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(1): BatchNorm2d(512, eps=0.8, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): ConvTranspose2d(512, 256, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(4): BatchNorm2d(256, eps=0.8, momentum=0.1, affine=True, track_running_stats=True)
(5): ReLU(inplace=True)
(6): ConvTranspose2d(256, 128, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(7): BatchNorm2d(128, eps=0.8, momentum=0.1, affine=True, track_running_stats=True)
(8): ReLU(inplace=True)
(9): ConvTranspose2d(128, 64, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(10): BatchNorm2d(64, eps=0.8, momentum=0.1, affine=True, track_running_stats=True)
(11): ReLU(inplace=True)
(12): ConvTranspose2d(64, 3, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(13): Tanh()
)
)查看模型参数
from torchinfo import summary
summary(generator)=================================================================
Layer (type:depth-idx) Param #
=================================================================
Generator --
├─Sequential: 1-1 --
│ └─Embedding: 2-1 300
│ └─Linear: 2-2 1,616
├─Sequential: 1-2 --
│ └─Linear: 2-3 827,392
│ └─LeakyReLU: 2-4 --
├─Sequential: 1-3 --
│ └─ConvTranspose2d: 2-5 4,202,496
│ └─BatchNorm2d: 2-6 1,024
│ └─ReLU: 2-7 --
│ └─ConvTranspose2d: 2-8 2,097,152
│ └─BatchNorm2d: 2-9 512
│ └─ReLU: 2-10 --
│ └─ConvTranspose2d: 2-11 524,288
│ └─BatchNorm2d: 2-12 256
│ └─ReLU: 2-13 --
│ └─ConvTranspose2d: 2-14 131,072
│ └─BatchNorm2d: 2-15 128
│ └─ReLU: 2-16 --
│ └─ConvTranspose2d: 2-17 3,072
│ └─Tanh: 2-18 --
=================================================================
Total params: 7,789,308
Trainable params: 7,789,308
Non-trainable params: 0
=================================================================# 定义了两个张量 a 和 b,分别表示噪声向量和条件标签
# 其中,a 的形状为 (100,),b 的形状为 (1,)
# 由于生成器模型需要的条件标签是一个整数,因此需要将 b 的数据类型转换为 long
# 最后,将 a 和 b 分别转移到 GPU 上,以便在 GPU 上进行模型计算
a = torch.ones(100)
b = torch.ones(1)
b = b.long()
a = a.to(device)
b = b.to(device)
generator((a,b))tensor([[[[-1.8915e-03, 1.2908e-04, -3.1682e-03, ..., 2.0741e-03,
-2.6199e-03, -2.0648e-03],
[-2.8762e-03, 1.5156e-03, -2.0248e-03, ..., -4.0703e-04,
-5.6482e-03, -1.1544e-03],
[-2.4234e-03, -1.1187e-03, -2.4653e-03, ..., 8.9986e-05,
6.1591e-04, 1.2889e-03],
...,
[-3.8914e-03, -6.9504e-04, -1.3576e-03, ..., -1.0558e-03,
-5.6537e-03, -2.7072e-03],
[-1.7631e-03, -4.5605e-03, -3.1415e-03, ..., -1.3835e-03,
-2.1803e-03, -1.1289e-03],
[-3.2794e-04, -5.5474e-04, -3.8886e-03, ..., -3.1929e-04,
-3.8605e-03, -3.9521e-04]],
[[ 1.2093e-03, -7.6252e-04, 1.3181e-03, ..., 1.1522e-03,
1.6209e-03, -4.1160e-04],
[ 3.8540e-03, 4.7066e-04, 3.1471e-03, ..., -1.2243e-03,
2.6031e-03, -2.4856e-03],
[ 1.4104e-03, -2.7886e-04, -5.3110e-05, ..., 6.2734e-03,
2.7215e-03, 1.0710e-03],
...,
[ 2.9601e-03, -1.5062e-03, 7.0235e-04, ..., -8.3861e-04,
3.7338e-03, -5.7328e-04],
[ 2.3218e-03, 1.9503e-03, 1.4642e-03, ..., -7.6540e-05,
4.8674e-03, -9.0718e-04],
[ 1.4450e-03, -1.2534e-03, 1.9311e-03, ..., 1.2226e-03,
9.0703e-04, -9.4872e-04]],
[[-4.7044e-04, -6.5240e-04, 3.3990e-04, ..., 5.1420e-04,
7.6714e-04, -1.2788e-04],
[-5.5303e-04, 4.7669e-04, -1.3567e-04, ..., -2.4559e-04,
-4.5241e-03, -2.1225e-04],
[-2.6251e-03, -2.2154e-03, 3.0092e-03, ..., 2.0665e-03,
9.3912e-04, -3.6619e-03],
...,
[-1.2418e-03, -9.9028e-04, -1.7181e-03, ..., -9.8700e-04,
-2.2857e-03, 6.7540e-04],
[-1.7132e-03, 5.5081e-04, 1.1504e-03, ..., 3.5673e-03,
1.4379e-03, -4.1137e-03],
[-7.4285e-04, -1.0870e-03, -1.7262e-03, ..., -7.5150e-04,
-1.2525e-03, -5.5326e-04]]]], device='cuda:0',
grad_fn=<TanhBackward0>)3、定义鉴别器¶
- label_condition_disc:条件标签的嵌入层,用于将类别标签转换为特征向量
这个嵌入层由两个层组成:一个嵌入层(Embedding)和一个线性层(Linear)。嵌入层将类别标签编码为固定长度的向量,线性层将嵌入的向量转换为与图像尺寸相匹配的特征张量。
- model:Sequential 模型
由多个卷积层、批量归一化层、激活函数层、展平层、随机失活层和全连接层组成。这些层将特征图逐渐变小,最后输出一个维度为1的概率值,表示输入的图像是真实的还是伪造的
- forward方法中,接受了一个inputs参数,其中包含了图像和标签两个部分
首先将标签通过条件标签的嵌入层转换为特征向量,然后通过重塑操作将特征向量转换为与图像尺寸相匹配的特征张量
接下来将图像和标签特征拼接在一起作为鉴别器的输入,通过鉴别器模型进行前向传播,得到输出结果
class Discriminator(nn.Module):
def __init__(self):
super(Discriminator, self).__init__()
# 定义一个条件标签的嵌入层,用于将类别标签转换为特征向量
self.label_condition_disc = nn.Sequential(
nn.Embedding(n_classes, embedding_dim), # 嵌入层将类别标签编码为固定长度的向量
nn.Linear(embedding_dim, 3*128*128) # 线性层将嵌入的向量转换为与图像尺寸相匹配的特征张量
)
# 定义主要的鉴别器模型
self.model = nn.Sequential(
nn.Conv2d(6, 64, 4, 2, 1, bias=False), # 输入通道为6(包含图像和标签的通道数),输出通道为64,4x4的卷积核,步长为2,padding为1
nn.LeakyReLU(0.2, inplace=True), # LeakyReLU激活函数,带有负斜率,增加模型对输入中的负值的感知能力
nn.Conv2d(64, 64*2, 4, 3, 2, bias=False), # 输入通道为64,输出通道为64*2,4x4的卷积核,步长为3,padding为2
nn.BatchNorm2d(64*2, momentum=0.1, eps=0.8), # 批量归一化层,有利于训练稳定性和收敛速度
nn.LeakyReLU(0.2, inplace=True),
nn.Conv2d(64*2, 64*4, 4, 3, 2, bias=False), # 输入通道为64*2,输出通道为64*4,4x4的卷积核,步长为3,padding为2
nn.BatchNorm2d(64*4, momentum=0.1, eps=0.8),
nn.LeakyReLU(0.2, inplace=True),
nn.Conv2d(64*4, 64*8, 4, 3, 2, bias=False), # 输入通道为64*4,输出通道为64*8,4x4的卷积核,步长为3,padding为2
nn.BatchNorm2d(64*8, momentum=0.1, eps=0.8),
nn.LeakyReLU(0.2, inplace=True),
nn.Flatten(), # 将特征图展平为一维向量,用于后续全连接层处理
nn.Dropout(0.4), # 随机失活层,用于减少过拟合风险
nn.Linear(4608, 1), # 全连接层,将特征向量映射到输出维度为1的向量
nn.Sigmoid() # Sigmoid激活函数,用于输出范围限制在0到1之间的概率值
)
def forward(self, inputs):
img, label = inputs
# 将类别标签转换为特征向量
label_output = self.label_condition_disc(label)
# 重塑特征向量为与图像尺寸相匹配的特征张量
label_output = label_output.view(-1, 3, 128, 128)
# 将图像特征和标签特征拼接在一起作为鉴别器的输入
concat = torch.cat((img, label_output), dim=1)
# 将拼接后的输入通过鉴别器模型进行前向传播,得到输出结果
output = self.model(concat)
return output
discriminator = Discriminator().to(device)
discriminator.apply(weights_init)
print(discriminator)Discriminator(
(label_condition_disc): Sequential(
(0): Embedding(3, 100)
(1): Linear(in_features=100, out_features=49152, bias=True)
)
(model): Sequential(
(0): Conv2d(6, 64, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(1): LeakyReLU(negative_slope=0.2, inplace=True)
(2): Conv2d(64, 128, kernel_size=(4, 4), stride=(3, 3), padding=(2, 2), bias=False)
(3): BatchNorm2d(128, eps=0.8, momentum=0.1, affine=True, track_running_stats=True)
(4): LeakyReLU(negative_slope=0.2, inplace=True)
(5): Conv2d(128, 256, kernel_size=(4, 4), stride=(3, 3), padding=(2, 2), bias=False)
(6): BatchNorm2d(256, eps=0.8, momentum=0.1, affine=True, track_running_stats=True)
(7): LeakyReLU(negative_slope=0.2, inplace=True)
(8): Conv2d(256, 512, kernel_size=(4, 4), stride=(3, 3), padding=(2, 2), bias=False)
(9): BatchNorm2d(512, eps=0.8, momentum=0.1, affine=True, track_running_stats=True)
(10): LeakyReLU(negative_slope=0.2, inplace=True)
(11): Flatten(start_dim=1, end_dim=-1)
(12): Dropout(p=0.4, inplace=False)
(13): Linear(in_features=4608, out_features=1, bias=True)
(14): Sigmoid()
)
)查看模型参数
summary(discriminator)=================================================================
Layer (type:depth-idx) Param #
=================================================================
Discriminator --
├─Sequential: 1-1 --
│ └─Embedding: 2-1 300
│ └─Linear: 2-2 4,964,352
├─Sequential: 1-2 --
│ └─Conv2d: 2-3 6,144
│ └─LeakyReLU: 2-4 --
│ └─Conv2d: 2-5 131,072
│ └─BatchNorm2d: 2-6 256
│ └─LeakyReLU: 2-7 --
│ └─Conv2d: 2-8 524,288
│ └─BatchNorm2d: 2-9 512
│ └─LeakyReLU: 2-10 --
│ └─Conv2d: 2-11 2,097,152
│ └─BatchNorm2d: 2-12 1,024
│ └─LeakyReLU: 2-13 --
│ └─Flatten: 2-14 --
│ └─Dropout: 2-15 --
│ └─Linear: 2-16 4,609
│ └─Sigmoid: 2-17 --
=================================================================
Total params: 7,729,709
Trainable params: 7,729,709
Non-trainable params: 0
=================================================================a = torch.ones(2,3,128,128) # 创建大小为2x3x128x128的张量a,元素值都为1
b = torch.ones(2,1) # 创建大小为2x1的张量b,元素值都为1
b = b.long() # 将张量b的数据类型转换为long型
a = a.to(device) # 将张量a移动到指定的设备上
b = b.to(device) # 将张量b移动到指定的设备上
c = discriminator((a,b)) # 对a和b进行前向传播,得到输出结果
c.size() # 打印输出结果c的大小torch.Size([2, 1])adversarial_loss = nn.BCELoss()
def generator_loss(fake_output, label):
gen_loss = adversarial_loss(fake_output, label)
return gen_loss
def discriminator_loss(output, label):
disc_loss = adversarial_loss(output, label)
return disc_loss2、定义优化器¶
learning_rate = 0.0002
G_optimizer = optim.Adam(generator.parameters(), lr = learning_rate, betas=(0.5, 0.999))
D_optimizer = optim.Adam(discriminator.parameters(), lr = learning_rate, betas=(0.5, 0.999))3、训练模型¶
这段代码是用于训练GAN模型生成图像的
- 首先设置了训练的总轮数和用于存储每轮训练中判别器和生成器损失的列表
- 然后进行GAN模型的训练。在每轮训练中,它首先从数据加载器中加载真实图像和标签,然后计算判别器对真实图像的损失,接着从噪声向量中生成假图像,计算判别器对假图像的损失,计算判别器总体损失并反向传播更新判别器的参数,然后计算生成器的损失并反向传播更新生成器的参数
- 最后,它打印当前轮次的判别器和生成器的平均损失,并将当前轮次的判别器和生成器的平均损失保存到列表中
- 在每10轮训练后,它会将生成的假图像保存为图片文件,并将当前轮次的生成器和判别器的权重保存到文件
# 设置训练的总轮数
num_epochs = 300
# 初始化用于存储每轮训练中判别器和生成器损失的列表
D_loss_plot, G_loss_plot = [], []
# 循环进行训练
for epoch in range(1, num_epochs + 1):
# 初始化每轮训练中判别器和生成器损失的临时列表
D_loss_list, G_loss_list = [], []
# 遍历训练数据加载器中的数据
for index, (real_images, labels) in enumerate(train_loader):
# 清空判别器的梯度缓存
D_optimizer.zero_grad()
# 将真实图像数据和标签转移到GPU(如果可用)
real_images = real_images.to(device)
labels = labels.to(device)
# 将标签的形状从一维向量转换为二维张量(用于后续计算)
labels = labels.unsqueeze(1).long()
# 创建真实目标和虚假目标的张量(用于判别器损失函数)
real_target = Variable(torch.ones(real_images.size(0), 1).to(device))
fake_target = Variable(torch.zeros(real_images.size(0), 1).to(device))
# 计算判别器对真实图像的损失
D_real_loss = discriminator_loss(discriminator((real_images, labels)), real_target)
# 从噪声向量中生成假图像(生成器的输入)
noise_vector = torch.randn(real_images.size(0), latent_dim, device=device)
noise_vector = noise_vector.to(device)
generated_image = generator((noise_vector, labels))
# 计算判别器对假图像的损失(注意detach()函数用于分离生成器梯度计算图)
output = discriminator((generated_image.detach(), labels))
D_fake_loss = discriminator_loss(output, fake_target)
# 计算判别器总体损失(真实图像损失和假图像损失的平均值)
D_total_loss = (D_real_loss + D_fake_loss) / 2
D_loss_list.append(D_total_loss)
# 反向传播更新判别器的参数
D_total_loss.backward()
D_optimizer.step()
# 清空生成器的梯度缓存
G_optimizer.zero_grad()
# 计算生成器的损失
G_loss = generator_loss(discriminator((generated_image, labels)), real_target)
G_loss_list.append(G_loss)
# 反向传播更新生成器的参数
G_loss.backward()
G_optimizer.step()
# 打印当前轮次的判别器和生成器的平均损失
print('Epoch: [%d/%d]: D_loss: %.3f, G_loss: %.3f' % (
(epoch), num_epochs, torch.mean(torch.FloatTensor(D_loss_list)),
torch.mean(torch.FloatTensor(G_loss_list))))
# 将当前轮次的判别器和生成器的平均损失保存到列表中
D_loss_plot.append(torch.mean(torch.FloatTensor(D_loss_list)))
G_loss_plot.append(torch.mean(torch.FloatTensor(G_loss_list)))
if epoch%10 == 0:
# 将生成的假图像保存为图片文件
save_image(generated_image.data[:50], './data/images_GAN3/sample_%d' % epoch + '.png', nrow=5, normalize=True)
# 将当前轮次的生成器和判别器的权重保存到文件
torch.save(generator.state_dict(), './training_weights/generator_epoch_%d.pth' % (epoch))
torch.save(discriminator.state_dict(), './training_weights/discriminator_epoch_%d.pth' % (epoch))Epoch: [1/300]: D_loss: 0.332, G_loss: 1.488
Epoch: [2/300]: D_loss: 0.263, G_loss: 2.501
Epoch: [3/300]: D_loss: 0.257, G_loss: 2.266
Epoch: [4/300]: D_loss: 0.320, G_loss: 2.083
Epoch: [5/300]: D_loss: 0.289, G_loss: 2.077
Epoch: [6/300]: D_loss: 0.492, G_loss: 2.085
Epoch: [7/300]: D_loss: 0.445, G_loss: 1.797
Epoch: [8/300]: D_loss: 0.450, G_loss: 1.556
Epoch: [9/300]: D_loss: 0.473, G_loss: 1.594
Epoch: [10/300]: D_loss: 0.475, G_loss: 1.569
Epoch: [11/300]: D_loss: 0.488, G_loss: 1.793
Epoch: [12/300]: D_loss: 0.514, G_loss: 1.663
Epoch: [13/300]: D_loss: 0.520, G_loss: 1.658
Epoch: [14/300]: D_loss: 0.451, G_loss: 1.631
Epoch: [15/300]: D_loss: 0.460, G_loss: 1.673
Epoch: [16/300]: D_loss: 0.487, G_loss: 1.669
Epoch: [17/300]: D_loss: 0.424, G_loss: 1.795
Epoch: [18/300]: D_loss: 0.428, G_loss: 1.881
Epoch: [19/300]: D_loss: 0.377, G_loss: 1.937
Epoch: [20/300]: D_loss: 0.401, G_loss: 1.966
Epoch: [21/300]: D_loss: 0.445, G_loss: 2.074
Epoch: [22/300]: D_loss: 0.396, G_loss: 2.062
Epoch: [23/300]: D_loss: 0.389, G_loss: 2.034
Epoch: [24/300]: D_loss: 0.414, G_loss: 2.075
Epoch: [25/300]: D_loss: 0.425, G_loss: 2.027
Epoch: [26/300]: D_loss: 0.391, G_loss: 1.994
Epoch: [27/300]: D_loss: 0.423, G_loss: 2.111
Epoch: [28/300]: D_loss: 0.416, G_loss: 2.003
Epoch: [29/300]: D_loss: 0.386, G_loss: 1.840
Epoch: [30/300]: D_loss: 0.467, G_loss: 1.810
Epoch: [31/300]: D_loss: 0.442, G_loss: 1.633
Epoch: [32/300]: D_loss: 0.443, G_loss: 1.596
Epoch: [33/300]: D_loss: 0.434, G_loss: 1.560
Epoch: [34/300]: D_loss: 0.449, G_loss: 1.587
Epoch: [35/300]: D_loss: 0.439, G_loss: 1.557
Epoch: [36/300]: D_loss: 0.431, G_loss: 1.554
Epoch: [37/300]: D_loss: 0.428, G_loss: 1.613
Epoch: [38/300]: D_loss: 0.439, G_loss: 1.682
Epoch: [39/300]: D_loss: 0.443, G_loss: 1.652
Epoch: [40/300]: D_loss: 0.424, G_loss: 1.648
Epoch: [41/300]: D_loss: 0.411, G_loss: 1.704
Epoch: [42/300]: D_loss: 0.414, G_loss: 1.660
Epoch: [43/300]: D_loss: 0.388, G_loss: 1.655
Epoch: [44/300]: D_loss: 0.444, G_loss: 1.799
Epoch: [45/300]: D_loss: 0.421, G_loss: 1.785
Epoch: [46/300]: D_loss: 0.393, G_loss: 1.799
Epoch: [47/300]: D_loss: 0.405, G_loss: 1.871
Epoch: [48/300]: D_loss: 0.631, G_loss: 2.149
Epoch: [49/300]: D_loss: 0.500, G_loss: 2.072
Epoch: [50/300]: D_loss: 0.368, G_loss: 1.778
Epoch: [51/300]: D_loss: 0.342, G_loss: 1.742
Epoch: [52/300]: D_loss: 0.361, G_loss: 1.813
Epoch: [53/300]: D_loss: 0.371, G_loss: 1.776
Epoch: [54/300]: D_loss: 0.358, G_loss: 1.856
Epoch: [55/300]: D_loss: 0.355, G_loss: 1.883
Epoch: [56/300]: D_loss: 0.367, G_loss: 1.951
Epoch: [57/300]: D_loss: 0.369, G_loss: 1.975
Epoch: [58/300]: D_loss: 0.398, G_loss: 1.967
Epoch: [59/300]: D_loss: 0.354, G_loss: 2.041
Epoch: [60/300]: D_loss: 0.379, G_loss: 2.055
Epoch: [61/300]: D_loss: 0.325, G_loss: 1.962
Epoch: [62/300]: D_loss: 0.625, G_loss: 2.460
Epoch: [63/300]: D_loss: 0.319, G_loss: 1.981
Epoch: [64/300]: D_loss: 0.334, G_loss: 1.965
Epoch: [65/300]: D_loss: 0.306, G_loss: 1.980
Epoch: [66/300]: D_loss: 0.343, G_loss: 2.000
Epoch: [67/300]: D_loss: 0.360, G_loss: 2.106
Epoch: [68/300]: D_loss: 0.307, G_loss: 2.094
Epoch: [69/300]: D_loss: 0.350, G_loss: 2.195
Epoch: [70/300]: D_loss: 0.316, G_loss: 2.107
Epoch: [71/300]: D_loss: 0.376, G_loss: 2.193
Epoch: [72/300]: D_loss: 0.518, G_loss: 2.452
Epoch: [73/300]: D_loss: 0.295, G_loss: 2.138
Epoch: [74/300]: D_loss: 0.281, G_loss: 2.125
Epoch: [75/300]: D_loss: 0.316, G_loss: 2.253
Epoch: [76/300]: D_loss: 0.319, G_loss: 2.275
Epoch: [77/300]: D_loss: 0.281, G_loss: 2.302
Epoch: [78/300]: D_loss: 0.366, G_loss: 2.401
Epoch: [79/300]: D_loss: 0.279, G_loss: 2.333
Epoch: [80/300]: D_loss: 0.340, G_loss: 2.428
Epoch: [81/300]: D_loss: 0.302, G_loss: 2.331
Epoch: [82/300]: D_loss: 0.289, G_loss: 2.362
Epoch: [83/300]: D_loss: 0.279, G_loss: 2.402
Epoch: [84/300]: D_loss: 0.378, G_loss: 2.497
Epoch: [85/300]: D_loss: 0.256, G_loss: 2.423
Epoch: [86/300]: D_loss: 0.423, G_loss: 2.575
Epoch: [87/300]: D_loss: 0.244, G_loss: 2.375
Epoch: [88/300]: D_loss: 0.299, G_loss: 2.450
Epoch: [89/300]: D_loss: 0.266, G_loss: 2.585
Epoch: [90/300]: D_loss: 0.241, G_loss: 2.529
Epoch: [91/300]: D_loss: 0.532, G_loss: 2.803
Epoch: [92/300]: D_loss: 0.268, G_loss: 2.494
Epoch: [93/300]: D_loss: 0.254, G_loss: 2.529
Epoch: [94/300]: D_loss: 0.260, G_loss: 2.561
Epoch: [95/300]: D_loss: 0.287, G_loss: 2.603
Epoch: [96/300]: D_loss: 0.280, G_loss: 2.699
Epoch: [97/300]: D_loss: 0.251, G_loss: 2.689
Epoch: [98/300]: D_loss: 0.269, G_loss: 2.616
Epoch: [99/300]: D_loss: 0.317, G_loss: 2.719
Epoch: [100/300]: D_loss: 0.241, G_loss: 2.725
Epoch: [101/300]: D_loss: 0.240, G_loss: 2.705
Epoch: [102/300]: D_loss: 0.415, G_loss: 2.979
Epoch: [103/300]: D_loss: 0.275, G_loss: 2.663
Epoch: [104/300]: D_loss: 0.212, G_loss: 2.714
Epoch: [105/300]: D_loss: 0.258, G_loss: 2.761
Epoch: [106/300]: D_loss: 0.235, G_loss: 2.864
Epoch: [107/300]: D_loss: 0.241, G_loss: 2.878
Epoch: [108/300]: D_loss: 0.251, G_loss: 2.849
Epoch: [109/300]: D_loss: 0.272, G_loss: 2.975
Epoch: [110/300]: D_loss: 0.632, G_loss: 3.080
Epoch: [111/300]: D_loss: 0.247, G_loss: 2.660
Epoch: [112/300]: D_loss: 0.273, G_loss: 2.752
Epoch: [113/300]: D_loss: 0.236, G_loss: 2.708
Epoch: [114/300]: D_loss: 0.198, G_loss: 2.844
Epoch: [115/300]: D_loss: 0.196, G_loss: 2.979
Epoch: [116/300]: D_loss: 0.219, G_loss: 2.869
Epoch: [117/300]: D_loss: 0.344, G_loss: 3.120
Epoch: [118/300]: D_loss: 0.231, G_loss: 2.877
Epoch: [119/300]: D_loss: 0.206, G_loss: 2.920
Epoch: [120/300]: D_loss: 0.283, G_loss: 3.014
Epoch: [121/300]: D_loss: 0.243, G_loss: 3.000
Epoch: [122/300]: D_loss: 0.216, G_loss: 2.998
Epoch: [123/300]: D_loss: 0.210, G_loss: 2.996
Epoch: [124/300]: D_loss: 0.247, G_loss: 3.008
Epoch: [125/300]: D_loss: 0.223, G_loss: 3.054
Epoch: [126/300]: D_loss: 0.433, G_loss: 3.214
Epoch: [127/300]: D_loss: 0.214, G_loss: 2.933
Epoch: [128/300]: D_loss: 0.202, G_loss: 3.036
Epoch: [129/300]: D_loss: 0.218, G_loss: 3.104
Epoch: [130/300]: D_loss: 0.242, G_loss: 3.100
Epoch: [131/300]: D_loss: 0.222, G_loss: 3.044
Epoch: [132/300]: D_loss: 0.206, G_loss: 3.176
Epoch: [133/300]: D_loss: 0.203, G_loss: 3.196
Epoch: [134/300]: D_loss: 0.509, G_loss: 3.196
Epoch: [135/300]: D_loss: 0.212, G_loss: 3.027
Epoch: [136/300]: D_loss: 0.220, G_loss: 3.135
Epoch: [137/300]: D_loss: 0.206, G_loss: 3.160
Epoch: [138/300]: D_loss: 0.217, G_loss: 3.129
Epoch: [139/300]: D_loss: 0.214, G_loss: 3.235
Epoch: [140/300]: D_loss: 0.249, G_loss: 3.295
Epoch: [141/300]: D_loss: 0.202, G_loss: 3.219
Epoch: [142/300]: D_loss: 0.174, G_loss: 3.282
Epoch: [143/300]: D_loss: 0.222, G_loss: 3.245
Epoch: [144/300]: D_loss: 0.368, G_loss: 3.445
Epoch: [145/300]: D_loss: 0.252, G_loss: 3.177
Epoch: [146/300]: D_loss: 0.236, G_loss: 3.241
Epoch: [147/300]: D_loss: 0.193, G_loss: 3.259
Epoch: [148/300]: D_loss: 0.205, G_loss: 3.209
Epoch: [149/300]: D_loss: 0.398, G_loss: 3.518
Epoch: [150/300]: D_loss: 0.355, G_loss: 2.940
Epoch: [151/300]: D_loss: 0.207, G_loss: 3.145
Epoch: [152/300]: D_loss: 0.176, G_loss: 3.273
Epoch: [153/300]: D_loss: 0.186, G_loss: 3.356
Epoch: [154/300]: D_loss: 0.187, G_loss: 3.397
Epoch: [155/300]: D_loss: 0.187, G_loss: 3.509
Epoch: [156/300]: D_loss: 0.180, G_loss: 3.426
Epoch: [157/300]: D_loss: 0.199, G_loss: 3.406
Epoch: [158/300]: D_loss: 0.216, G_loss: 3.369
Epoch: [159/300]: D_loss: 0.174, G_loss: 3.533
Epoch: [160/300]: D_loss: 0.239, G_loss: 3.474
Epoch: [161/300]: D_loss: 0.190, G_loss: 3.492
Epoch: [162/300]: D_loss: 0.218, G_loss: 3.462
Epoch: [163/300]: D_loss: 0.596, G_loss: 3.449
Epoch: [164/300]: D_loss: 0.201, G_loss: 3.284
Epoch: [165/300]: D_loss: 0.164, G_loss: 3.331
Epoch: [166/300]: D_loss: 0.164, G_loss: 3.401
Epoch: [167/300]: D_loss: 0.181, G_loss: 3.488
Epoch: [168/300]: D_loss: 0.153, G_loss: 3.466
Epoch: [169/300]: D_loss: 0.266, G_loss: 3.599
Epoch: [170/300]: D_loss: 0.236, G_loss: 3.516
Epoch: [171/300]: D_loss: 0.198, G_loss: 3.454
Epoch: [172/300]: D_loss: 0.179, G_loss: 3.512
Epoch: [173/300]: D_loss: 0.209, G_loss: 3.694
Epoch: [174/300]: D_loss: 0.200, G_loss: 3.631
Epoch: [175/300]: D_loss: 0.328, G_loss: 3.688
Epoch: [176/300]: D_loss: 0.215, G_loss: 3.448
Epoch: [177/300]: D_loss: 0.157, G_loss: 3.577
Epoch: [178/300]: D_loss: 0.174, G_loss: 3.643
Epoch: [179/300]: D_loss: 0.160, G_loss: 3.640
Epoch: [180/300]: D_loss: 0.468, G_loss: 3.804
Epoch: [181/300]: D_loss: 0.292, G_loss: 3.219
Epoch: [182/300]: D_loss: 0.170, G_loss: 3.529
Epoch: [183/300]: D_loss: 0.189, G_loss: 3.610
Epoch: [184/300]: D_loss: 0.164, G_loss: 3.635
Epoch: [185/300]: D_loss: 0.164, G_loss: 3.602
Epoch: [186/300]: D_loss: 0.143, G_loss: 3.636
Epoch: [187/300]: D_loss: 0.213, G_loss: 3.736
Epoch: [188/300]: D_loss: 0.158, G_loss: 3.714
Epoch: [189/300]: D_loss: 0.602, G_loss: 3.825
Epoch: [190/300]: D_loss: 0.241, G_loss: 3.278
Epoch: [191/300]: D_loss: 0.149, G_loss: 3.585
Epoch: [192/300]: D_loss: 0.155, G_loss: 3.773
Epoch: [193/300]: D_loss: 0.159, G_loss: 3.737
Epoch: [194/300]: D_loss: 0.159, G_loss: 3.697
Epoch: [195/300]: D_loss: 0.213, G_loss: 3.672
Epoch: [196/300]: D_loss: 0.187, G_loss: 3.765
Epoch: [197/300]: D_loss: 0.166, G_loss: 3.779
Epoch: [198/300]: D_loss: 0.207, G_loss: 3.795
Epoch: [199/300]: D_loss: 0.217, G_loss: 3.721
Epoch: [200/300]: D_loss: 0.165, G_loss: 3.774
Epoch: [201/300]: D_loss: 0.167, G_loss: 3.825
Epoch: [202/300]: D_loss: 0.210, G_loss: 3.816
Epoch: [203/300]: D_loss: 0.163, G_loss: 3.735
Epoch: [204/300]: D_loss: 0.138, G_loss: 3.939
Epoch: [205/300]: D_loss: 0.184, G_loss: 3.870
Epoch: [206/300]: D_loss: 0.948, G_loss: 3.548
Epoch: [207/300]: D_loss: 0.193, G_loss: 3.338
Epoch: [208/300]: D_loss: 0.156, G_loss: 3.499
Epoch: [209/300]: D_loss: 0.151, G_loss: 3.681
Epoch: [210/300]: D_loss: 0.187, G_loss: 3.718
Epoch: [211/300]: D_loss: 0.163, G_loss: 3.693
Epoch: [212/300]: D_loss: 0.139, G_loss: 3.891
Epoch: [213/300]: D_loss: 0.190, G_loss: 3.846
Epoch: [214/300]: D_loss: 0.147, G_loss: 3.884
Epoch: [215/300]: D_loss: 0.142, G_loss: 3.970
Epoch: [216/300]: D_loss: 0.147, G_loss: 3.910
Epoch: [217/300]: D_loss: 0.168, G_loss: 3.976
Epoch: [218/300]: D_loss: 0.303, G_loss: 3.909
Epoch: [219/300]: D_loss: 0.195, G_loss: 3.892
Epoch: [220/300]: D_loss: 0.174, G_loss: 3.972
Epoch: [221/300]: D_loss: 0.137, G_loss: 3.944
Epoch: [222/300]: D_loss: 0.130, G_loss: 4.064
Epoch: [223/300]: D_loss: 0.232, G_loss: 3.882
Epoch: [224/300]: D_loss: 1.054, G_loss: 3.227
Epoch: [225/300]: D_loss: 0.303, G_loss: 3.020
Epoch: [226/300]: D_loss: 0.180, G_loss: 3.376
Epoch: [227/300]: D_loss: 0.156, G_loss: 3.614
Epoch: [228/300]: D_loss: 0.162, G_loss: 3.662
Epoch: [229/300]: D_loss: 0.154, G_loss: 3.850
Epoch: [230/300]: D_loss: 0.160, G_loss: 3.855
Epoch: [231/300]: D_loss: 0.141, G_loss: 3.885
Epoch: [232/300]: D_loss: 0.127, G_loss: 3.995
Epoch: [233/300]: D_loss: 0.168, G_loss: 3.932
Epoch: [234/300]: D_loss: 0.199, G_loss: 4.070
Epoch: [235/300]: D_loss: 0.159, G_loss: 3.938
Epoch: [236/300]: D_loss: 0.164, G_loss: 3.964
Epoch: [237/300]: D_loss: 0.155, G_loss: 4.188
Epoch: [238/300]: D_loss: 0.130, G_loss: 4.045
Epoch: [239/300]: D_loss: 0.156, G_loss: 4.050
Epoch: [240/300]: D_loss: 0.147, G_loss: 4.113
Epoch: [241/300]: D_loss: 0.170, G_loss: 3.961
Epoch: [242/300]: D_loss: 0.334, G_loss: 4.144
Epoch: [243/300]: D_loss: 0.214, G_loss: 3.882
Epoch: [244/300]: D_loss: 0.166, G_loss: 3.929
Epoch: [245/300]: D_loss: 0.128, G_loss: 4.026
Epoch: [246/300]: D_loss: 0.152, G_loss: 4.079
Epoch: [247/300]: D_loss: 0.154, G_loss: 4.110
Epoch: [248/300]: D_loss: 0.166, G_loss: 4.103
Epoch: [249/300]: D_loss: 0.147, G_loss: 4.146
Epoch: [250/300]: D_loss: 0.138, G_loss: 4.187
Epoch: [251/300]: D_loss: 0.742, G_loss: 3.950
Epoch: [252/300]: D_loss: 0.348, G_loss: 3.056
Epoch: [253/300]: D_loss: 0.199, G_loss: 3.572
Epoch: [254/300]: D_loss: 0.165, G_loss: 3.863
Epoch: [255/300]: D_loss: 0.130, G_loss: 3.907
Epoch: [256/300]: D_loss: 0.146, G_loss: 4.080
Epoch: [257/300]: D_loss: 0.114, G_loss: 4.157
Epoch: [258/300]: D_loss: 0.159, G_loss: 4.159
Epoch: [259/300]: D_loss: 0.171, G_loss: 4.054
Epoch: [260/300]: D_loss: 0.144, G_loss: 4.094
Epoch: [261/300]: D_loss: 0.128, G_loss: 4.197
Epoch: [262/300]: D_loss: 0.134, G_loss: 4.270
Epoch: [263/300]: D_loss: 0.136, G_loss: 4.323
Epoch: [264/300]: D_loss: 0.323, G_loss: 3.848
Epoch: [265/300]: D_loss: 0.143, G_loss: 4.058
Epoch: [266/300]: D_loss: 0.154, G_loss: 4.234
Epoch: [267/300]: D_loss: 0.105, G_loss: 4.317
Epoch: [268/300]: D_loss: 0.203, G_loss: 4.201
Epoch: [269/300]: D_loss: 0.126, G_loss: 4.179
Epoch: [270/300]: D_loss: 0.114, G_loss: 4.469
Epoch: [271/300]: D_loss: 0.310, G_loss: 4.419
Epoch: [272/300]: D_loss: 0.290, G_loss: 3.825
Epoch: [273/300]: D_loss: 0.164, G_loss: 3.957
Epoch: [274/300]: D_loss: 0.131, G_loss: 4.092
Epoch: [275/300]: D_loss: 0.184, G_loss: 4.280
Epoch: [276/300]: D_loss: 0.159, G_loss: 4.202
Epoch: [277/300]: D_loss: 0.162, G_loss: 4.307
Epoch: [278/300]: D_loss: 0.134, G_loss: 4.288
Epoch: [279/300]: D_loss: 0.706, G_loss: 4.060
Epoch: [280/300]: D_loss: 0.349, G_loss: 3.264
Epoch: [281/300]: D_loss: 0.180, G_loss: 3.761
Epoch: [282/300]: D_loss: 0.153, G_loss: 3.928
Epoch: [283/300]: D_loss: 0.125, G_loss: 4.091
Epoch: [284/300]: D_loss: 0.118, G_loss: 4.230
Epoch: [285/300]: D_loss: 0.118, G_loss: 4.318
Epoch: [286/300]: D_loss: 0.121, G_loss: 4.301
Epoch: [287/300]: D_loss: 0.121, G_loss: 4.407
Epoch: [288/300]: D_loss: 0.134, G_loss: 4.409
Epoch: [289/300]: D_loss: 0.130, G_loss: 4.504
Epoch: [290/300]: D_loss: 0.099, G_loss: 4.481
Epoch: [291/300]: D_loss: 0.133, G_loss: 4.467
Epoch: [292/300]: D_loss: 1.226, G_loss: 3.049
Epoch: [293/300]: D_loss: 0.505, G_loss: 2.469
Epoch: [294/300]: D_loss: 0.301, G_loss: 3.053
Epoch: [295/300]: D_loss: 0.184, G_loss: 3.558
Epoch: [296/300]: D_loss: 0.185, G_loss: 3.656
Epoch: [297/300]: D_loss: 0.130, G_loss: 3.932
Epoch: [298/300]: D_loss: 0.137, G_loss: 4.029
Epoch: [299/300]: D_loss: 0.135, G_loss: 4.156
Epoch: [300/300]: D_loss: 0.130, G_loss: 4.1963、可视化¶
- 训练过程loss可视化
plt.figure(figsize=(10,5))
plt.title("Generator and Discriminator Loss During Training")
plt.plot(G_loss_plot,label="G")
plt.plot(D_loss_plot,label="D")
plt.xlabel("iterations")
plt.ylabel("Loss")
plt.legend()
plt.show()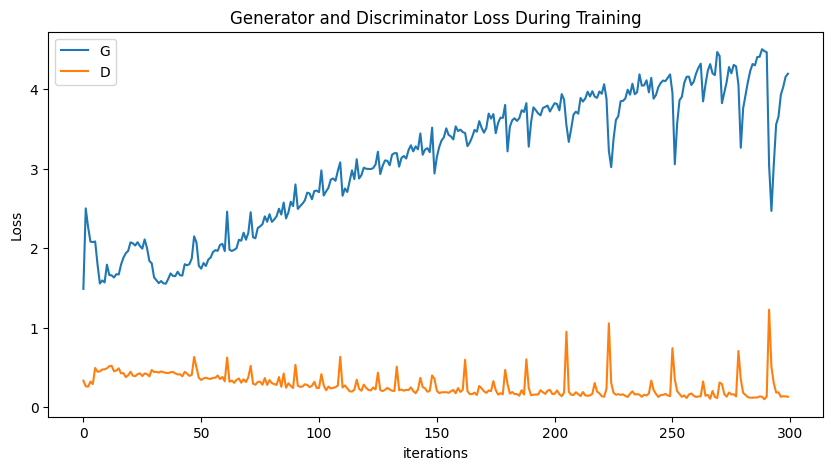
- 生成指定图像
predictions = predictions.permute(0,2,3,1)详解 这行代码是一个PyTorch(深度学习框架)中的操作,用于维度的重新排列: 假设predictions是一个PyTorch张量(tensor),它的维度为 (batch_size, height, width, channels),其中:
- batch_size:批量大小,表示张量中有多少个样本。
- height:高度,表示图像的高度(或特征图的高度)。
- width:宽度,表示图像的宽度(或特征图的宽度)。
- channels:通道数,表示图像或特征图的通道数,例如RGB图像的通道数为3。
predictions.permute(0, 2, 3, 1) permute是PyTorch中的一个函数,用于对张量的维度进行重新排列。在这个代码中,permute函数将张量的维度进行重新排列,以得到一个新的张量。具体地说,它将原始张量中的维度按照指定的顺序进行重新排列。 参数说明:
- 0, 2, 3, 1:这是一个指定新维度顺序的元组。在这里,它表示将原始维度中的第0维移到新张量的第0维,第2维移到新张量的第1维,第3维移到新张量的第2维,最后,第1维移到新张量的第3维。
所以,假设原始张量的形状是 (batch_size, height, width, channels),通过这行代码后,新张量的形状将变为 (batch_size, width, channels, height)。 这种维度重新排列在深度学习中非常常见,尤其是在卷积神经网络(Convolutional Neural Networks,CNNs)中,因为在某些情况下,不同的层需要不同的维度排列。permute函数就是为了帮助我们方便地处理这种情况,使得在不同层之间传递数据时更加高效和便捷。
# 导入所需的库
from numpy.random import randint, randn
from numpy import linspace
from matplotlib import pyplot, gridspec
# 导入生成器模型
generator.load_state_dict(torch.load('./training_weights/generator_epoch_300.pth'), strict=False)
generator.eval()
interpolated = randn(100) # 生成两个潜在空间的点
# 将数据转换为torch张量并将其移至GPU(假设device已正确声明为GPU)
interpolated = torch.tensor(interpolated).to(device).type(torch.float32)
label = 0 # 手势标签,可在0,1,2之间选择
labels = torch.ones(1) * label
labels = labels.to(device).unsqueeze(1).long()
# 使用生成器生成插值结果
predictions = generator((interpolated, labels))
predictions = predictions.permute(0,2,3,1).detach().cpu()#隐藏警告
import warnings
warnings.filterwarnings("ignore") #忽略警告信息
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
plt.rcParams['figure.dpi'] = 100 #分辨率
plt.figure(figsize=(8, 3))
pred = (predictions[0, :, :, :] + 1 ) * 127.5
pred = np.array(pred)
plt.imshow(pred.astype(np.uint8))
plt.show()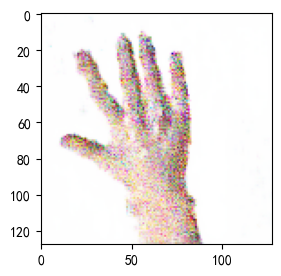




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律