面向对象编程课程(OOP)第三单元总结
第三单元课程概述
本单元的主人公是JML语言,全称为Java Modeling Language,即用于对Java程序进行规格化设计的一种表示语言。在前两个单元中,助教下发任务指导书,我们根据指导书的任务需求自行设计我们的架构,比如需要将需求抽象成哪些类,类之间的逻辑关系是什么样的,数据在每个类之间又是如何流通的等等。简单来说,我们在前两个单元中不仅做了架构师的工作,也做了编程人员的工作。
在第三单元中,我们的角色发生了变化,我们充当的是一个纯粹的编程人员的角色。助教不仅下发任务指导书,而且严格规定了需要的类,类里面需要存在的方法的功能,以及类与类之间的逻辑关系。我们在理解了任务指导书的前提之下,根据每一个方法的JML规格描述,填补每一个方法,以实现最终的功能。
本单元三次作业之间具有明显的继承关系。第一次作业完成Path和PathContainer两个类,第二次作业在第一次作业的基础上完成Graph类,而这个类是继承自PathContainer类的,第三次作业在第二次作业的基础上完成RailWaySystem类,这个类是继承自Graph类的。
一、JML是什么?JML怎么用?
JML是一种代码规格化设计的一种表示语言,有两种主要的用法。第一种就是借助JML开展规格化设计,这样交给代码人员的就不再是可能具有歧义的自然语言描述,而是逻辑严格的规格;第二种就是针对已有的代码来书写其规格,从而能够提高代码的可维护性,方便后续的维护人员对其进行维护。
JML表达式
需要注意的是,JML的表达式是对于Java表达式的一种扩展,Java的语法可以在JML中使用,还有一些Java中没有的表示方法也可以在JML中使用。
- \result:表示一个非void类型的方法执行所获得的结果
- \old(expr):表示一个表达式expr在相应方法执行前的取值
- \not_assigned(x,y,…):用来表示括号中的变量是否在方法执行过程中被赋值,如果没有被赋值,则返回true,反之则返回false
- \not_modified(x,y,…):用来表示括号中的变量是否在方法执行过程中被改变,如果没有被改变,则返回true,反之则返回false
- \typeof(expr):该表达式返回expr对应的准确类型
- \forall:全称量词修饰
- \exist:存在量词修饰
- \sum:返回给定范围内的表达式的和
- \produce:返回给定范围内的表达式的乘积
- \max:返回指定范围内的表达式的最大值
- \min:返回指定范围内的表达式的最小值
- \num_of:返回指定变量中满足相应条件的取值个数
方法规格
方法规格就是用来描述每个方法的具体行为的一段JML,可以分为以下几个部分:
- 前置条件。通过requires P来描述,即要求该方法的调用者确保P为真。
- 后置条件。通过ensures P来描述,即要求该方法的执行者确保方法执行完的结构一定满足谓词P的要求。
- 副作用范围限定。通过assginable或者modifiable来表示,描述方法对于对象的属性数据所造成的影响。
类型规格
类型规格即指针对Java程序中定义的数据类型所设计的限制规则。
- 不变式。通过invariant P来描述,即不管当前类处在什么状态,都必须满足谓词P的要求。
- 状态变化约束。通过constraint P来描述。即类的状态在每一次变化时,都必须满足谓词P的要求。
JML应用工具链
- 使用OpenJml中的-check选项来检查JML的规范性;
- 使用SMT Solver检查代码的等价性;
- 使用JML compiler(jmlc)来进行运行时断言检查;
- 使用jmlunit来自动化生成测试代码并进行单元测试;
- 使用Daikon来专门对类型规格中的不变式进行检查;
- ……还有许多利用JML的应用工具,等着我们在以后的学习中慢慢发掘!
二、部署JMLUnitNG自动生成测试用例
这一段的操作比较的繁琐,我在实践中也遇到了许多的难题,踩了许多的坑,下面我简单叙述一下大致的流程。
-
首先,从OpenJML的Github官方仓库中下载最新的release,解压下载的文件,将其中的三个jar包复制到一个新的文件夹中。
-
接着编写一个调用OpenJML的脚本,具体代码如下:
#!bin/bash java -jar /Users/mac/LearnOO/Files/openjml1/openjml.jar "$@"这个脚本的作用仅仅只是为了减少一些打字的工作量而已。
-
然后从JMLUnitNG的官网上下载jar包,类似OpenJML的安装过程。
-
由于前期遇到的种种困难,最终我只好选择拿MyPath类作为试验对象,同时由于\forall和\exist语句可能存在的问题,最终我只选择了size(),getNode()和isValid()三个方法来进行实验。实验代码如下:
package demo; import java.util.ArrayList; import java.util.HashSet; import java.util.Iterator; public class Demo { public ArrayList<Integer> nodes; public HashSet<Integer> nodeSet; private int hash = 0; public Demo() { } public Demo(int... nodeList) { this.nodes = new ArrayList<Integer>(); this.nodeSet = new HashSet<Integer>(); int sum = 0; int count = 0; for (int temp: nodeList) { this.nodes.add(temp); this.nodeSet.add(temp); count++; sum = (int)((sum + (long)(count * temp)) % (long)50021); } this.hash = sum; } //@ ensures \result == nodes.size(); public /*@pure@*/int size() { return this.nodes.size(); } /*@ requires index >= 0 && index < size(); @ assignable \nothing; @ ensures \result == nodes.get(index); @*/ public int getNode(int index) { return this.nodes.get(index); } //@ ensures \result == (nodes.size() >= 2); public boolean isValid() { return (this.nodes.size() >= 2); } } -
完成了需要测试的源代码之后,就是生成一系列测试文件了,终端中敲如下指令:
java -jar jmlunitng.jar demo/Demo.java -
此时我们可以看到demo文件夹下出现了许许多多的java文件,我们暂时不用管它们。
-
紧接着利用java和javac指令对生成的文件进行编译和运行,在终端中执行如下命令:
javac -cp jmlunitng.jar demo/*.java ./openjml -rac demo/Demo.java javac -cp jmlunitng.jar demo/*.java java -cp jmlunitng.jar demo.Demo_JML_Test可能大家会看到第一行和第三行是相同的,我也不清楚为什么要这么做,但是如果不这么做在我的机器上的确会出错。
-
最终得到的运行结果如下:
[TestNG] Running: Command line suite Failed: racEnabled() Passed: constructor Demo() Failed: constructor Demo(null) Passed: constructor Demo({}) Failed: <<demo.Demo@5f5a92bb>>.containsNode(-2147483648) Passed: <<demo.Demo@6fdb1f78>>.containsNode(-2147483648) Failed: <<demo.Demo@51016012>>.containsNode(0) Passed: <<demo.Demo@29444d75>>.containsNode(0) Failed: <<demo.Demo@1517365b>>.containsNode(2147483647) Passed: <<demo.Demo@44e81672>>.containsNode(2147483647) Failed: <<demo.Demo@4ca8195f>>.getDistinctNodeCount() Passed: <<demo.Demo@65e579dc>>.getDistinctNodeCount() Failed: <<demo.Demo@61baa894>>.getNode(-2147483648) Failed: <<demo.Demo@b065c63>>.getNode(-2147483648) Failed: <<demo.Demo@768debd>>.getNode(0) Failed: <<demo.Demo@7d4793a8>>.getNode(0) Failed: <<demo.Demo@449b2d27>>.getNode(2147483647) Failed: <<demo.Demo@5479e3f>>.getNode(2147483647) Failed: <<demo.Demo@27082746>>.isValid() Passed: <<demo.Demo@66133adc>>.isValid() Failed: <<demo.Demo@7bfcd12c>>.size() Passed: <<demo.Demo@42f30e0a>>.size() =============================================== Command line suite Total tests run: 22, Failures: 14, Skips: 0 ===============================================可以看到,在测试的时候主要生成的是边界用例,包括null,还有int的最大最小值等等。
三、作业架构分析
本单元的作业从架构上来说没有那么大的自由度了,因为具体的方法规格已经被设定好了,我们可以形象地理解为"戴着镣铐跳舞"。但同时,由于存在时间上的限制,所以我们需要对于数据的储存方式有比较好的把握,将某些复杂度较高的方法所需要完成的工作平摊至其他复杂度较低的方法中,并注重数据的缓存,避免许多无用功消耗大量的时间。
第一次作业
首先我们借助UML图看一下大致的架构。
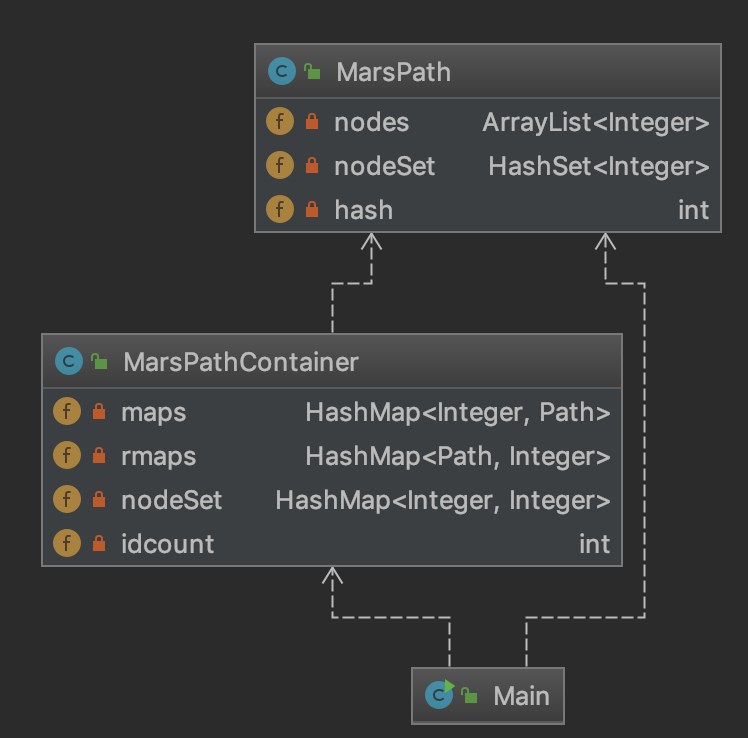
首先说一下MarsPath类。我是使用ArrayList来存储一条Path的节点序列的,因为其操作非常类似静态数组,同时其又是变长的,非常适合节点序列这种不变的序列。由于该类中有一个getDistinctNodeCount的方法,每一次调用该方法都对节点序列进行遍历显然不太好,既然阶段序列不变,那么只需要在创建该Path的时候计算一遍就行了,所以我设置了一个HashSet来存储不同的节点。因为HashSet是一种集合,所以其中肯定不会有相同的元素,正好与我的目标完全匹配。除此之外,我们对于两个Path相等的判定是节点序列完全相同即为相等,所以还需要改写其hashCode方法,在这里我也设置了一个int型变量来储存其hash值,这样不需要每次都进行计算。所有的初始化工作在构造函数中都已经完成了,所以一旦Path构建好,那么对其调用任何一个函数都只会是O(1)的复杂度了。构造函数如下。
public MarsPath(int... nodeList) {
this.nodes = new ArrayList<>();
this.nodeSet = new HashSet<>();
this.hash = 0;
int sum = 0;
int count = 0;
for (int temp: nodeList) {
this.nodes.add(temp);
this.nodeSet.add(temp);
count++;
sum = (int)((sum + (long)(count * temp)) % (long)50021);
}
this.hash = sum;
}
接下来说一下MarsPathContainer类。可以发现,该类的属性是一个三HashMap的构造,另外的那个int型属性idcount是用来给向容器中添加的每一个Path赋上id的。maps和rmaps都是用来记录Path和id之间的映射关系的,只不过二者的key-value对是相反的。这样设计是因为该类中既有由id得到Path的方法,又有由Path得到id的方法,所以为了避免遍历造成的时间开销,所以设立了两个HashMap。最后那个HashMap是用来存储不同节点个数的,但是为什么不直接用一个类似Path类的HashSet呢?因为在该类中,可能不同的Path中会有相同的节点,我们必须要记录该节点总共出现的次数,这样在删除某一条路径的时候,才能知道这些节点是否还有备份。所以在这个HashMap中,key是节点编号,而value则是该节点目前出现的次数。同样地,为了平摊时间复杂度,在添加或者删除路径时,我们把所有的属性都更新了,这样,对与该容器的内容查找的时间复杂度也是O(1)了。添加路径的示例如下:
public int addPath(Path path) throws Exception {
if (path == null || !path.isValid()) {
return 0;
} else {
if (!containsPath(path)) {
this.maps.put(++this.idcount, path);
this.rmaps.put(path, this.idcount);
addDistinctNode(path);
return this.idcount;
} else {
return getPathId(path);
}
}
}
第二次作业
UML图如下所示。
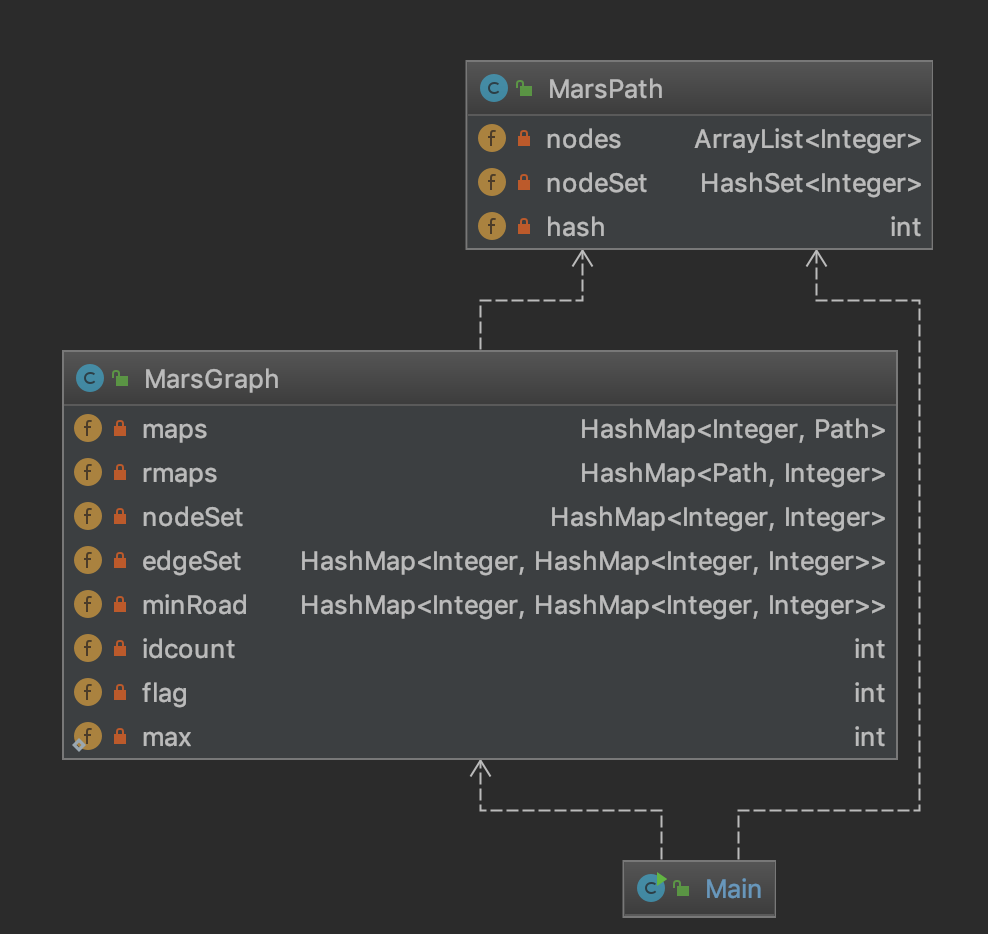
由于MarsPath类与第一次作业是完全相同的,所以我只介绍一下MarsGraph类。这个类继承了MarsPathContainer类,多添加的功能主要是判断两个节点的连通性和计算两个节点之间的最短路径长度。根据图论的知识,我们其实只需要一个距离矩阵就可以判断出是否连通以及最短路径长度,这个距离矩阵就是上图中的minRoad,这是一个二重嵌套HashMap结构,外层的key是节点i,内层的key是节点j,内层的value是这两个节点之间的最短路径,如果不连通,则值为max。flag是用来判断在上一次更新图结构之后是否有对于图的添加或删除操作,标示着图是否需要更新。
每当需要更新距离矩阵的时候,将原图删除,根据edgeSet来初始化距离矩阵,相邻的节点之间权值为1,自己到自己设为0,其他的都设为max值。然后使用BFS算法来计算所有点之间的最短路径,并存储在距离矩阵中。这里之所以使用BFS而不是Floyd算法是因为Floyd算法更加适用于点少边多的情况,但是我们一般生成的都是稀疏图,所以使用BFS的速率会明显加快很多。有关计算距离矩阵的代码如下;
for (int i: this.nodeSet.keySet()) {
this.minRoad.put(i, new HashMap<>());
for (int j: this.nodeSet.keySet()) {
if (i == j) {
this.minRoad.get(i).put(j, 0);
} else {
this.minRoad.get(i).put(j, max);
}
}
}
for (int k: this.nodeSet.keySet()) {
Queue<Integer> queue = new LinkedList<>();
queue.offer(k);
while (!queue.isEmpty()) {
int top = queue.poll();
if (this.edgeSet.get(top) == null) {
break;
}
HashMap<Integer, Integer> tmap = this.edgeSet.get(top);
for (int j: tmap.keySet()) {
if (this.minRoad.get(k).get(j) == max) {
this.minRoad.get(k).replace(j,
this.minRoad.get(k).get(top) + 1);
queue.offer(j);
}
}
}
}
第三次作业
UML图如下所示:
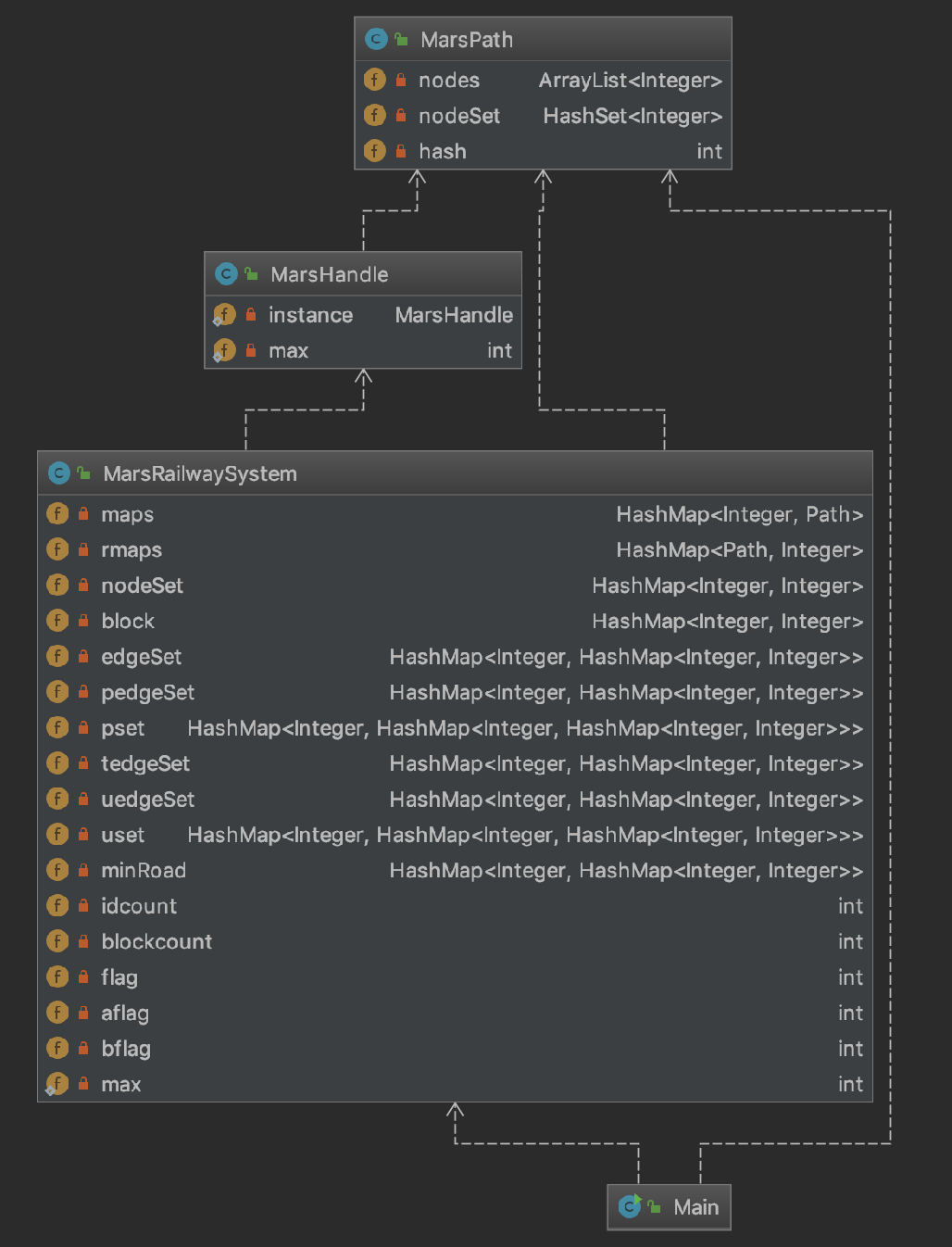
本次作业相对于上两次作业来说难度陡然提升,具体体现在需要分别计算最短换乘,最低票价和最小不满意度。 这其实是一个离散数学的问题,在最一开始,我的想法是拆点,即将不在一条路上的相同序号的节点当作两个节点进行计算。但是后来发现这样的计算开销太大太大了,虽然指导书说只有120个节点,但是这个是不同的节点数,如果路径之间节点的重叠度很高,那么图的规模就会非常的大。后来在讨论区看到了葛毅飞同学的思路(在此真诚感谢这位同学!!),将存在于同一个路径中的点先建成一个小的完全无向图,最终的图就是由这些小图拼接而成的,这样最短换乘,最低票价和最小不满意度的图结构都是相同的,唯一的区别在于边上的权值不同!所以首先在添加新路径到容器中时,就需要将小图建好,相关代码如下:
private void addDistinctMap(int id, Path path) {
ArrayList<Integer> t = ((MarsPath) path).getNodes();
HashMap<Integer, HashMap<Integer, Integer>> pmap = new HashMap<>();
HashMap<Integer, HashMap<Integer, Integer>> umap = new HashMap<>();
for (int i: ((MarsPath) path).getNodeSet()) {
pmap.put(i, new HashMap<>());
umap.put(i, new HashMap<>());
for (int j: ((MarsPath) path).getNodeSet()) {
if (i == j) {
pmap.get(i).put(j, 0);
umap.get(i).put(j, 0);
} else {
pmap.get(i).put(j, max);
umap.get(i).put(j, max);
}
}
}
for (int k = 0; k < t.size() - 1; k++) {
if (!t.get(k).equals(t.get(k + 1))) {
pmap.get(t.get(k)).replace(t.get(k + 1), 1);
pmap.get(t.get(k + 1)).replace(t.get(k), 1);
int un = getUnpleasantValue(t.get(k), t.get(k + 1));
umap.get(t.get(k)).replace(t.get(k + 1), un);
umap.get(t.get(k + 1)).replace(t.get(k), un);
}
}
for (int k: ((MarsPath) path).getNodeSet()) {
for (int i: ((MarsPath) path).getNodeSet()) {
for (int j: ((MarsPath) path).getNodeSet()) {
int pnow = pmap.get(i).get(j);
int ptrans = pmap.get(i).get(k) +
pmap.get(k).get(j);
if (pnow > ptrans) {
pmap.get(i).replace(j, ptrans);
}
int unow = umap.get(i).get(j);
int utrans = umap.get(i).get(k) +
umap.get(k).get(j);
if (unow > utrans) {
umap.get(i).replace(j, utrans);
}
}
}
}
for (int i: ((MarsPath) path).getNodeSet()) {
for (int j: ((MarsPath) path).getNodeSet()) {
if (i != j) {
pmap.get(i).replace(j, pmap.get(i).get(j) + 2);
umap.get(i).replace(j, umap.get(i).get(j) + 32);
}
}
}
this.pset.put(id, pmap);
this.uset.put(id, umap);
}
这里只有最低票价和最小不满意度的图生成,使用的是Floyd算法,最小换乘由于其规则的原因,不需要通过Floyd计算无向图各个边的权值,所以这里没有呈现。
每个Path的小图建好之后,在需要更新结果的时候,就只需要利用Floyd算法算出对应图的距离矩阵即可,该部分过程可以参考第二单元作业。唯一值得注意的地方是,在我最开始写的时候,仍旧使用的是HashMap模拟数组的功能,运算速度比较慢,后来我使用了静态数组,相同的算法运算速度快了很多。按照理论来说,HashMap的查找复杂度应该是O(1),应该与静态数组差不多快。但是我猜测,可能在寻找的时候,需要比对Hashcode的值,所以导致在大数据的时候速度放慢了许多。为了不影响我其他的架构,我是在即将计算的时候才开一个临时的静态数组,然后从HashMap中将数据复制进去,并且新建一个HashMap记录静态数组索引和节点编号的映射关系,算完之后,再将静态数组中的数据复制到HashMap中。这样一来,既可以比较清晰地记录距离矩阵,又可以保证比较快的计算速度。相关代码如下:
public void updateAll(HashMap<Integer, Integer> nodeSet,
HashMap<Integer, HashMap<Integer, Integer>>
pedgeSet,
HashMap<Integer, HashMap<Integer, Integer>>
tedgeSet,
HashMap<Integer, HashMap<Integer, Integer>>
uedgeSet) {
HashMap<Integer, Integer> nodetoindex = new HashMap<>();
HashMap<Integer, Integer> indextonode = new HashMap<>();
int[][] p = new int[130][130];
int[][] t = new int[130][130];
int[][] u = new int[130][130];
int index = 0;
for (int i: nodeSet.keySet()) {
nodetoindex.put(i, index);
indextonode.put(index, i);
index++;
}
for (int i = 0; i < nodeSet.size(); i++) {
int inode = indextonode.get(i);
for (int j = 0; j < nodeSet.size(); j++) {
if (i == j) {
p[i][j] = 0;
t[i][j] = 0;
u[i][j] = 0;
} else {
int jnode = indextonode.get(j);
p[i][j] = pedgeSet.get(inode).get(jnode);
t[i][j] = tedgeSet.get(inode).get(jnode);
u[i][j] = uedgeSet.get(inode).get(jnode);
}
}
}
for (int k = 0; k < nodeSet.size(); k++) {
for (int i = 0; i < nodeSet.size(); i++) {
for (int j = 0; j < nodeSet.size(); j++) {
int pnow = p[i][j];
int ptrans = p[i][k] + p[k][j];
if (pnow > ptrans) {
p[i][j] = p[i][k] + p[k][j];
}
int tnow = t[i][j];
int ttrans = t[i][k] + t[k][j];
if (tnow > ttrans) {
t[i][j] = t[i][k] + t[k][j];
}
int unow = u[i][j];
int utrans = u[i][k] + u[k][j];
if (unow > utrans) {
u[i][j] = u[i][k] + u[k][j];
}
}
}
}
for (int i = 0; i < nodeSet.size(); i++) {
int inode = indextonode.get(i);
for (int j = 0; j < nodeSet.size(); j++) {
int jnode = indextonode.get(j);
pedgeSet.get(inode).replace(jnode, p[i][j]);
tedgeSet.get(inode).replace(jnode, t[i][j]);
uedgeSet.get(inode).replace(jnode, u[i][j]);
}
}
}
迭代过程简介
这三次作业的任务有着非常明显的继承关系,每一次作业都只是在上一次作业的基础上增添一些功能而已。比较幸运的是,由于我在每次完成作业之前都会仔细考虑使用方法的扩展性,以及数据存储形式的兼容性,所以这三次作业我完完全全也是继承式的开发,也就是新的作业会完全沿用上一次的代码,只针对新的功能添加一些新的方法而已。也就是说,后两次作业我都没有进行任何重构。我觉得这主要是因为作业没有对空间进行比较严格的要求,所以可以使用许许多多不一样的容器来储存信息。三次作业都完成之后现在回头看,我觉得第三次作业的类中的属性有些过于繁杂了,其实可以将一些合并起来,或者使用更兼容的数据组织形式来完成。
不管怎么说,在这一单元的实践中,我着实体会到了一个好的架构和设计如何能够在扩展的时候做到游刃有余的。如果每次作业都需要重构,那将会是一种灾难。
四、关于Bug和Bug修复
比较幸运的是,在这一单元的作业中,我都没有被强测找到bug或者在互测环节被找到bug,但是我想谈一谈在编程过程中通过测试找到的一些bug。
第一次作业
- 没有重写Path类的hashCode方法导致容器中会存入两个节点序列完全相同的路径;
- 没有考虑到有些节点会在多个Path中出现,在remove的时候直接将其从HashSet中抹掉,导致不同节点个数错误;
- 在removeById函数中忘了更新几个HashMap;
第二次作业
- 初始化距离矩阵的时候没有把自己到自己边的权值设为0;
第三次作业
- 使用静态数组进行Floyd算法的时候没有更新节点编号和数组索引的映射关系;
- 在构建子图的时候最开始没有使用Floyd算法,而是直接通过节点的顺序来构图,这样一来就很难处理自成一个环的路径;
五、心得体会
于我来说,规格撰写是一种比较高效的开发手段,这种高效性既体现在个人独自完成的小项目中,也体现在多人合作完成的大项目中。如果是个人独自开发的项目,那么在开始编程之前设计好整个项目的架构,同时撰写每个方法的规格,这会使得我们在真正编程之前对于每一个细节都精心考虑,保证了逻辑的正确性。在之后的编写过程中,即使有些细节没有想到,也仅仅需要小范围地进行改动,而不需要整个设计重构。如果是多人合作的大项目,那么就更好理解了,每个人的思维方式都不尽相同,表达方式也因人而异,所以如果我们能够用一种标准的无二义性的语言进行相互的交流,那么显然效率会大大提升。同时,在撰写规格的同时,其实也是对于我们抽象能力的一种锻炼,如何将方法的行为用比较完备的形式表达出来,需要长时间的训练,同时也需要我们对于整个类的状态空间有一个比较好的把握。
其次,规格的存在使得我们对程序进行测试变得更加有条理性了。根据每个方法的规格,我们可以设计出与其临界状态相关的一些测试用例,来观察方法是否能够正确运行。进一步地,我们甚至可以通过利用离散数学的一些方法,对于规格是否完备自洽来进行验证,这样一来,程序的正确性就变成了一种可以证明的东西。只要我们的规格符合需求,并且程序完全符合规格,那么这个程序就是正确的。
本单元中我们主要练习的是如何根据规格来补充函数,欠缺的训练是如何自行设计架构然后撰写规格,我觉得后者更为重要。在今后的学习生活中,如果有可能的话,我希望自己能够多尝试撰写规格,然后根据规格进行开发,锻炼自己的抽象能力和编程能力。同时,这样的训练也有助于我们开发出扩展性好的程序。


