线性回归

1.1什么是线性回归

我们首先用弄清楚什么是线性，什么是非线性。

• 线性：两个变量之间的关系是一次函数关系的——图象是直线，叫做线性。

  注意：题目的线性是指广义的线性，也就是数据与数据之间的关系。

• 非线性：两个变量之间的关系不是一次函数关系的——图象不是直线，叫做非线性。

相信通过以上两个概念大家已经很清楚了，其次我们经常说的回归回归到底是什么意思呢。

• 回归：人们在测量事物的时候因为客观条件所限，求得的都是测量值，而不是事物真实的值，为了能够得到真实值，无限次的进行测量，最后通过这些测量数据计算回归到真实值，这就是回归的由来。

通俗的说就是用一个函数去逼近这个真实值，那又有人问了，线性回归不是用来做预测吗？是的，通过大量的数据我们是可以预测到真实值的。如果还是不明白，大家可以加一下我的微信：wei15693176 进行讨论。

1.2线性回归要解决什么问题

对大量的观测数据进行处理，从而得到比较符合事物内部规律的数学表达式。也就是说寻找到数据与数据之间的规律所在，从而就可以模拟出结果，也就是对结果进行预测。解决的就是通过已知的数据得到未知的结果。例如：对房价的预测、判断信用评价、电影票房预估等。

1.3线性回归的一般模型

大家看上面图片，图片上有很多个小点点，通过这些小点点我们很难预测当x值=某个值时，y的值是多少，我们无法得知，所以，数学家是很聪明的，是否能够找到一条直线来描述这些点的趋势或者分布呢？答案是肯定的。相信大家在学校的时候都学过这样的直线，只是当时不知道这个方程在现实中是可以用来预测很多事物的。

那么问题来了，什么是模型呢？先来看看下面这幅图。

假设数据就是x，结果是y，那中间的模型其实就是一个方程，这是一种片面的解释，但有助于我们去理解模型到底是个什么东西。以前在学校的时候总是不理解数学建模比赛到底在做些什么，现在理解了，是从题目给的数据中找到数据与数据之间的关系，建立数学方程模型，得到结果解决现实问题。其实是和机器学习中的模型是一样的意思。那么线性回归的一般模型是什么呢？

模型神秘的面纱已经被我们揭开了，就是以上这个公式，不要被公式吓到，只要知道模型长什么样就行了。假设i=0，表示的是一元一次方程，是穿过坐标系中原点的一条直线，以此类推。

1.4如何使用模型

我们知道x是已知条件，通过公式求出y。已知条件其实就是我们的数据，以预测房价的案例来说明：

上图给出的是某个地区房价的一些相关信息，有日期、房间数、建筑面积、房屋评分等特征，表里头的数据就是我们要的x1、x2、x3…….... 自然的表中的price列就是房屋的价格，也就是y。现在需要求的就是theta的值了，后续步骤都需要依赖计算机来训练求解。

1.5模型计算

当然，这些计算虽然复杂，但python库中有现成的函数直接调用就可以求解。我们为了理解内部的计算原理，就需要一步一步的来剖析计算过程。

为了容易理解模型，假设该模型是一元一次函数，我们把一组数据x和y带入模型中，会得到如下图所示线段。

是不是觉得这条直线拟合得不够好？显然最好的效果应该是这条直线穿过所有的点才是，需要对模型进行优化，这里我们要引入一个概念。

• 损失函数：是用来估量你模型的预测值 f(x)与真实值 YY 的不一致程度，损失函数越小，模型的效果就越好。

不要看公式很复杂，其实就是一句话，(预测值-真实值)的平法和的平均值，换句话说就是点到直线距离和最小。用一幅图来表示：

解释：一开始损失函数是比较大的，但随着直线的不断变化(模型不断训练)，损失函数会越来越小，从而达到极小值点，也就是我们要得到的最终模型。

这种方法我们统称为梯度下降法。随着模型的不断训练，损失函数的梯度越来越平，直至极小值点，点到直线的距离和最小，所以这条直线就会经过所有的点，这就是我们要求的模型(函数)。

以此类推，高维的线性回归模型也是一样的，利用梯度下降法优化模型，寻找极值点，这就是模型训练的过程。

 

1.6过拟合与欠拟合(underfitting and overfitting)

在机器学习模型训练当中，模型的泛化能力越强，就越能说明这个模型表现很好。什么是模型的泛化能力？

• 模型的泛化能力：机器学习模型学习到的概念在它处于学习的过程中时模型没有遇见过的样本时候的表现。

模型的泛化能力直接导致了模型会过拟合与欠拟合的情况。让我们来看看一下情况：

我们的目标是要实现点到直线的平方和最小，那通过以上图示显然可以看出中间那幅图的拟合程度很好，最左边的情况属于欠拟合，最右边的情况属于过拟合。

• 欠拟合：训练集的预测值，与训练集的真实值有不少的误差，称之为欠拟合。

• 过拟合：训练集的预测值，完全贴合训练集的真实值，称之为过拟合。

欠拟合已经很明白了，就是误差比较大，而过拟合呢是训练集上表现得很好，换一批数据进行预测结果就很不理想了，泛化泛化说的就是一个通用性。

解决方法

使用正则化项，也就是给梯度下降公式加上一个参数，即：

加入这个正则化项好处：

• 控制参数幅度，不让模型“无法无天”。

• 限制参数搜索空间

• 解决欠拟合与过拟合的问题。

看到这里是不是觉得很麻烦，我之前说过现在是解释线性回归模型的原理与优化，但是到了真正使用上这些方法是一句话的事，因为这些计算库别人已经准备好了，感谢开源吧！

 

代码实现

数据集

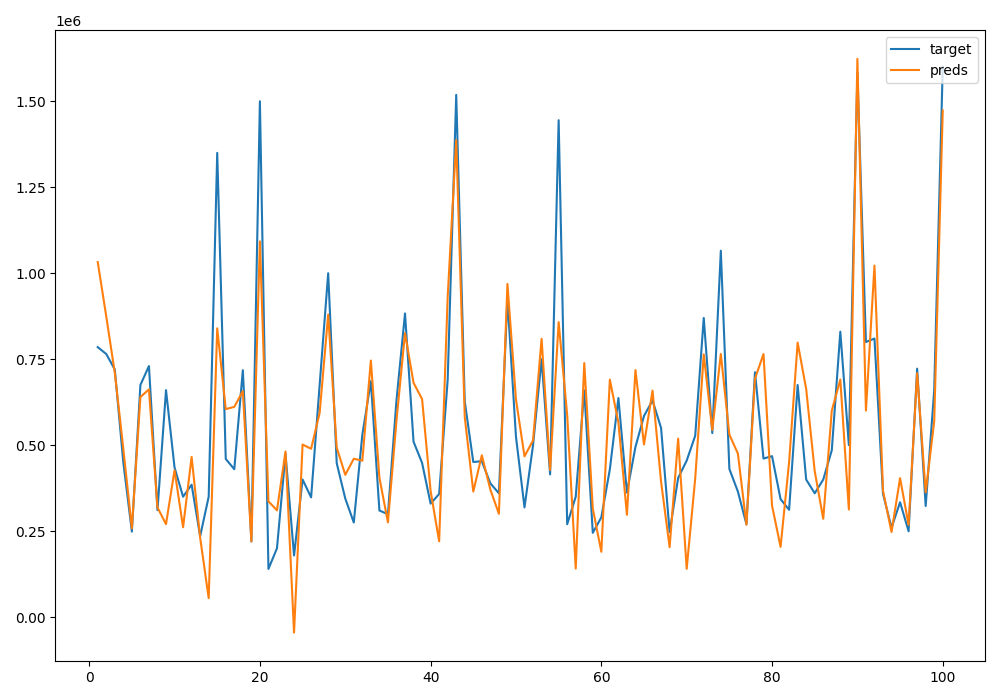
from __future__ import print_function

# 导入相关python库
import os
import numpy as np
import pandas as pd

#设定随机数种子
np.random.seed(36)

#使用matplotlib库画图
import matplotlib
import seaborn
import matplotlib.pyplot as plot

from sklearn import datasets


#读取数据
df=pd.read_csv('kc_train.csv')
df.columns=['销售日期','销售价格','卧室数','浴室数','房屋面积',
            '停车面积','楼层数','房屋评分','建筑面积','地下室面积',
            '建筑年份','修复年份','纬度','经度']
target=df['销售价格']
df.drop(labels=['销售价格'],inplace=True,axis=1)
housing=df
# housing = pd.read_csv('kc_train.csv')
# target=pd.read_csv('kc_train2.csv')  #销售价格
t=pd.read_csv('kc_test.csv')         #测试数据
t.columns=['销售日期','卧室数','浴室数','房屋面积',
            '停车面积','楼层数','房屋评分','建筑面积','地下室面积',
            '建筑年份','修复年份','纬度','经度']


#特征缩放
from sklearn.preprocessing import MinMaxScaler
minmax_scaler=MinMaxScaler()
minmax_scaler.fit(housing)
#进行内部拟合，内部参数会发生变化
scaler_housing=minmax_scaler.transform(housing)
scaler_housing=pd.DataFrame(scaler_housing,columns=housing.columns)

mm=MinMaxScaler()
mm.fit(t)
scaler_t=mm.transform(t)
scaler_t=pd.DataFrame(scaler_t,columns=t.columns)



#选择基于梯度下降的线性回归模型
from sklearn.linear_model import LinearRegression
LR_reg=LinearRegression()
#进行拟合
LR_reg.fit(scaler_housing,target)


#使用均方误差用于评价模型好坏
from sklearn.metrics import mean_squared_error
preds=LR_reg.predict(scaler_housing)   #输入数据进行预测得到结果
mse=mean_squared_error(preds,target)   #使用均方误差来评价模型好坏，可以输出mse进行查看评价值

#绘图进行比较
plot.figure(figsize=(10,7))       #画布大小
num=100
x=np.arange(1,num+1)              #取100个点进行比较
plot.plot(x,target[:num],label='target')      #目标取值
plot.plot(x,preds[:num],label='preds')        #预测取值
plot.legend(loc='upper right')  #线条显示位置
plot.show()


#输出测试数据
result=LR_reg.predict(scaler_t)
df_result=pd.DataFrame(result)
df_result.to_csv("result.csv")

结果如下：