如何将3D投影至2D平面--3D初探
前一段时间，组里分享一个关于3D投影至2D平面上的主题，一直没有时间细细的咀嚼一下。
每天的代码大部分都是在写业务逻辑，细想一下，自从毕业上班以来，一直没有去写过关于图形展示方面的东东，所以决定先入个门，以后要是有需求了也可以快速上手，也当补充一下高中的数学知识。
1，旋转
处理旋转需要用到一个旋转变换公式：
绕原点逆时针旋转 θ 度角的变换公式是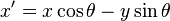 
与 
，用矩阵表示为：
由于是x,y,z的三维坐标系，所以根据上面的公式，可以得到如下的转换公式：
//向量旋转
function rotateX(x, y, z, a) {//绕X轴旋转
return {
x: x,
y: y * Math.cos(a) - z * Math.sin(a),
z: y * Math.sin(a) + z * Math.cos(a)
};
}
function rotateY(x, y, z, a) {//绕Y轴旋转
return {
x: x * Math.cos(a) + z * Math.sin(a),
y: y,
z: z * Math.cos(a) - x * Math.sin(a)
};
}
function rotateZ(x, y, z, a) {//绕Z轴旋转
return {
x: x * Math.cos(a) - y * Math.sin(a),
y: x * Math.sin(a) + y * Math.cos(a),
z: z
};
}2，球面坐标系转直角坐标系：
http://zh.wikipedia.org/wiki/%E5%9D%90%E6%A0%87%E7%B3%BB
球坐标系是用一个角度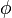 
表示位置和xy-面的相对关系。如P 点的球坐标为
。
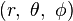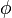是原点至P点之间的距离。 - 是线 OP 在 xy-面的投影线与正 x-轴之间的夹角。
为原点到点 P 的连线与正 z-轴之间的天顶角。
用球坐标 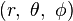来表示一个点的位置
而根据上面的介绍，可以写出下面的转换公式：
/*
* 球面坐标系转直角坐标系
* @param {Number} a 仰角的余角
* @param {Number} b 转角
* @param {Number} r 半径
*/
function spherical(a, b, r) {
return {
x: r * Math.sin(a) * Math.cos(b),
y: r * Math.sin(a) * Math.sin(b),
z: r * Math.cos(a)
};
}3，透视投影：
以上方的三维坐标系(x, y, z)为例，假设观察点设置在(1000, 0, 0)的A点上，而目标点B设置在(x < 0, y > 0, z >0)的区域内，并且设B点的坐标为Xb, Yb, Zb；设B点在YOZ平面上的投影的坐标是(0, Y’b. Z’b)，那么通过画图，可以得到一个公式：
1000 / (1000 - Xb) = Z’b / Zb (Xb < 0) == >> 这样就得到了Z’b（投影点的z坐标）和目标点B的原始Zb坐标之间和Xb坐标之间的关系；
同理：
1000 / ( - Xb) = Y’b / (Yb – Y’b) (Xb < 0)
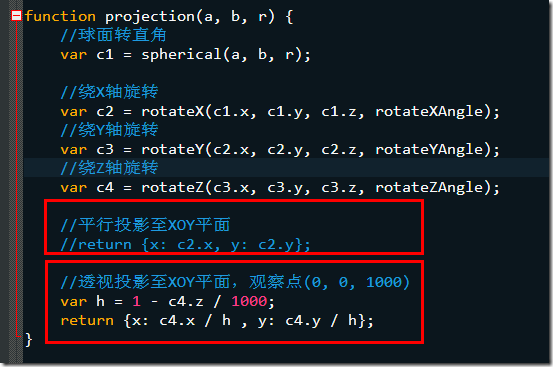
根据以上投影原理，可以列出以下代码片段：
主需要注意第二个红框，第一个红框是纯粹的平行投影（就像影子一样），第二个是透视投影，只是和上面说明的坐标系使用的不一样，但是原理是一样的。
----------
下面来看下整体代码吧：（不是原创，只是用来学习分享下）
不贴整体代码了，直接点击下方链接，太占地儿，直接新标签打开链接，查看源代码..
