回溯法解决最大团问题

• 问题描述

　　团是两两相邻顶点组成的集合。最大团是指一个图中所含顶点数最多的那个团。

 

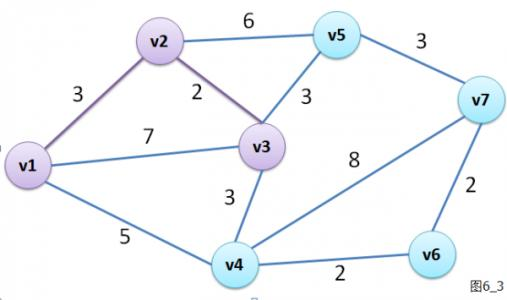
上图中顶点子集{v1,v2,v3,v4}就构成一个最大团。

独立集是两两不相邻顶点组成的集合。图G的团与图G补图/G的独立集之间存在一一对应的关系。U是G的最大团当且仅当U是/G的最大独立集。

• 算法设计

　　无向图的最大图和最大独立子集问题都可以用回溯法在O（n2ⁿ）时间内解决。图G的最大团和最大独立集问题都可以看成是图G顶点集V的子集选取问题。因此，可以用子集数表示问题的解空间。设当前要扩展的节点Z位于解空间的第i层。在进入左子树前，必须确认从顶点i到已选入的顶点集中每一个顶点都有边相连。在进入右子树之前，必须确认还有足够多的可选择顶点使得算法可能子右子树中找到更大团。

• 具体实现

# -*- coding: utf-8 -*-
"""
Created on Sun Oct 22 10:14:22 2017

@author: zhuhan
"""
import numpy as np

N = 5
a = np.random.randint(0, 2, (N, N))  #generate 0-1 random matrix as adjacent matrix
a = np.triu(a)
a += a.T - np.diag(a.diagonal())
for i in range(N):
    a[i][i] = 1
print(a)
cn = 0    #current number of vertex
bestn = 0   #current maximal number of vertex
x = np.zeros((N,))            #currrent solution
bestx =   np.zeros((N,))        #best solution
    
    
def backtrace( i ):
    global cn 
    global bestn
    if(i >= N):
        for j in range(N):
            bestx[j] = x[j]
        bestn = cn
        return 
    Ok = True     #检查顶点i与当前团的连接
    for j in range(i-1):
        if x[j] == 1 and (not a[i][j]):
            Ok = False
            break
    if Ok:                #进入左子树
        x[i] = 1 
        cn = cn + 1
        backtrace(i+1)
        cn = cn -1
    if cn + N-i-1 > bestn:
        x[i] = 0
        backtrace(i+1)
        

def main():
    backtrace(0)
    for i, j in enumerate(bestx):
        print(i,':',j)
        
if __name__ == '__main__':   
    main()  

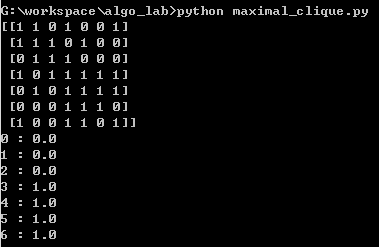
• 运行结果