课是英文的，bilibili上搜概率图就可以了，有些专业名词和句子我觉得自己翻译有失水准，所以就直接没翻译了。
概率图模型形式上是由图结构组成的。图的每个节点都关联了一个随机变量，而图的边则被用于编码这些随机变量之间的关系。
- 不确定性来源
Partial knowledge of state of the world
Noisy observation
Phenomena not covered by our model
Inherent stochasticity
- Probability Theory
Declarative representation with clear semantics
Powerful reasoning patterns
Established learning model
- 图模型的表示
直观简洁的数据结构
使用通用算法进行有效推理
稀疏的参数——feasible elicitation by hand and learning from data automatically
- 应用
自然语言处理（NLP）
图像分割
语音识别
- Graphical Models
Bayesian networks
1.Defination:
1）有向无环图（DAG），每个节点代表一个随机变量（random variable）
2）每个节点的条件概率分布（CPD）Xi~P(Xi | ParG(Xi) )
2.Factorization：
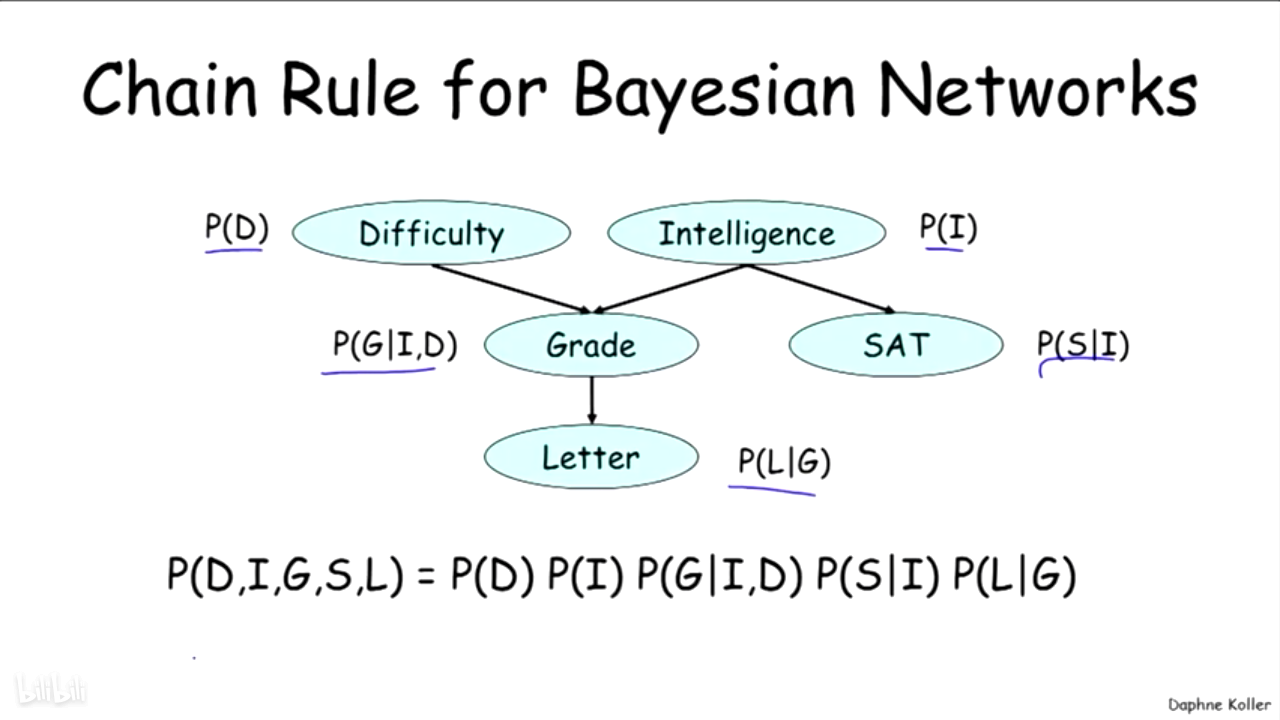
通过在Bayesian networks上应用链式法则得到BN是一个联合分布：P(X1,...,Xn) = ∏i P(Xi | ParG(Xi))
BN是一个正确的分布，因为满足下面两个条件：
1）P>=0： a product of CPDs and CPDs are non-negative
2）ΣP=1
3.Reasoning Patterns：
Causal Reasoning：从上到下利用链式法则计算，从原因推算结果
Evidential：从下到上利用贝叶斯公式计算，从结果推算导致的原因
Intercausal Reasoning：表明一个因素如何影响另一个因素，下图中说明Difficulty和Intelligence无关，但是当给定Grade的时候，这两个就有相关性了。
4.Flow of Probabilistic Influence：
类似于x->w<-y 这样的叫做v-structure，在第一张图里v-structure会阻止x对y产生影响。
由上面两个PPT的得出Active Trails的定义
5.Independence
Conditional Independence
Conditioning can lose independences
这个图也可以用来解释上面这句话。在图中X1和X2相互独立，如果给定y 的值，那么x1和x2之间不独立。如图中所示，给定y=1，P(x1=1|y)=2/3，但是P(x1=1|y) 的大小和x2的取值有关，如果X2取0，那么P(x1=1|y) =1，如果x2取1，P(x1=1|y)=1/2，此时x1和x2不独立。
6.d-sepatation
先给出了d-separated的定义：令X,Y,Z,是图G的三个节点集。在给定Z的情况下，假如任意节点Xi∈X，YI∈Y之间不存在Active Trails，那么X, Y是d-separated。
任何节点和自己的非子节点在给定该节点的父节点时都是d-separated。比如图中的Letter，给定父节点Grade，那么非子节点SAT、Intelligence、Difficulty和Coherence都和Letter是d-separated
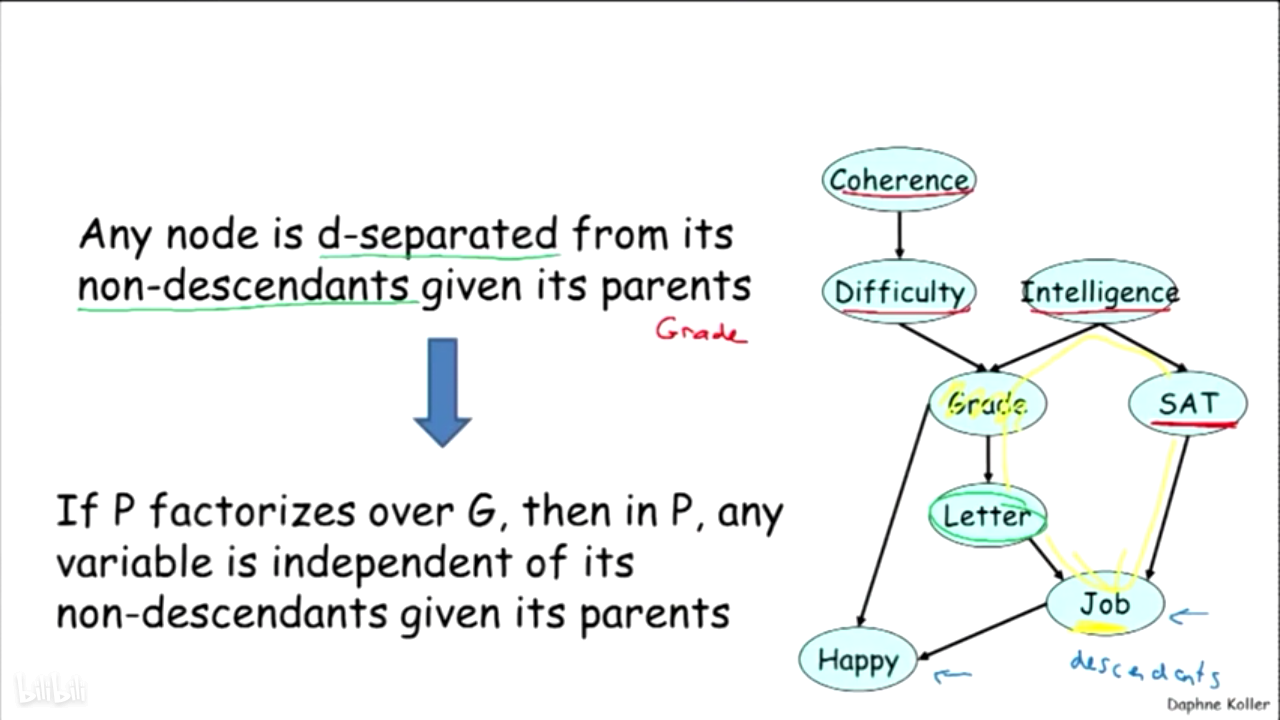
7.Indepence和Factorization的关系
Markov networks
