机器学习笔记
1. 梯度下降法
当\(n \geq 1\)时：
\(\theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)}) x^{(i)}_j\)
例如：
\(\theta_0 := \theta_0 - \alpha \frac{1}{m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)}) x^{(i)}_0\)
\(\theta_1 := \theta_1 - \alpha \frac{1}{m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)}) x^{(i)}_1\)
利用偏导数对参数进行迭代更新，参数\(\vec\theta\)沿着代价函数(cost function)的梯度下降，逐渐接近代价函数的极值。
2. Logistic Regression
-
定义：
\(h_\theta(x)=g(\theta^Tx)\),
\(g(z)=\cfrac1{1+e^{-z}}\)
-
逻辑回归中：
\(h_\theta (x) =\) (当输入为x时，\(y = 1\)的）概率
即\(h_\theta (x) = P( y=1|x;\theta)\)
且$ P( y=0|x;\theta)+P( y=1|x;\theta)=1$
-
decision boundary 决策边界
-
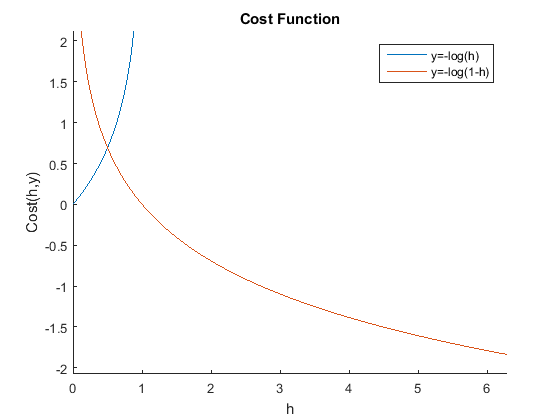
logistic regression cost function 逻辑回归代价函数
\(J(\theta)=\frac1m\sum_{i=1}^mCost(h\theta(x^{(i)},y^{(i)}))\)$Cost(h_\theta(x),y) =
\begin{cases}
-log(h_\theta(x)) & \text{if \(y=1\)} \
-log(1-h_\theta(x)) & \text{if \(y=0\)} \
\end{cases}$Note: y = 0 or 1 always
-
简化的代价函数和梯度下降法
\(Cost(h_\theta(x),y)=-ylog(h_\theta(x))\; - \; (1-y)log(1-h_\theta(x))\)
\(\begin{align} J(\theta) = & \frac1m\sum_{i=1}^mCost(h_\theta(x),y) \\ = & -\frac1m\left[\sum_{i=1}^my^{(i)}log(h_\theta(x^{(i)}))\; - \; (1-y^{(i)})log(1-h_\theta(x^{(i)}))\right] \end{align}\)
求得 \(\min_\theta J(\theta)\)
通过新的x预测：
输出\(h_\theta(x)=\cfrac1{1+e^{-\theta^Tx}}\)
(线性假设函数：\(h_\theta(x)=\theta^Tx\))
梯度下降法：Repeat {
\(\theta_j:=\theta_j-\alpha\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_j\)
所有\(\theta_j\)必须同步更新
}
-
高级优化算法
Given \(\theta\), we have code that can compute
- \(J(\theta)\)
- \(\frac\partial{\partial\theta_j}J(\theta)\) (for j = 0,1,...,n)
优化算法：
- Gradient descent
- Conjugate gradient
- BFGS
- L-BFGS
后三种算法的优点：
- 不需要选取学习率\(\alpha\)
- 往往比梯度下降法快
缺点：
- 更复杂
