[转]python起步之卡尔曼滤波
关于卡尔曼滤波的理论这里不打算讲了,就是那个5个基本的公式,这里直接给出公式:
公式1:X(k|k-1) = AX(k-1 | k-1) + BU(k) + W(k)
公式2:P(k|k-1) = AP(k-1|k-1)A' + Q(k)
公式3:X(k|k) = X(k|k-1) + Kg(k)[Z(k) - HX(k|k-1)
公式4:Kg(k) = P(k|k-1)H'/{HP(k|k-1)H' + R} //卡尔曼增益
公式5:P(k|k) = (1- Kg(k) H) P(k|k-1)
另外,Z(k) = HX(k) + V,Z是测量值,X是系统值,W是过程噪声,V是测量噪声,H是测量矩阵,A是转移矩阵,Q是W的协方差,R是V的协方差,X(k|k-1)是估计值;X(k|k)是X(k|k-1)的最优估计值,即滤波估计值;P(k|k-1)是估计值误差方差矩阵,P(k|k)是滤波误差方差矩阵。
下面给出Python版本的卡尔曼滤波小程序,这里设置A=1,H=1,BU=0,W=0:
# -*- coding=utf-8 -*-
# Kalman filter example demo in Python
# A Python implementation of the example given in pages 11-15 of "An
# Introduction to the Kalman Filter" by Greg Welch and Gary Bishop,
# University of North Carolina at Chapel Hill, Department of Computer
# Science, TR 95-041,
# http://www.cs.unc.edu/~welch/kalman/kalmanIntro.html
# by Andrew D. Straw
#coding:utf-8
import numpy
import pylab
#这里是假设A=1,H=1的情况
# intial parameters
n_iter = 50
sz = (n_iter,) # size of array
x = -0.37727 # truth value (typo in example at top of p. 13 calls this z)
z = numpy.random.normal(x,0.1,size=sz) # observations (normal about x, sigma=0.1)
Q = 1e-5 # process variance
# allocate space for arrays
xhat=numpy.zeros(sz) # a posteri estimate of x
P=numpy.zeros(sz) # a posteri error estimate
xhatminus=numpy.zeros(sz) # a priori estimate of x
Pminus=numpy.zeros(sz) # a priori error estimate
K=numpy.zeros(sz) # gain or blending factor
R = 0.1**2 # estimate of measurement variance, change to see effect
# intial guesses
xhat[0] = 0.0
P[0] = 1.0
for k in range(1,n_iter):
# time update
xhatminus[k] = xhat[k-1] #X(k|k-1) = AX(k-1|k-1) + BU(k) + W(k),A=1,BU(k) = 0
Pminus[k] = P[k-1]+Q #P(k|k-1) = AP(k-1|k-1)A' + Q(k) ,A=1
# measurement update
K[k] = Pminus[k]/( Pminus[k]+R ) #Kg(k)=P(k|k-1)H'/[HP(k|k-1)H' + R],H=1
xhat[k] = xhatminus[k]+K[k]*(z[k]-xhatminus[k]) #X(k|k) = X(k|k-1) + Kg(k)[Z(k) - HX(k|k-1)], H=1
P[k] = (1-K[k])*Pminus[k] #P(k|k) = (1 - Kg(k)H)P(k|k-1), H=1
pylab.figure()
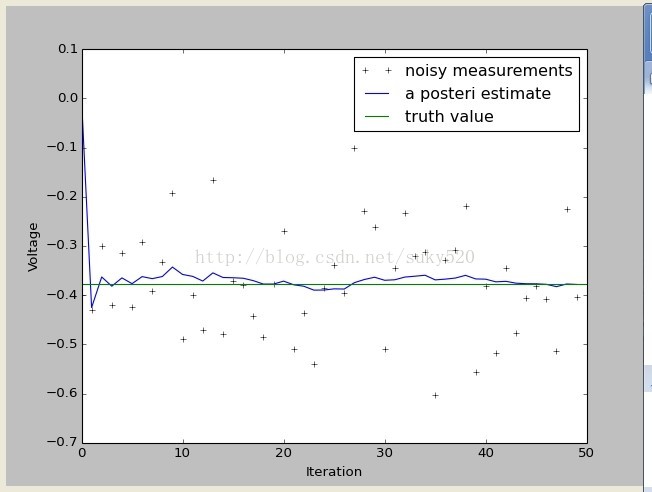
pylab.plot(z,'k+',label='noisy measurements') #测量值
pylab.plot(xhat,'b-',label='a posteri estimate') #过滤后的值
pylab.axhline(x,color='g',label='truth value') #系统值
pylab.legend()
pylab.xlabel('Iteration')
pylab.ylabel('Voltage')
pylab.figure()
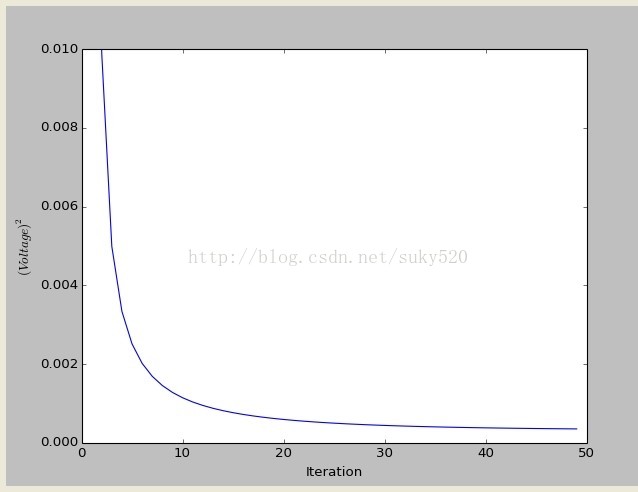
valid_iter = range(1,n_iter) # Pminus not valid at step 0
pylab.plot(valid_iter,Pminus[valid_iter],label='a priori error estimate')
pylab.xlabel('Iteration')
pylab.ylabel('$(Voltage)^2$')
pylab.setp(pylab.gca(),'ylim',[0,.01])
pylab.show()
结果:
作者:catmelo
本文版权归作者所有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文链接,否则保留追究法律责任的权利。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号