二叉排序树

1、先看一个需求

给你一个数列 (7, 3, 10, 12, 5, 1, 9)，要求能够高效的完成对数据的查询和添加。

1.1、解决方案分析

使用数组
数组未排序， 优点：直接在数组尾添加，速度快。 缺点：查找速度慢. [示意图]
数组排序，优点：可以使用二分查找，查找速度快，缺点：为了保证数组有序，在添加新数据时，找到插入位置后，后面的数据需整体移动，速度慢。[示意图]

使用链式存储-链表
不管链表是否有序，查找速度都慢，添加数据速度比数组快，不需要数据整体移动。[示意图]

使用二叉排序树

2、二叉排序树介绍

二叉排序树：BST: (Binary Sort(Search) Tree), 对于二叉排序树的任何一个非叶子节点，要求左子节点的值比当前节点的值小，右子节点的值比当前节点的值大。
特别说明：如果有相同的值，可以将该节点放在左子节点或右子节点

比如针对前面的数据 (7, 3, 10, 12, 5, 1, 9) ，对应的二叉排序树为：

3、二叉排序树创建和遍历

一个数组创建成对应的二叉排序树，并使用中序遍历二叉排序树，比如: 数组为 Array(7, 3, 10, 12, 5, 1, 9) ， 创建成对应的二叉排序树为 :

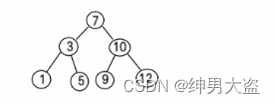
3.1、代码实现

package com.qf.treesort;

import java.util.Map;

public class BinarySortTreeDemo {
    public static void main(String[] args) {
        BinarySortTree binarySortTree=new BinarySortTree();
        binarySortTree.add(new Node(10));
        binarySortTree.add(new Node(12));
        binarySortTree.add(new Node(8));
        binarySortTree.add(new Node(9));
        binarySortTree.add(new Node(7));
        binarySortTree.add(new Node(6));
        binarySortTree.midOrder();
    }
}

class BinarySortTree{
    public Node root;

    public void add(Node node){
        if (root==null){
            root=node;
        }else{
            root.add(node);
        }
    }

    public void midOrder(){
        if (root==null){
            System.out.println("树为空~~~");
        }else{
            root.midOrder();
        }
    }
}
class Node{
    public int value;
    public Node left;
    public Node right;

    public Node(int value){
        this.value=value;
    }

    @Override
    public String toString() {
        return "Node{" +
                "value=" + value +
                '}';
    }

    public void add(Node node){
        if (this==null){
            return;
        }
        if (this.value>node.value){
            if (this.left==null){
                this.left=node;
            }else{
                this.left.add(node);
            }
        }else{
            if (this.right==null){
                this.right=node;
            }else{
                this.right.add(node);
            }
        }
    }

    public void midOrder(){
        if (this.left!=null){
            this.left.midOrder();
        }

        System.out.println(this);

        if (this.right!=null){
            this.right.midOrder();
        }
    }
}