【零基础】看懂神经网络中的反向传播

一、序言

　　反向传播在神经网络中用于优化权重w和阈值b，是神经网络优化的核心算法。经过数日的学习终于看明白了一点反向传播的原理，这里作文记录心得。

　　本文先介绍一下基本的数学计算方法，然后根据“损失计算公式”推导出优化参数的反向传播方法。

二、基本数学原理

　　神经网络中优化参数w、b的方法称为反向传播，反向传播的具体实施方法称为“梯度下降”，梯度下降涉及两个基本的数学知识：求导、链式法则。

　　1）求导

　　假设有以下式：

　　

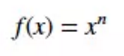
　　上式对x求导：

　　

 

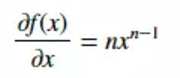
 　　实例：

　　

 

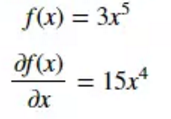
 　　2）链式法则

　　

 

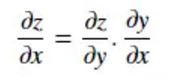
 　　链式法则的意义在于将z对x的求导转化为z对y的求导和y对x的求导，示例如下：

　　

 

 　　

 

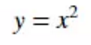
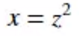
　　求y对z的导数

 　　

 

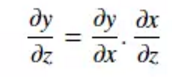
 　　已知：

　　

 

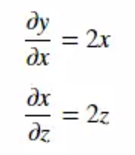
　　所以：

　　

 

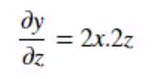
　　3）求导的数学意义

　　

 

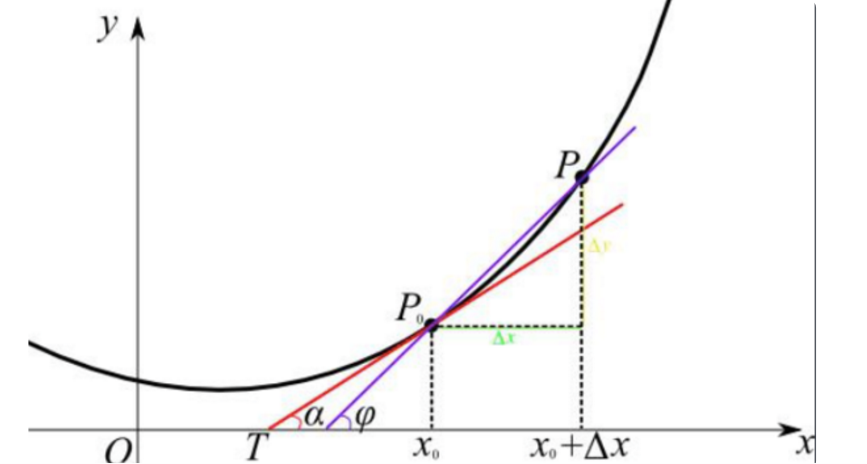
　　如上图所示，y对于x的导数本质上是求得x0处的斜率，若我们将x0增大一点点Δx，就可求得y轴上增大了多少Δy：

　　Δy = Δx*（x0处的斜率）

　　若我们想让y值趋向于最小，可以用y减去Δy：

　　y = y0-Δy = y0-Δx*（x0处的斜率）

　　其中y0、Δx、x0处的斜率都是已知的，我们就可以逐步趋近最小的y值。需要注意的是Δy只是一个近似的y轴增大量，不是实际的，但我们可以通过这个方法不断“逼近”y 的最小值。

三、损失计算

　　考虑一个简单的传播函数：

　　y = wx + b

　　其中w是权重、b是阈值、x是输入、y是预测输出，我们可以用预测输出减去实际输出得到损失（预测与实际之间的差异）：

 

 　　实际操作中我们会取误差的平方，因为平方差使得导出回归线更容易。只是为了降低运算难度，使用误差或误差的平方来衡量损失本质上没有区别。

　

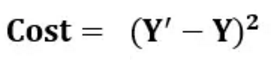
　　实际使用时，Y其实是个常数（label值），引入传播函数（Y撇）=wx+b

　　Cost = (wx+b - Y)^2

 

四、梯度下降

　　看上面的损失计算公式，会发现其实它是个抛物线，可以简化为y = x^2：

 

　　让预测结果趋向于实际结果，本质上就是要找到一个最小的cost，也就是使上图中y趋向于0。有一点需要注意的是，在下式中：

　　Cost = (wx+b - Y)^2

　　我们期望的是找到一个最佳的w和b来求得最小的Cost，其中x和Y其实都是已知的。所以我们是对w和b求导求得Δw和Δb。为便于计算，我们可以做以下变化：

　　Cost = (Error)^2

　　Error = wx+b-Y

　　

 

 　　

 

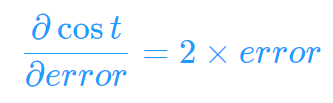
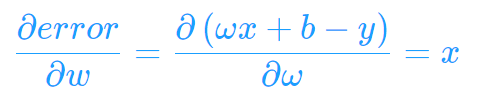
 　　根据链式法则，我们就可以得到：

　　

 

　　所以Δw = 2*error*x

　　类似地可以推导出Δb=2*error

　　在实际使用时，error值、x值都是已知的所以我们可以求得Δw和Δb

 

 　　上述反向传播的实现代码中，img即是x，Y-label即是error，除以m是因为实际操作时是一次对m个图片进行处理，这里求dw、db时需要取平均值所以除以m。其次实际代码中我们把Δw = 2*error*x的常数2忽略了，对实际操作没有影响。

五、总结

　　最后在优化参数时，我们会用Δw和Δb乘以一个非常小的浮点数如0.001称为步幅（learning rate），再用w-Δw、b-Δb。所以本质上来说Δw和Δb只是指明了梯度下降的方向，比如在下面的函数图形中，在x轴左侧应当增大x值，在x轴右侧则应该减小x值，我们通过斜率就可以知道具体应该减少还是增大了。

请关注公众号“零基础爱学习”一起AI学习。