【零基础】深层神经网络解析
回顾:
一、序言
前面我们已经完成了单神经元、浅层神经网络(2层)的解析,其中有很多没有讲透的地方我们就暂时不要理会了,比如反向传播的原理我也没看明白呢。这里我们继续下一步,解析深层的神经网络(N层),也就是真的要“深度学习”了。
注:本文内容主要是对“床长”的系列教程进行总结,强烈推荐“床长”的人工智能系列教程(https://www.captainbed.net/)
二、深层神经网络的构成
我们再回顾一下前面做的工作,一个典型的神经元构成如下:
1)传播函数,由输入x、偏置w、阈值b计算出a
2)激活函数,将a映射到0~1之间的结果y,可理解为(是、否)的概率
3)反向传播函数,通过y、label计算出dw、db(用以更新w和b)
4)损失函数,计算y与label间的误差
在浅层神经网络中,其实主要也是实现了这四个函数,区别只是在输入与输出间多了一层计算。以反向传播函数为例:
单神经元反向传播函数:

具有两层的浅层神经网络:

可以看到整体形式上并没有太大差别,而对于神经元层数更多的深层神经网络,其实大体上也是一样,只是我们需要用一个“循环”来处理一下可自定义的网络层数。
对于深层神经网络,我们在构建模型时不限制其网络层数、神经元个数,只是在使用时根据需要写上网络结构即可。下面依然是直接上代码,文末附完整代码文件下载。
这里我们依旧是处理前面“浅层神经网络”的问题“从图片中识别出偶数和奇数“。
三、随机初始化参数
#初始化所有层的w和b
def initialize_parameters(layer_dims):
np.random.seed(1)
wGroup = {}
bGroup = {}
layer = len(layer_dims)#神经网络总共有几层
#逐层初始化w、b
for i in range(1,layer): #i的值是1 2 3 到layer-1 的标号是从0开始的,其中layer_dims[0]是输入层
wGroup[str(i)] = np.random.randn(layer_dims[i],layer_dims[i-1])/np.sqrt(layer_dims[i-1])
bGroup[str(i)] = np.zeros((layer_dims[i],1))
return wGroup,bGroup
layer_dims包含了每层神经元个数,如[10,5,4,1]表示是一个三层的网络,第一层5个神经元、第二层4个神经元、第三层1个神经元。注意输入层是不算一层的,但是输入层的个数又直接影响了第一层w的初始化。
返回值wGroup,bGroup包含了每一层初始化后的w和b
四、传播函数
#传播函数
def forward(img, wGroup, bGroup):
#神经网络的实际层数与参数的层数一致
layer = len(wGroup)
#除第一层神经网络的输入是img,其他层的输入都是上一层的输出
#除最后一层的激活函数是sigmoid,其他层的激活函数都是relu
caches = []
Y = []
#前L-1层使用relu作为激活函数,最后一层使用sigmoid做激活函数
for i in range(1,layer+1):
if i == 1:
IN = img
else:
IN = Y#IN 就是Y_prev
w = wGroup[str(i)]
b = bGroup[str(i)]
A = np.dot(w, IN) + b
#将变量数据保存起来便于后面反向计算
caches.append((IN,w,b,A))
#下一层的输入使用激活函数转化一下
if i != layer:
Y = relu(A)
else:
Y = sigmoid(A)
return Y, caches
这里,除第一层的输入是img之外,后面都是用激活函数转化后的Y值作为输入。其中最后一层使用sigmoid作为激活函数,其他层使用relu函数(又换了个激活函数)。
这里的IN其实就是上一层的Y,caches里存储了IN:上一层的Y(其实就是本层的输入,第一层是img)、w:本层的权重、b:本层的偏置、A:激活前的乘积。将这些数据保存起来后面计算反向传播时用。最后还返回了最终的Y,其实就是神经网络最后的输出值。
五、反向传播函数
#反向传播
def backward(YLast,label,caches):
layer = len(caches)
label = label.reshape(YLast.shape)
dWGroup = {}
dbGroup = {}
Y = YLast
(Y_prev, W, b, A) = caches[-1]#取最后一个值
m = Y_prev.shape[1]
#直接计算最后一层dY
dY = - (np.divide(label, Y) - np.divide(1 - label, 1 - Y+0.000001))#这里加上一个0.000001是为了防止1-Y=0
#最后一层dA dW db
dA = sigmoid_backward(dY, A)
dW = np.dot(dA, Y_prev.T) / m
db = np.sum(dA, axis=1, keepdims=True) / m
dWGroup[str(layer)] = dW
dbGroup[str(layer)] = db
#上一层的dY
dY_prev = np.dot(W.T, dA)
for c in reversed(range(1,layer)):#若layer=4则C =3 2 1
dY = dY_prev
(Y_prev, W, b, A) = caches[c-1]#c-1 = 2 1 0,这里不好理解的是c是从1开始的,而caches是从0开始的
m = Y_prev.shape[1]
dA = relu_backward(dY, A)
dW = np.dot(dA, Y_prev.T) / m
db = np.sum(dA, axis=1, keepdims=True) / m
#上一层的dA
dY_prev = np.dot(W.T, dA)
dWGroup[str(c)] = dW
dbGroup[str(c)] = db
return dWGroup,dbGroup
这里的反向传播其实本质上跟浅层神经网络差不多,只是我们将最后一层的反向传播单独拿出来计算(因为激活函数不同),而且又涉及到历史参数获取(之前直接作为参数传)只是看起来复杂。你可以自己尝试结合前面浅层网络做一个指定层数(比如3层)的代码编写,只有动起手来才好理解。下面是我自己写的一段帮助理解的伪代码。另外需要注意的是,这里计算dA时分别针对relu和sigmoid函数是不一样的,所以分别有relu_backward和sigmoid_backward函数。

六、梯度下降(更新w、b)
#更新w、b参数
def update(wGroup, bGroup, dWGroup, dbGroup, learning_rate):
L = len(wGroup)
for i in range(1,L+1): #1-3
wGroup[str(i)] = wGroup[str(i)] - learning_rate * dWGroup[str(i)]
bGroup[str(i)] = bGroup[str(i)] - learning_rate * dbGroup[str(i)]
return wGroup,bGroup
七、损失函数
#损失函数
def costCAL(Y, label):
m = label.shape[1]
cost = np.multiply(label,np.log(Y))+np.multiply(1-label, np.log(1-Y+0.000001))#这里加个很小的数是为了防止1-Y=0的情况
cost = -np.sum(cost)/m
cost = np.squeeze(cost)
return cost
八、预测函数
#预测函数
def predict(img,wGroup,bGroup):
m = img.shape[1]
L = len(wGroup)
p = np.zeros((1,m))
#向前传播做预测
probas,caches = forward(img, wGroup, bGroup)
# 将预测结果转化成0和1的形式,即大于0.5的就是1,否则就是0
for i in range(0, probas.shape[1]):
if probas[0,i] > 0.5:
p[0,i] = 1
else:
p[0,i] = 0
return p
九、训练模型并预测
#组成训练model
def model(img, label, layers_dims, learning_rate=0.0075, num_iterations=3000, print_cost=False):
np.random.seed(1)
costs = []
wGroup,bGroup = initialize_parameters(layers_dims)
#训练若干次数
for i in range(0, num_iterations):
#向前传播
Y,caches = forward(img, wGroup, bGroup)
# 计算成本
cost = costCAL(Y, label)
# 进行反向传播
dWGroup,dbGroup = backward(Y,label,caches)
# 更新参数,好用这些参数进行下一轮的前向传播
wGroup,bGroup = update(wGroup, bGroup, dWGroup, dbGroup, learning_rate)
# 打印出成本
if i % 100 == 0:
if print_cost and i > 0:
print ("训练%i次后成本是: %f" % (i, cost))
return wGroup,bGroup
#训练并预测
layers_dims = [784, 20, 7, 5, 1]
wGroup,bGroup = model(train_img, train_label, layers_dims,learning_rate=0.1, num_iterations=2000, print_cost=True)
# 对训练数据集进行预测
pred_train = predict(train_img,wGroup,bGroup)
print("预测准确率是: " + str(np.sum((pred_train == train_label) / train_img.shape[1])))
# 对测试数据集进行预测
pred_test = predict(test_img,wGroup,bGroup)
print("预测准确率是: " + str(np.sum((pred_test == test_label) / test_img.shape[1])))
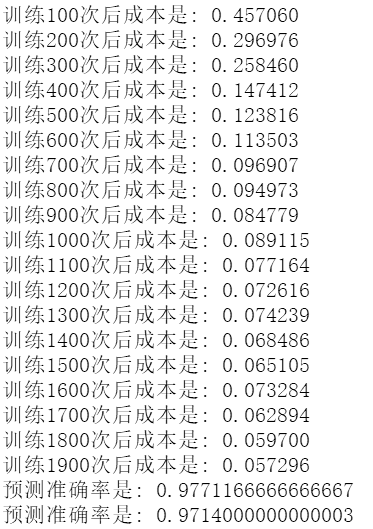
运行最后结果:
十、总结回顾
预测准确率较之前浅层神经网络又有了大幅的提升(之前是94%)。
其实从浅层神经网络开始,大部分都只是贴上代码了,有点”只可意会不可言传“的感觉,其实整体框架一直都没变,所以也不知道有啥可说的。后面我会继续花时间搞明白传播函数、反向传播函数的具体原理,到时再写深度解析的文章。
关注公众号“零基础爱学习”回复"AI6"可获得完整代码。后面我们还会继续更新“传播函数、反向传播函数的具体含义”,以及各种激活函数的区别。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号