《博弈入门》第二章:纳什均衡:理论
1 策略型博弈
策略型博弈是决策者之间相互作用的模型。正是因为相互作用,我们称决策者为局中人。每个局中人有一个可选行动的集合。模型中的每个局中人受到所有局中人行动的影响,而不仅是受到她自己行动的影响,从而获得局中人之间的相互作用。尤其是,每个局中人对于行动剖面一-所有局中人行动的列表(参见17.4节中关于剖面的讨论)---都有自己的偏好。
定义2.1(具有序数偏好的策略型博弈)(具有序数偏好的)策略型博弈由如下要素组成:
- 局中人集合
- 对于每个局中人,有一个行动集合
- 对于每一个局中人,有关于行动剖面集合的偏好
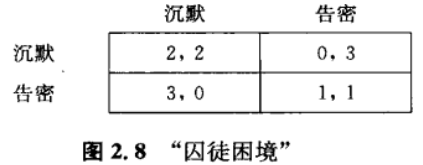
2.2 囚徒困境
2.2.1 合作项目
你和朋友合作-一个项目。你们每个人可以要么努力工作要么游手好闲。如果你的朋友努力工作,而你乐意游手好闲(如果你也努力工作的话,项目的结局将会好--些,可是其价值的增量对你来讲不值得付出额外的努力)。你喜欢你们俩都努力工作的结局甚于你们俩都游手好闲(在这种情况下,什么都没有完成),对于你,最差的结局是你工作很努力而你的朋友却游手好闲(你痛恨被“剥削")。如果你的朋友有相同的偏好,那么模拟你所面对情形的博弈将在图2.2中给出,如你所看到,这个博弈与“囚徒困境”的不同仅在于行动的名称。

我们并没有断言,两个人从事一个合作项目的情况必定具有“囚徒困境”的结构,只有当局中人的偏好与“囚徒困境”中一样时才是!例如,如果在其他人努力工作时每个人都喜欢努力工作甚于游手好闲,那么“囚徒困境”就不模拟这种情况:局中人的偏好与图2.2中给出的偏好不同。

| 努力工作 | 游手好闲 | |
| 努力工作 | 2,2 | 3,0 |
| 游手好闲 | 0,3 | 1,1 |
2.2.2 双寡头垄断

左图的博弈与“囚徒困境”的不同之处不仅在于局中人行动的名称,还在于其中两个局中人的偏好上有所不同。
右图的博弈与“囚徒困境”的不同之处仅在于局中人行动的名称。

| 随机 | 坚持 | |
| 随机 | 1/2(H+L),1/2(H+L) | L,H |
| 坚持 | H,L | S,S |
S>L
2.4 例证:匹配硬币(无冲突博弈)

2.6 纳什均衡
我们研究的求解理论有两个部分。首先,在给定关于其他局中人行动的信念下,每个局中人按照理性选择模型来选择自己的行动。其次,每个局中人关于其他局中人行动的信念是正确的。这两个部分包含在下面的定义中:


2.7 纳什均衡例子
囚徒困境

a.
| 沉默 | 告密 | |
| 沉默 | 4,4 | 3,3 |
| 告密 | 3,3 | 2,2 |
不是囚徒困境
b. 当a<1时,是“囚徒困境”
不是“囚徒困境”时,纳什均衡为(沉默,沉默)
2.7.8 严格和非严格均衡

2.8 最优反应函数
2.8.1 定义
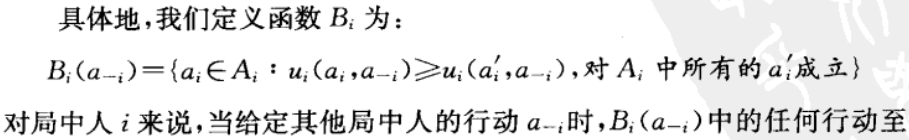

2.8.2 使用最优反应函数定义纳什均衡
我们可以另外定义纳什均衡是这样的行动剖面:每一个局中人的行动是关于其他局中人行动的最优反应。也就是说,我们有如下结果:

2.9 劣行动
2.9.1 严优
在任何博弈中,假如不管其他局中人如何做,局中人的一个行动比另--个行动总是优越些,那么这个行动“严优”于另一个行动。

严劣行动不是对于其他局中人的任何行动的-一个最优反应:无论其他局中人做什么,总有某些行动比“严劣行动”更好一些。因为局中人的纳什均衡是关于其他局中人的纳什均衡行动的最优反应,所以有:
严劣行动不使用于任何纳什均衡。
2.9.2 弱优
在任何博弈中,一个局中人的行动“弱优”于另一个行动,如果不管其他局中人怎样做,第一个行动至少像第二个行动一样好,并且对于其他局中人的某些行动,第一个行动好于第二个行动。
在严格纳什均衡(2.7.8节)中,没有一个局中人的均衡行动是弱劣的:对于每一个局中人,每个非均衡行动的盈利小于她的均衡盈利,所以没有一个非均衡行动弱优于她的均衡行动。
在非严格纳什均衡中的行动可能是弱劣的吗?答案是肯定的。

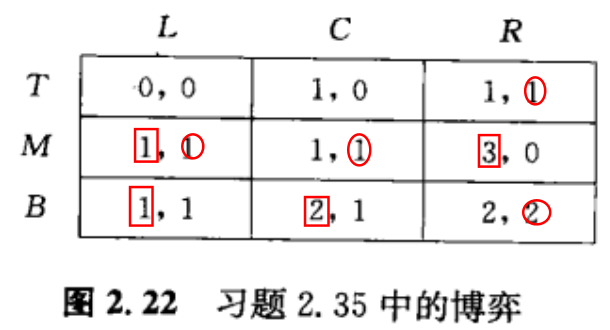
对于左侧局中人的弱劣行动为T
纳什均衡为(M,L)不是严格纳什均衡。u(M,L)=u(M,C)
2.9.3 例证:选举
两个候选人A和B竞选一份公职。共有奇数个市民投票,每个人可以投票给任何一位候选人。(弃权是不可能的。)获得多数票的候选人获胜。(由于市民数是奇数,因此不可能是平局。)大多数市民乐意A获胜。
下面的策略型博弈是针对这种情况下的市民投票决策所建立的模型。
局中人 市民
行动 每个局中人的行动集包含 了投票给A和投票给B。
偏好 对于大多数人投票给A的所有行动剖面,所有局中人都认为它们没有什么差别;同样,对于大多数人投票给B的所有行动剖面,所有局中人也都认为它们之间没有什么差别。一些局中人(大多数)喜欢第一种类型的行动剖面甚于第二种类型,而另一些人则有相反的偏好。
我们断言,市民投票给她不太喜欢的候选人弱劣于投票给她最喜欢的候选人。假如市民i喜欢候选人A ;并且,除i以外的其他所有市民的选票固定不变。如果市民i将她投给B的选票转而投给A,那么,考虑到其他市民的投票,要么结局不发生变化,要么使得A胜出而不是B胜出;这样一个转变不会使得赢者从A变为B。也就是说,市民i原先投给B的选票转向投给A,要么对结局没有影响,要么使她自己境况更好;但不可能使她境况更糟。
博弈中包含这样的纳什均衡,在这些均衡中,一些或者所有市民的行动是弱劣的。例如,所有市民选举B的行动剖面是一个纳什均衡( 没有一个市民的投票转移会对结局有任何影响)。
2.10 单一总体中的均衡:对称博弈和对称均衡
策略型博弈的纳什均衡对应于若干总体的成员之间相互作用的稳定状态。
这里,我们仅限于每次相互作用包含两个参与者的情况。定义一个两人博弈为“对称的”,如果每个局中人有相同的行动集,以及每个局中人对结局的评价仅依赖于她和对手的行动,不取决于她是局中人1还是局中人2。也就是说,局中人1对于她的行动是a1而其对手的行动是a2的结局(a1,a2)的感受,与局中人2对于她的行动是a1和其对手的行动是a2的结局(a2,a1)的感受是相同的。特别地,局中人的偏好可以用这样的盈利函数来描述,每当局中人选择相同的行动时,两个局中人的盈利是相同的:对于每一个行动a,u1(a,a)=u2(a,a)。


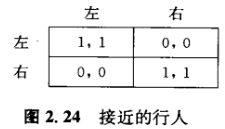
作为一个例子,考虑一个正在接近的行人的模型。在任意给定的遭遇中,每个参与者有两个可能的行动一朝右或者朝左一当参与者都以同样的方向行走,她们的境况好于她们以不同的方向行走(在后一种情况,会发生相撞)。这个例子所产生的对称的策略型博弈在图2. 24中给出。博弈有两个对称的纳什均衡,即(左,左)和(右,右)。也就是说,有两个稳定状态,其中一个状态是当遇到另一个行人时,每个行人都沿左边走,而另一个状态则是双方都沿右边走。
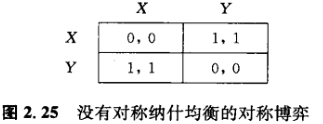
对称博弈可以没有对称的纳什均衡。例如,考虑图2. 25中的博弈。这个博弈有两个纳什均衡(X ,Y)和(Y ,X) ,其中没有一个是对称的。你可能想知道在这样的情形下,是否存在一个在每次相互作用时每个局中人总是不采用相同行动的稳定状态。这个问题将在4. 7节中进行分析。
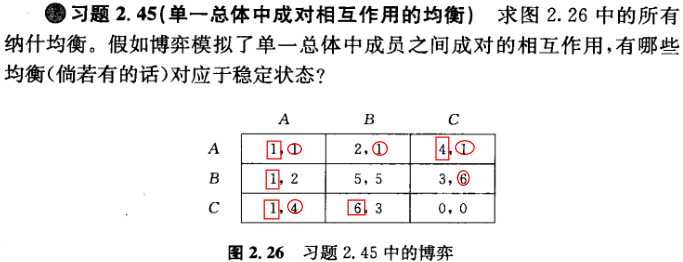
纳什均衡:(A,A)(A,C) (C,A)
(A,A)对应于稳定状态

