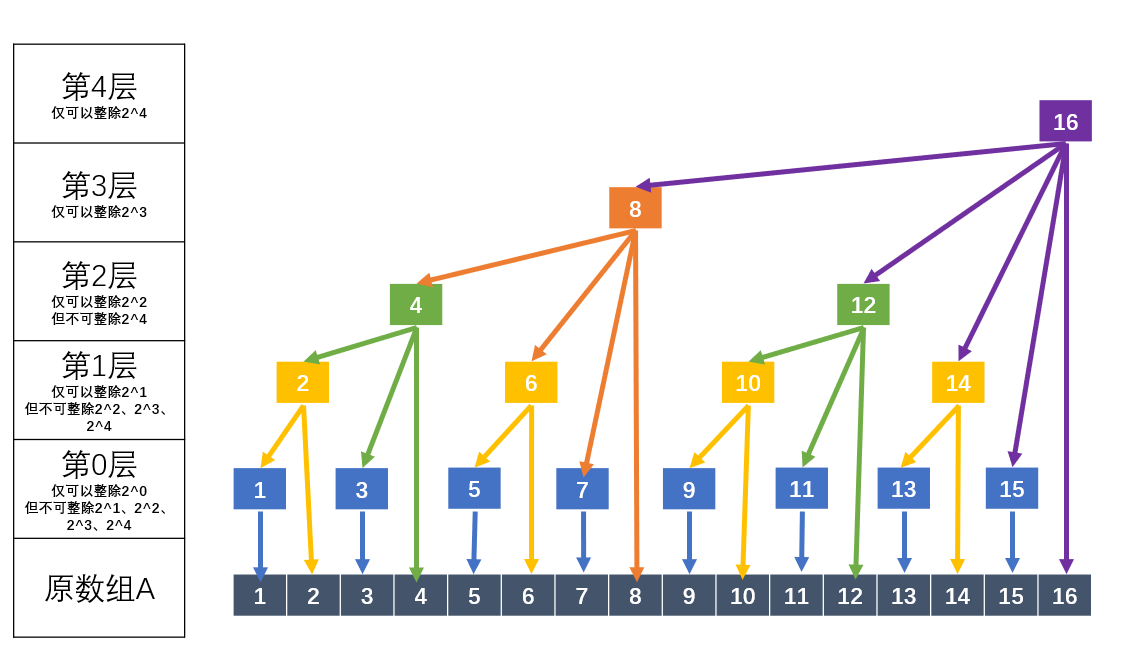
树状数组本质是什么呢?其实是二进制数。例如6如果用二进制数来表示6=0110=4+2 , 13=1101=8+4+1 . 因此我们可以用一个c[]数组来表示管辖范围,c[13]=c[13]+c[12]+c[8]. 那么求1~13的和就不用a[1]+a[2]+…a[13]了,而是可以直接c[13]+c[12]+c[8]。
我们可以看出刚才的13是1101有8,4,1构成,倒序来写就是13=1+4+8。我们可以先把1减掉,12=4+8,再把4减掉,8=8,再把8减掉8-8=0.这样一步一步求和运算。对应的1,4,8就是末尾1对应的位置,也就是大牛博客里讲到的Lowbit=x & (-x).这里不赘言。
找子节点(程序中不涉及找子节点的过程):
12(1100)是哪些节点的父节点
1.12(1100)管辖范围是4,所以子节点在8到12之间。
2.将12-1得到11(1011,第一个子节点)
3.11(1011)的管辖范围是1,减掉得到10(1010)
4.10(1010)的管辖范围是2,减掉得到8(1000)
5.所以12的直接子节点是: 11,10找父节点:(那么如何能把a[]数组转换为c[]数组呢)?
1.父节点一定比自己x大,需要加多少的数字,即为父节点
2.父节点-管辖范围<=x-lowbit(x)
这样看来,我们可以找到规律,如果在x末尾1后面加1,必然管辖范围就是刚刚加的1对应的十进制,减掉管辖范围,肯定不满足条件2
例如:x=1010(10)
最后一位加1变成1011假设是x的父节点,因此它的父节点管辖范围就是1,1011-0001=1010(10),还是它自己。
显然不满足 1010 <= 1010-lowbit(1010)=1000 (它自己减一个正数)
再如:x=10100
同样,往末位1的后面加1,则减掉管辖范围是x。也不满足 10100 <= 10100 - lowbit(10100)。
相同的道理,如果在倒数第二位加1,父节点为10110, 减掉lowbit(10110),依然不满足 <= 10100-lowbit(10100).
那么,哪一个才是比x本身大的第一个数字,且x末尾1的后面几位都不是1?
例如,x=10100
10100 + 0011 + 1 = 11000
即 x += lowbit(x)lowbit//-x=取反+1
int lowbit(int x){ return x&(-x); }
构建父节点c[]
void update(int p,int x){ while(p<=n){ c[p]+=x; p+=lowbit(p); } }
区间求和
int sum(int p){ int sum=0; while(p>0){ sum+=c[p]; p-=lowbit(p); } return sum; }
P3374 【模板】树状数组 1
如题,已知一个数列,你需要进行下面两种操作:
-
将某一个数加上 x
-
求出某区间每一个数的和
#include<iostream> #include<cstdio> #include<cmath> #include<cstring> using namespace std; int n,m,c[500005]; int lowbit(int x){ return x & (-x); } void add(int i,int x){ while(i <= n){ c[i] += x; i += lowbit(i); } } int sm(int i){ int sum = 0; while(i){ sum += c[i]; i -= lowbit(i); } return sum; } int main(){ scanf("%d%d",&n,&m); int v; for(int i = 1; i <= n; i++){ scanf("%d",&v); add(i,v); } int p,x,y,sl,sr; for(int i = 1; i <= m; i++){ scanf("%d%d%d",&p,&x,&y); if(p == 1){ add(x,y); } if(p == 2){ sr = sm(y); sl = sm(x - 1); printf("%d\n",sr - sl); } } return 0; }
&最长上升子序列 LIS(权值数状数组)
数值作为下标,比如当前是5,需要从1~4取找最大值,+1就是f[i]。
#include <bits/stdc++.h> #define ll long long using namespace std; int a[1000005], b[1000005], f[1000005], n, k, c[1000005], ans; int lowbit(int x) { return x & (-x); } void update(int p, int x) { while (p <= k) { c[p] = max(c[p], x); p += lowbit(p); } } int query(int x) { int mx = 0; while (x) { mx = max(mx, c[x]); x -= lowbit(x); } return mx; } int main() { cin >> n; for (int i = 1; i <= n; i++) { cin >> a[i]; b[i] = a[i]; } sort(b + 1, b + n + 1); k = unique(b + 1, b + n + 1) - (b + 1); for (int i = 1; i <= n; i++) { int x = lower_bound(b + 1, b + k + 1, a[i]) - b; f[i] = query(x - 1) + 1; update(x, f[i]); ans = max(ans, f[i]); } cout << ans << endl; return 0; }
&AcWing 3662 最大上升子序列的和 https://www.acwing.com/problem/content/3665/
&逆序对
241. 楼兰图腾 https://www.acwing.com/problem/content/243/
分别统计i位置左边比a[i]小的数的个数m、右边比a[i]小的数的个数n,运用乘法原理:
1. 第一步从左边m个数中任选一个,有m种选法
2. 第二步从右边n个数中任选一个,有n种选法
权值树状数组,统计比自己大的和。
#include<iostream>
#include<cstdio>
#include<cstring>
#define ll long long
using namespace std;
int c[200005], a[200005], n, h[200005], l[200005];
ll res, ans;
int lowbit(int x){
return x & (-x);
}
void add(int i, int x){
for(; i <= n; i += lowbit(i))
c[i] += x;
}
int sum(int i){
int sm = 0;
for(; i; i -= lowbit(i))
sm += c[i];
return sm;
}
int main(){
scanf("%d",&n);
for(int i = 1; i <= n; i++)
scanf("%d",&a[i]);
for(int i = 1; i <= n; i++){
h[i] = sum(n) - sum(a[i]);
l[i] = sum(a[i]-1);
add(a[i], 1);
}
memset(c, 0, sizeof c);
for(int i = n; i >= 1; i--){
ans += 1ll * h[i] * (sum(n) - sum(a[i]));
res += 1ll * l[i] * sum(a[i]-1);
add(a[i], 1);
}
printf("%lld %lld",ans, res);
return 0;
} acwing

输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
Q 4
Q 1
Q 2
C 1 6 3
Q 2输出样例:
4
1
2
5#include<bits/stdc++.h>
#define ll long long
using namespace std;
int n, m, a[100005], p;
ll c[100005];
char s[3];
int lowbit(int i){
return i & (-i);
}
void add(int i, int x){
for(; i <= n; i += lowbit(i)){
c[i] += x;
}
}
ll sum(int i){
ll sm = 0;
for(; i; i -= lowbit(i)){
sm += c[i];
}
return sm;
}
int main(){
scanf("%d%d",&n,&m);
for(int i = 1; i <= n; i++){
scanf("%d",&a[i]);
}
for(int i = 1; i <= n; i++){
add(i, a[i] - a[i-1]);
}
for(int i = 1; i <= m; i++){
int l,r,x;
scanf("%s",s);
if(s[0] == 'Q'){
scanf("%d",&p);
printf("%lld\n",sum(p));
}
else{
scanf("%d%d%d",&l,&r,&x);
add(l, x);
add(r+1, -x);
}
}
return 0;
} MIS
题目描述
长度为m的递增子序列(M length Increase Subsequence),称为MIS。
求长度为n的序列,有多少个MIS。
子序列不需要在原序列中不需要连续,但要保证相对位置。
输入格式
第一行两个整数n和m
第二行n个整数,表示一个序列。
输出格式
输出MIS的个数,结果对20140921取余。
样例
输入
5 3
1 2 5 3 4
输出
5
数据范围与提示
样例解释:[1 2 5],[1 2 3],[1 2 4],[1 3 4],[2 3 4] 都是MIS。
对于30%的数据,n的范围[1,30],m的范围[1,10];
对于60%的数据,n的范围[1,500],m的的范围[1,50];
对于80%的数据,n的范围[1,1000],m的的范围[1,100],序列中的元素范围[1,n];
对于100%的数据,n的范围[1,10000],m的的范围[1,100],序列中的元素范围[1,109];
比较容易想到60分的做法:</br> g[i][k]表示第i位在此上升子序列中排k名的方案数</br> 则: g[i][k] += g[j][k-1], 其中a[i] > a[j], g[j][k-1]表示第j位的数字在此上升子序列中排k-1名 </br> ``` #include<bits/stdc++.h> #define int long long using namespace std; int n, m, a[5005], g[5005][5005], ans, res; signed main(){ scanf("%lld%lld",&n,&m); for(int i = 1; i <= n; i++) scanf("%lld",&a[i]); for(int i = 1; i <= n; i++) g[i][1] = 1; for(int i = 1; i <= n; i++){ for(int j = 1; j < i; j++){ for(int k = 2; k <= m; k++){ if(a[i] > a[j]){ g[i][k] += g[j][k-1]; } } } res = (res + g[i][m]) % 20140921; } printf("%lld\n",res % 20140921); return 0; } ``` 优化:考虑如果g[i][k]累加的过程如果可以log级别查询到(求和),则总时间复杂度降为nlogn</br> 思考:当枚举到第p位时,在p-1位以前,比a[p]小且在此子序列中排名j的方案数之和,用树状数组维护"和":</br> 修改:数值i在子序列中排名为j的树状数组f[i][j]依次向上累加其方案数。</br> ``` void add(int i, int j, int x){ for(; i <= n; i += lowbit(i)){ g[i][j] = (g[i][j] + x) % 20140921; } } ``` 查询:查询权值小于等于i,且排名为j的方案数 ``` int query(int i, int j){ int sum = 0; for(; i; i -= lowbit(i)){ sum = (sum + g[i][j]) % 20140921; } return sum % 20140921; } ``` 权值树状数组,需要用到离散化。</br> 完整代码如下:</br> ``` #include<bits/stdc++.h> #define ll long long using namespace std; int g[10005][105], n, m, a[10005], b[10005]; int lowbit(int x){ return x & (-x); } void add(int i, int j, int x){ for(; i <= n; i += lowbit(i)){ g[i][j] = (g[i][j] + x) % 20140921; } } int query(int i, int j){ int sum = 0; for(; i; i -= lowbit(i)){ sum = (sum + g[i][j]) % 20140921; } return sum % 20140921; } int main(){ scanf("%d%d",&n,&m); for(int i = 1; i <= n; i++){ scanf("%d",&a[i]); b[i] = a[i]; } sort(b+1, b+n+1); int k = unique(b+1, b+n+1) - (b+1); for(int i = 1; i <= n; i++){ int x = lower_bound(b+1, b+k+1, a[i]) - b; add(x,1,1);//权值下标,排位,+1。每个数字自己作为上升序列的第一个位,其中排名就为1 for(int j = 2; j <= m; j++){ int sum = query(x-1, j-1);//查询权值比x小的,且排名为j-1的方案数 add(x, j, sum);//权值x排名为j的下标,排j-1位,+sum } } printf("%d\n",query(k,m) % 20140921); return 0; } ```
1376 最长递增子序列的数量
http://www.51nod.com/Challenge/Problem.html#problemId=1376
数组A包含N个整数(可能包含相同的值)。设S为A的子序列且S中的元素是递增的,则S为A的递增子序列。如果S的长度是所有递增子序列中最长的,则称S为A的最长递增子序列(LIS)。A的LIS可能有很多个。例如A为:{1 3 2 0 4},1 3 4,1 2 4均为A的LIS。给出数组A,求A的LIS有多少个。由于数量很大,输出Mod 1000000007的结果即可。相同的数字在不同的位置,算作不同的,例如 {1 1 2} 答案为2。
输入
第1行:1个数N,表示数组的长度。(1 <= N <= 50000) 第2 ~ N+1行:每行1个数A[i],表示数组的元素(0 <= A[i] <= 10^9)
输出
输出最长递增子序列的数量Mod 1000000007。
输入样例
5
1
3
2
0
4
输出样例
2
https://dandelioncloud.cn/article/details/1453017587545395202
//单点修改, 区间维护两个值,LIS以及最大 // #include<bits/stdc++.h> #include<iostream> #include<cstdio> #define N 500005 using namespace std; const int P = 1e9+7; struct Node{ int len, cnt; }c[N], dp[N]; int a[N], b[N], n, k; int lowbit(int x){ return x & (-x); } void update(Node &tmp, Node vl){ if(tmp.len == vl.len){ tmp.cnt += vl.cnt, tmp.cnt %= P; }else if(tmp.len < vl.len){ tmp = vl; } } void add(int i, Node vl){ for(; i <= k; i += lowbit(i)){ update(c[i], vl); } } Node query(int i){ Node mx = (Node){0, 1};//一开始写的(Node){0,0} for(; i; i -= lowbit(i)){ update(mx, c[i]); } return mx; } int main(){ scanf("%d",&n); for(int i = 1; i <= n; i++){ scanf("%d",&a[i]); b[i] = a[i]; } sort(b+1, b+n+1); k = unique(b+1, b+n+1) - (b+1); for(int i = 1; i <= n; i++){ a[i] = lower_bound(b+1, b+k+1, a[i]) - b; dp[i] = query(a[i]-1); dp[i].len++; add(a[i], dp[i]); //单点修改: 以它结尾的LIS长度, 相同长度的序列个数1 } Node ans = query(k);//query(n)一开始写的n printf("%d\n", ans.cnt); // Node ans = (Node){0,0}; // for(int i = 1; i <= n; i++){ // update(ans, dp[i]); // } // printf("%d\n",ans.cnt); return 0; }
abc_368G [ABC368G] Add and Multiply Queries
G:
# [ABC368G] Add and Multiply Queries
给定两个长度为 $ N $ 的正整数序列 $ A, B $。需要处理 $ Q $ 个按顺序给出的查询。查询有以下三种类型:
- 类型 $ 1 $:格式为 `1 i x`。将 $ A_i $ 替换为 $ x $。
- 类型 $ 2 $:格式为 `2 i x`。将 $ B_i $ 替换为 $ x $。
- 类型 $ 3 $:格式为 `3 l r`。需要解决以下问题并输出答案:
- 初始时 $ v = 0 $。依次对 $ i = l, l + 1, \dots, r $ 进行操作,每次操作将 $ v $ 替换为 $ v + A_i $ 或 $ v \times B_i $。求最终能得到的 $ v $ 的最大值。
需要注意的是,输入中类型 $ 3 $ 的查询的答案保证在 $ 10^{18} $ 以下。
### 制約
- $ 1 \leq N \leq 10^5 $
- $ 1 \leq A_i \leq 10^9 $
- $ 1 \leq B_i \leq 10^9 $
- $ 1 \leq Q \leq 10^5 $
- 类型 $ 1 $, $ 2 $ 的查询中,$ 1 \leq i \leq N $
- 类型 $ 1 $, $ 2 $ 的查询中,$ 1 \leq x \leq 10^9 $
- 类型 $ 3 $ 的查询中,$ 1 \leq l \leq r \leq N $
- 类型 $ 3 $ 的查询中,输出值在 $ 10^{18} $ 以下
类型 3 的查询的答案保证在 $10^18$,约等于$2^62$,也就是$10^5$个数字中只有60多次大于2的情况,其余情况都是1.
这样的话,我们大多数连续的区间,都是要选择A序列进行相加。
可以吧B序列中非1的位置放入set中,每次找到1的区间,树状数组求和,快速加给v。B序列单独比较非1的情况。
一开始想不明白:
1.当前询问在上一个询问基础上加减(傻X)
2.错误:没有修改:b[loc] = x;
3.错误:v = max(v+a[pos], v*b[pos]); //写成 v+= ....
#include<bits/stdc++.h> #define int long long using namespace std; int n, a[100005],b [100005], c[100005], q, op, res; set<int> s; int lowbit(int x){ return x & (-x); } void update(int i, int x){ while(i <= 100005){// c[i] += x, i += lowbit(i); } } int sum(int i){//前缀和 int ans = 0; while(i){ ans += c[i]; i -= lowbit(i); } return ans; } int loc, x; signed main(){ cin>>n; for(int i = 1; i <= n; i++){ cin>>a[i]; update(i, a[i]); } for(int i = 1; i <= n; i++){ cin>>b[i]; if(b[i] > 1) s.insert(i); } // s.insert(n); cin>>q; for(int i = 1; i <= q; i++){ cin>>op>>loc>>x; if(op == 1){ update(loc, x - a[loc]); a[loc] = x; } else if(op == 2){ if(b[loc] == 1){ if(x != 1) s.insert(loc); } else{ if(x == 1) s.erase(loc); } b[loc] = x; } else{ int v = a[loc++], r = x;//第一个数字一定是加到v中 set<int>::iterator it = s.lower_bound(loc); while(loc <= r){ int pos = *it; v += sum(min(pos-1, r)) - sum(loc-1); if(pos > r) break; v = max(v+a[pos], v*b[pos]); //写成 v+= .... loc = pos+1; it++; } cout<<v<<endl; } } return 0; }
洛谷 P5156 [USACO18DEC]Sort It Out P
省选模拟题 https://www.luogu.com.cn/problem/solution/P5156


 浙公网安备 33010602011771号
浙公网安备 33010602011771号