floyed一个总是讲不清楚的算法

    在上述讲解中，举例所有点先经过1号点，##再经过2号点，得到一个经过1、2号点的最短路，比如4-3最短路是10。继续经过3号点、4号点...将所有点的最短路得到，因此经过的点的循环是在最外层的。
  那么问题来了，经过1、2、3...n号点是按照顺序经过的，那么如果先枚举所有点经过2号点，再经过1号点，得到的最短路和上述方式结果一样么?

  比如是这样的,我们把图形简单化，原来的1号点和2号点换一下位置：

  我们可以模拟这个过程，那么将得到先通过1号点修改了2-3的最短路，在代码第一行。然后求4-3最短路时，经过2号点，而2-3在经过1号点时已经被修改成了当前最优。因此经过的点的顺序是没有影响的。

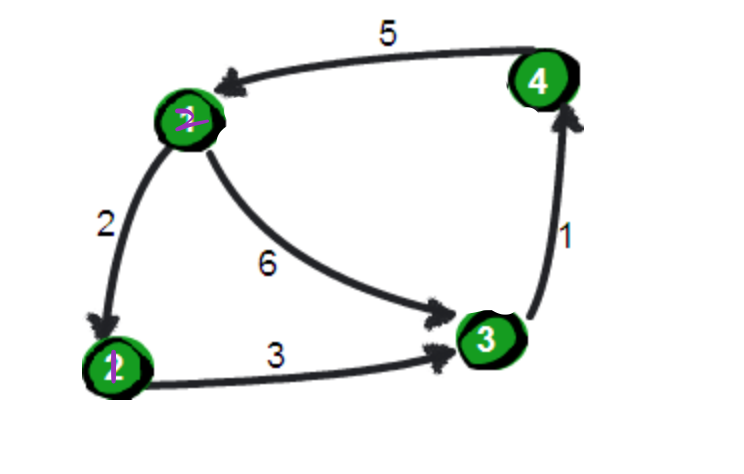
只经过1号点
** f[2][3] = min(f[2][1] + f[1][3], f[2][3]) = 5 **
f[2][4] = min(f[2][1] + f[1][4], f[2][4]) = ∞
f[3][2] = min(f[3][1] + f[1][4], f[3][2]) = ∞
f[3][4] = min(f[3][1] + f[1][4], f[3][4]) = 1 
f[4][2] = min(f[4][1] + f[1][2], f[4][2]) = 5
f[4][3] = min(f[4][1] + f[1][3], f[4][3]) = ∞

再累计经过2号点求最短
f[1][3] = min(f[1][2] + f[2][3], f[1][3]) = 3
f[1][4] = min(f[1][2] + f[2][4], f[1][4]) = ∞
f[3][1] = min(f[3][2] + f[2][1], f[3][1]) = ∞
f[3][4] = min(f[3][2] + f[2][4], f[3][4]) = 1
f[4][1] = min(f[4][2] + f[2][1], f[4][1]) = 7
**f[4][3] = min(f[4][2] + f[2][3], f[4][3]) = 5 + 5 =10**

dp[i][j][k] = min(dp[i][j][k-1], dp[i][k][k-1] + dp[k][j][k-1]);

为什么可以降维，因为下一个阶段比这个阶段更优。 dp[i][k][k] + dp[k][j][k]比dp[i][k][k-1] + dp[k][j][k-1]更优秀