欧拉路，欧拉回路
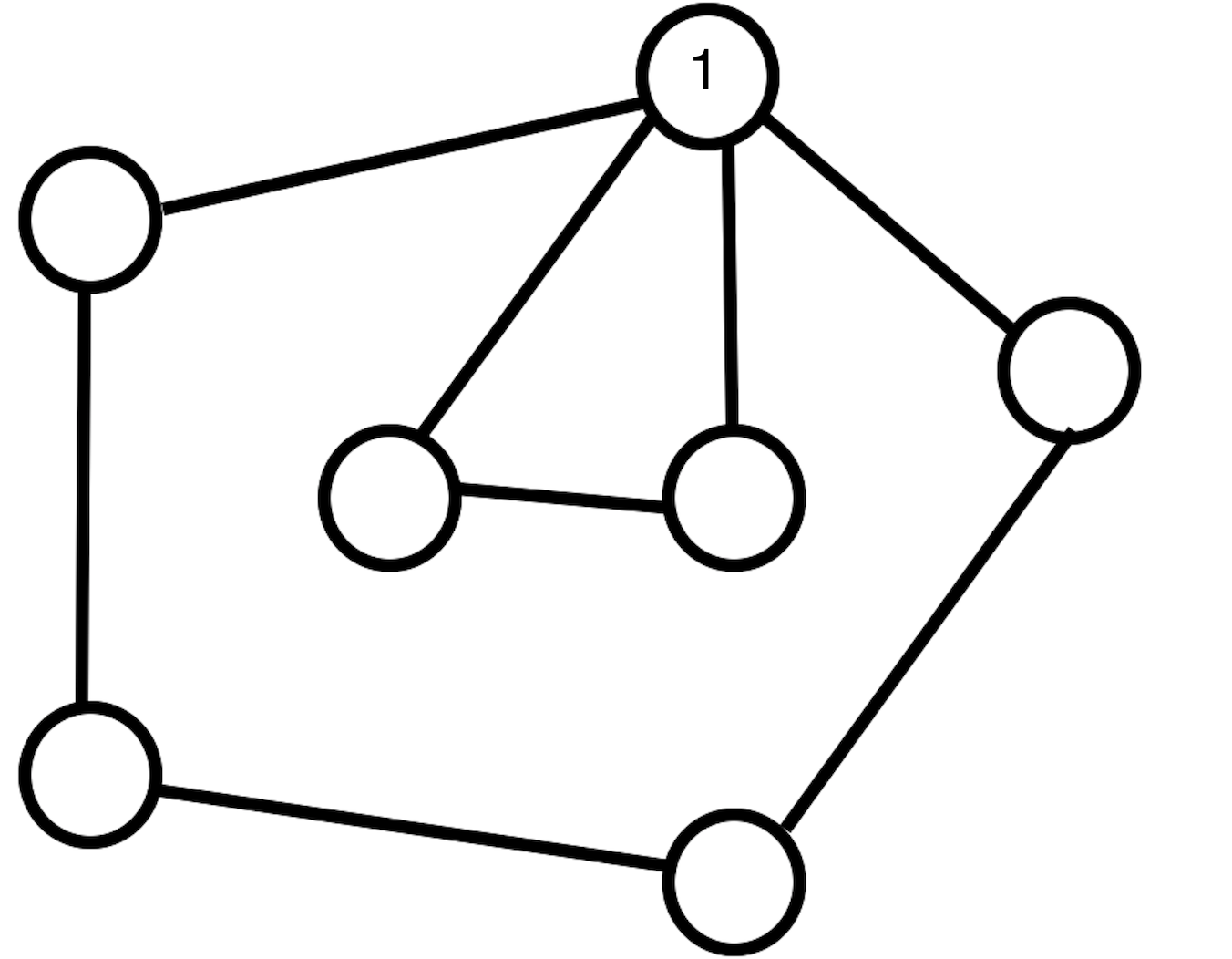
欧拉路指的是：存在这样一种图，可以从其中一点出发，不重复地走完其所有的边。下面哪些图是欧拉图？
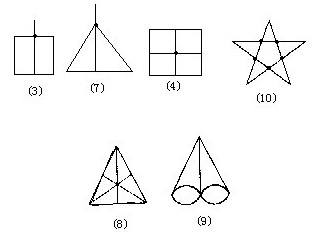
哪些是欧拉路或欧拉回路？
连通的无向图为（半）欧拉图的条件：
1.若所有顶点的度为偶数，则能够找到从任意顶点出发的欧拉回路。反之也成立，即若能够找到从任意顶点出发的欧拉回路，则所有顶点的度为偶数。
2.若有且仅有2个顶点的度数为奇数，则只能够找到欧拉路径（路径从这两点中的任一顶点出发，到另一顶点结束）。反之也成立。
连通的有向图为（半）欧拉图的条件：
1.若所有顶点的入度等于出度，则能够找到从任意顶点出发的欧拉回路。反之也成立。
2.若有且仅有两个顶点入度不等于出度，其中一个顶点入度比出度大1，记为V1，另一个顶点入度比出度小1，记为V2，则只能够找到欧拉路径（路径从顶点V2出发，到顶点V1结束）。反之也成立。
Hierholzer 算法
- 选择奇点为起点，遍历所有相邻边。
- 深度搜索，访问相邻顶点。将经过的边都删除，g[u][v]--,g[v][u]--。
- 如果当前顶点已经搜索完，则将顶点入栈。
- 栈中的顶点倒序输出，就是从起点出发的欧拉回路
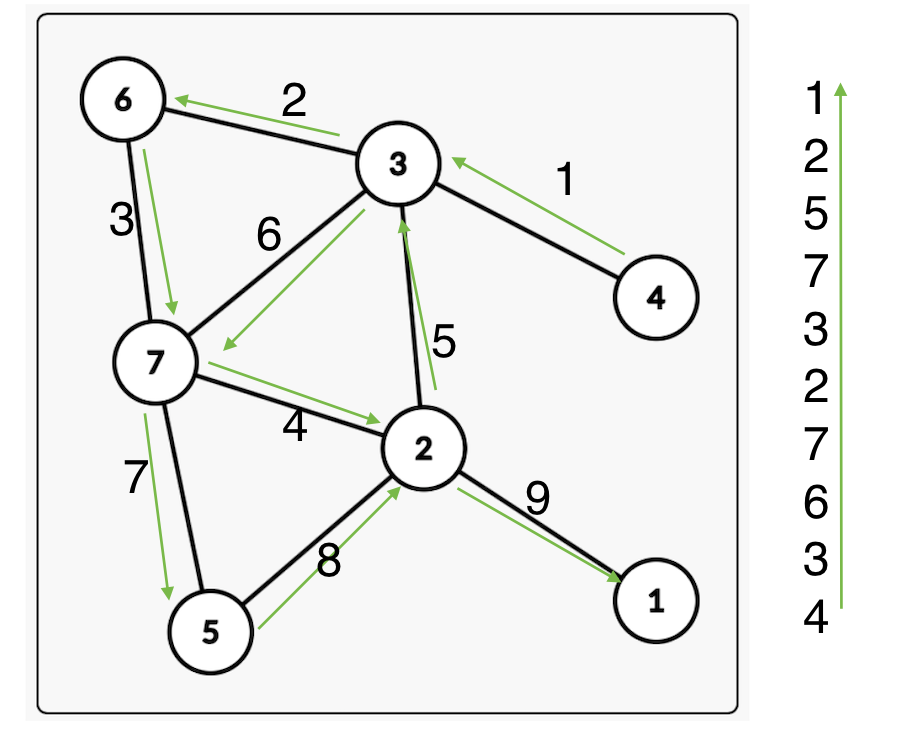
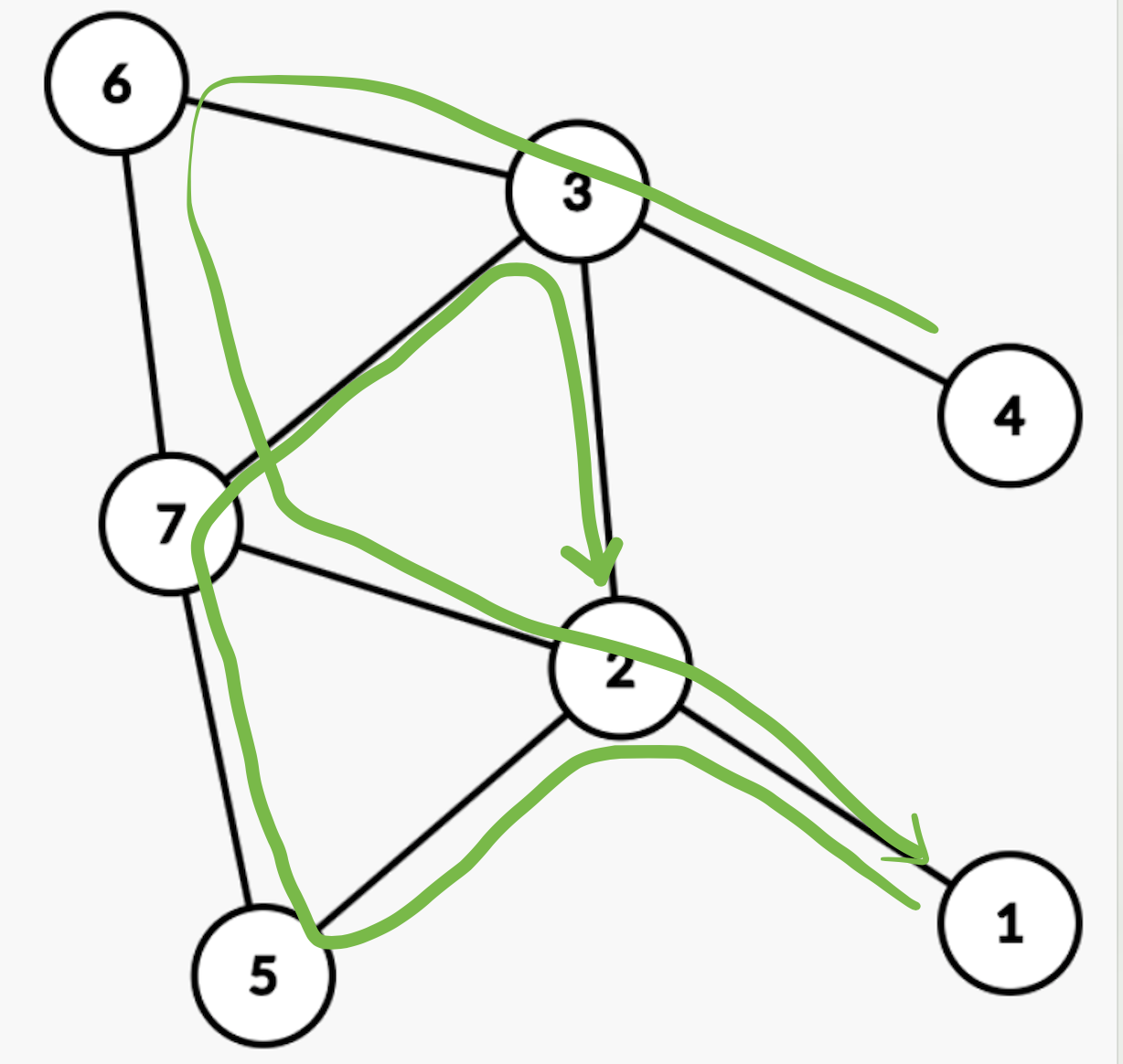
入栈顺序：1 2 3 7 5 2 7 6 3 4
什么时候入栈？ dfs到它没有出边了，或者回溯回来搜完了，都要入栈，比如2号点。
由于递归写法可能调用o(m)层系统栈，其中每层存储很多变量，可能会爆栈mle,因此选择非递归方式，具体看《算法进阶》
证明：
O 当遇到另一个出度等于入度的顶点V时，是不可能停留在V的，因为出度等于入度，你进入多少次，一定有对应的出边让你出去多少次。
O 因此第一个遇到的没有可遍历的顶点只有两种，一种是它的入度比出度大一，另一种是它的入度与出度相等，但是它是起点（也就是说既是起点又是终点，饶了一圈）。根据前面所说的一些结论（图与欧拉路径、欧拉回路的结论），这两种点都是某条欧拉路径上的终点，所以当我们遇到的没有可遍历的顶点，尽管放心大胆的把该顶点记录下来，因为它一定是欧拉路径的终点,设为v。
O 为什么遇到的第二个没有可遍历的邻居的顶点是欧拉路径倒数第二个点？
u->v将深搜边（深搜的合法路径）“删掉”后，该邻点u一定是个奇数点，对于删了边之后的新图，u就变成了唯一符合的终点。照此规律下去，就是倒着排列的欧拉序列。
例题：
P2731 [USACO3.3]骑马修栅栏 Riding the Fences
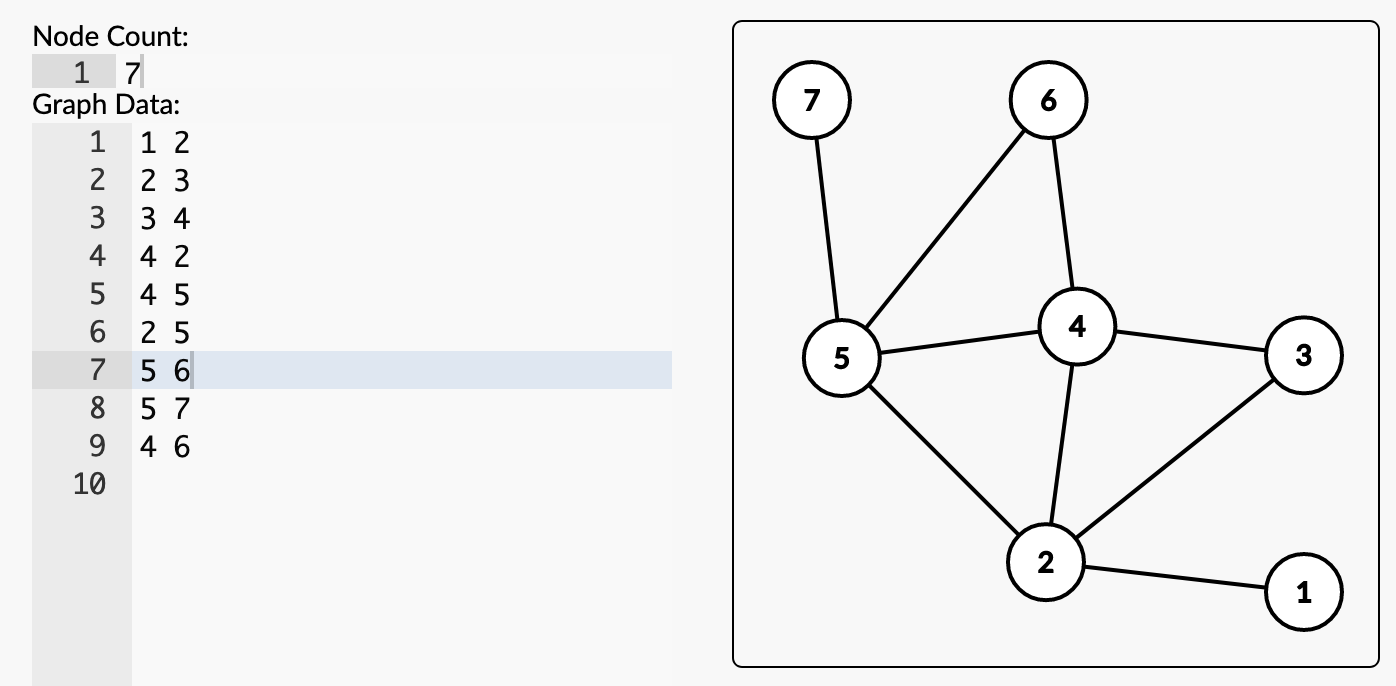
output:
1 2 3 4 2 5 4 6 5 7
下图是用邻接矩阵建图的，如果用邻接表建图该如何实现？考虑tarjan求桥的方法，f[i] = f[i^1] = 1;，但是本题只能用邻接矩阵，从编号小的点搜索，小的数一定最先用完边，这样
先入栈。
#include <cstdio>
#include <algorithm>
#include <iostream>
#include <stack>
using namespace std;
const int maxn = 1031;
int G[maxn][maxn], du[maxn];
int n,m;
stack<int> S;//用一个栈来保存路径
void dfs(int u)
{
for(int v=1; v<=n; v++)
if(G[u][v])
{
G[u][v]--;
G[v][u]--;
dfs(v);
}
S.push(u);
}
int main(){
cin>>m;
int u,v;
for(int i=1; i<=m; i++){
cin>>u>>v;
n = max(n,u);
n = max(n,v);
G[u][v]++;
G[v][u]++;
du[u]++;
du[v]++;
}//用邻接矩阵记录图
int s = 1;
for(int i=1; i<=n; i++)
if(du[i]%2==1)
{
s=i;
break;
}//寻找起点
dfs(s);
while(!S.empty()){
cout<<S.top()<<endl;
S.pop();
}
return 0;
}
如果不考虑字典序问题，递归代码和非递归代码如下代码：
#include <cstdio> #include <algorithm> #include <iostream> #include <stack> #include <cstring> using namespace std; const int maxn = 20005; int G[maxn][maxn], du[maxn],hd[maxn],f[maxn]; int n,m,cnt = -1; stack<int> S;//用一个栈来保存路径 struct Edge{ int to,nxt; }edge[50005<<1]; void add(int u, int v){ cnt++; edge[cnt].to = v; edge[cnt].nxt = hd[u]; hd[u] = cnt; } //多次经过 u,下一次dfs到这个点时，能够找到不重复的第一条边 void dfs(int u){ for(int i = hd[u]; ~i;i = edge[i].nxt){ if(f[i]) continue; f[i] = f[i^1] = 1; int v = edge[i].to; dfs(v); } S.push(u); } int main(){ memset(hd, -1, sizeof hd); scanf("%d",&m); int u,v; for(int i=1; i<=m; i++){ scanf("%d%d",&u,&v); n =max(v,max(n,u)) ; add(u,v); add(v,u); du[u]++; du[v]++; } int s = 1; for(int i=1; i<=n; i++) if(du[i]%2==1){ s=i; break; }//寻找起点 dfs(s); while(!S.empty()){ cout<<S.top()<<endl; S.pop(); } return 0; }
#include<bits/stdc++.h> using namespace std; int hd[10005],cnt = 1, vis[10005],t, ans[10005],m,n, du[10005]; stack<int> q; struct Edge{ int to,nxt; }edge[200005]; void add(int u, int v){ cnt++; edge[cnt].to = v; edge[cnt].nxt = hd[u]; hd[u] = cnt; } void work(int s){ q.push(s); while(!q.empty()){//取栈顶元素 int u = q.top(); int i = hd[u]; while(i && vis[i]) i = edge[i].nxt; if(i){ int v = edge[i].to; q.push(v);s vis[i] = vis[i^1] = 1; }else{ ans[++t] = u; q.pop(); } } } int main(){ scanf("%d%d",&n,&m); int u,v; for(int i=1; i<=m; i++){ scanf("%d%d",&u,&v); add(u,v); add(v,u); du[u]++; du[v]++; } int ss; for(int i=1; i<=n; i++) if(du[i]%2==1){ ss=i; break; } cout<<ss<<endl; work(ss); for(int i = t; i >= 1; i--) printf("%d ",ans[i]); return 0; } /* 7 9 1 2 2 3 3 4 4 2 4 5 2 5 5 6 5 7 4 6 */
P1341 无序字母对
#include<cstdio> #include<cstring> int a[106],c[10006],du[101],n,x,y,t,k=0xfffffff,tot; bool b[106][106]; char s[2]; int min(int u,int v) { return u<v ? u:v; } void dfs(int u) { for(int i=0; i<58; i++)/*A到z之间还有一些字符，总共58个*/ { if(b[u][i]) { b[u][i]=b[i][u]=0; dfs(i); } } c[++tot]=u; } int main() { scanf("%d",&n); for(int i=1; i<=n; i++) { scanf("%s",&s); x=s[0]-'A'; y=s[1]-'A';/*字符串从零开始读入*/ k=min(k,min(x,y)); b[x][y]=b[y][x]=1; du[x]++; du[y]++; } for(int i=0; i<58; i++) if(du[i]%2==1) a[++t]=i; if(t==0) dfs(k); else if(t==2) dfs(a[1]); else { printf("No Solution\n"); return 0; } for(int i=tot; i>=1; i--) printf("%c",c[i]+'A'); return 0; }
P3520 [POI2011]SMI-Garbage
给定n个点m条边，每条边有一个初始权值0或1，有一个最终权值0或1，每次可以给一个简单环上的边权值异或1，求一种方案使得每条边从初始权值变成最终权值，无解输出"NIE"
解析：没有变化的边不加入图的建立，欧拉图的本质就是每个边走一次，完全欧拉图就是一个个环构成，那么没有奇数点，则可以判断nie，或者求出可行解（通过深搜放到栈中，倒序输出即可）。
输出格式：（若干简单环）
环的边数 简单环上的点
环的边数 简单环上的点
... ...
为什么下面的代码需要循环直到du[i]为0？比如如下环，1号点找完第一个简单环后，还有一个简单环，因此需要while()直到1号点度为0结束：
#include<iostream> #include<stdio.h> #include<string.h> using namespace std; int first[5000001],next[5000001],to[5000000],du[5000000],f[5000000]; int c[1000000],d[10000000];//c所有访问顺序,用d来分隔 int tot=0,n,m,cnt=0; void add(int x,int y) { next[tot]=first[x]; first[x]=tot; to[tot]=y; tot++; } void dfs(int x,int r) { d[cnt++]=x; du[x]-=2; for(int i=first[x];i>-1;i=next[i]) { if(f[i])continue; //边号tot是从0开始的,所以i和i^1恰好为正反边 f[i]=1; f[i^1]=1; if(to[i]==r) { //起点多记录一次 d[cnt++]=r; return; } dfs(to[i],r); //每个点每次只会走一条边所以可以直接return掉 return; } } int main() { memset(first,-1,sizeof(first)); memset(next,-1,sizeof(next)); memset(du,0,sizeof(du)); cin>>n>>m; for(int i=0;i<m;i++) { int x,y,z1,z2; cin>>x>>y>>z1>>z2; if(z1!=z2) { //正反加边 add(x,y); add(y,x); du[x]++; du[y]++; } } for(int i=1;i<=n;i++) if(du[i]%2==1) { cout<<"NIE"; return 0; } int cou=0; for(int i=1;i<=n;i++) { while(du[i]) { dfs(i,i); cou++; c[cou]=cnt; } } /*cout<<"------"; for(int i=0;i<cnt;i++) { cout<<d[i]<<" "; } cout<<"------"<<endl; for(int i=0;i<cou;i++) { cout<<c[i]<<" "; } cout<<"------"<<endl;*/ int j=0; cout<<cou<<endl; for(int i=1;i<=cou;i++) { cout<<c[i]-c[i-1]-1<<" "; while(j<c[i]) { cout<<d[j]<<" "; j++; } cout<<endl; } return 0; #include<iostream>
for(int i=1;i<=n;i++){
while(du[i]){
num++; dfs(i,i);
}
}
#include<stdio.h>
#include<string.h>
#include<vector>
using namespace std;
int head[5000005],nxt[5000005],to[5000005],du[5000005],f[5000005];
int c[10000005],num=0;;//c所有访问顺序,用d来分隔
vector<int> d[100005];
int tot=0,n,m,cnt=0;
void add(int x,int y){
nxt[tot]=head[x];
head[x]=tot;
to[tot]=y;
tot++;
}
void dfs(int x,int r){
d[num].push_back(x);
du[x]-=2;
for(int i=head[x];i>-1;i=nxt[i]){
if(f[i])continue;
f[i] = f[i^1] = 1;
if(to[i]==r){
d[num].push_back(r);
return;
}
dfs(to[i],r);//每个点每次只会走一条边所以可以直接return掉
return;
}
}
int main(){
memset(head,-1,sizeof(head));
memset(nxt,-1,sizeof(nxt));
scanf("%d%d",&n,&m);
for(int i=0;i<m;i++){
int x,y,z1,z2;
cin>>x>>y>>z1>>z2;
if(z1!=z2){ //不同加边
add(x,y); add(y,x);
du[x]++; du[y]++;
}
}
for(int i=1;i<=n;i++)
if(du[i]%2==1) {
cout<<"NIE"; return 0;
}
for(int i=1;i<=n;i++){
while(du[i]){
num++; dfs(i,i);
}
}
printf("%d\n",num);
for(int i = 1; i <= num; i++){
printf("%d ",d[i].size()-1);
for(int j = 0; j < d[i].size(); j++)
printf("%d ",d[i][j]);
printf("\n");
}
return 0;
}
753.破解保险箱 https://leetcode-cn.com/problems/reconstruct-itinerary/
https://leetcode-cn.com/problems/reconstruct-itinerary/
