Fibonacci sequence
1133. Fibonacci Sequence
Time Limit: 1.0 second
Memory Limit: 16 MB
Memory Limit: 16 MB
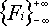
is an infinite sequence of integers that satisfies to Fibonacci conditionFi + 2 = Fi + 1 + Fi for any integer i. Write a program, which calculates the value of Fn for the given values of Fi and Fj.
Input
The input contains five integers in the following order: i, Fi, j, Fj, n.
−1000 ≤ i, j, n ≤ 1000, i ≠ j,
−2·109 ≤ Fk ≤ 2·109 (k = min(i, j, n), …, max(i, j, n)).
−1000 ≤ i, j, n ≤ 1000, i ≠ j,
−2·109 ≤ Fk ≤ 2·109 (k = min(i, j, n), …, max(i, j, n)).
Output
The output consists of a single integer, which is the value of Fn.
这题目最开始想到的解法是用搜索,由输入的Fi,Fj,求出与Fi相邻的另一个数Fj+1,再往后继续求,加上动态规划的话,复杂度也不算高。。。
但。。。就在准备动手搞的时候,意外发生了。我忽然觉得,或许可以数学方式来递推一下,于是,拿过纸笔在黄纸上算啊算啊。。。
一直没搞出来,算了,还是笨方法吧。
现在的做法就是直接搜索:
F(n) = F(n-1)+F(n-2)
现在输入是Fi,Fj,假设i < j.
现在我需要找到F(i+1).
很显然,对于任意的k > i.
Fk = xFi + yF(i+1).
只要求出x,y,问题就解决了。
要求出x,y,我只要求F(k-1),F(k-2)的x,y.
对了,这个需要做高精度的处理,x,y可能会很大很大。。。
static BigInt sx,sy; static BigInt sx2,sy2; static bool found[N]; static BigInt value[N][2]; static const int HALF = 1000; static void GetXY(int i,int k,BigInt& x,BigInt& y) { if(k == i) { y = 0; x = 1; return ; } if(k == i+1) { x = 0; y = 1; return ; } int index = n + HALFT; if(found[index]) { x = value[index][0]; y = value[index][1]; return; } GetNext(i,k-1,sx,sy); GetNext(i,k-2,sx2,sy2); x = sx+sx2; y = sy+sy2; value[index][0] = x; value[index][1] = y; found[index] = true; return; }
int GetNextValue(int i,int fi,int j,int fj) { BigInt x,y; GetXY(i,j,x,y); return (fj - fi*x)/y; }





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· winform 绘制太阳,地球,月球 运作规律
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现