977.
暴力法:整个数组平方,然后再nums.sort(),时间复杂度O(nlogn) 空间复杂度O(1)
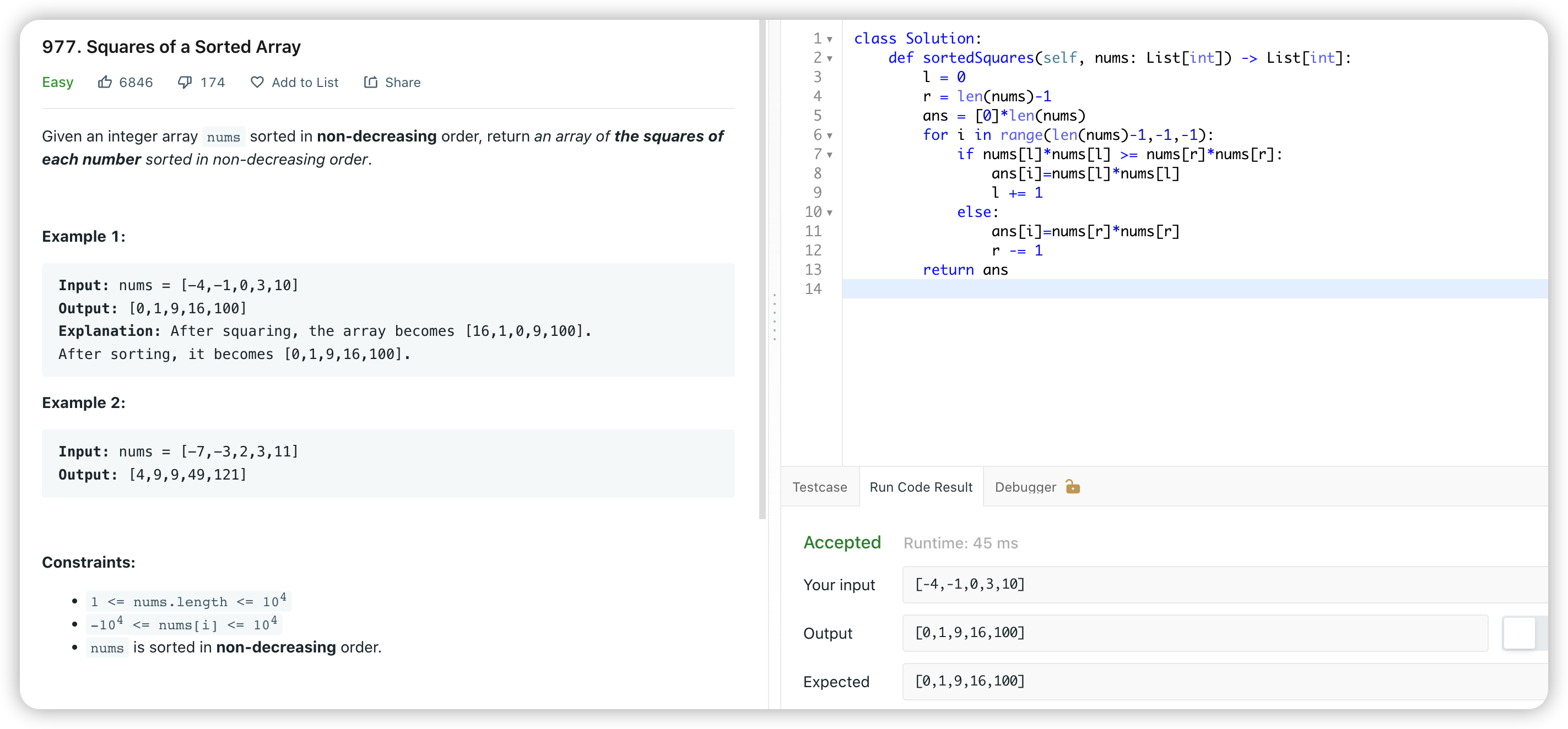
双指针法:从两头开始遍历,l,r指向当前有可能的最大值,i象征着新数组对应的位置,从大到小,时间复杂度:O(n), 空间复杂度:O(n)
209.
暴力法:两层for循环,第一个是起始位置,第二个是终止位置,把所有数组的情况都遍历一遍,找到最小的数组长度
class Solution: def minSubArrayLen(self, target: int, nums: List[int]) -> int: if nums == None or len(nums) == 0: return 0 if nums[0] >= target: return 1 minimum = float("inf") for i in range(len(nums)): subarray_sum = 0 for j in range(i,len(nums)): subarray_sum += nums[j] if j - i < minimum and subarray_sum == target: minimum = j - i + 1 if minimum == float("inf"): return 0 else: return minimum
滑动窗口:类似于双指针,取两个指针中间的集合,所以叫滑动窗口
重点一:j指向终止位置,i起始位置动态移动——一个for循环的思路才能解决
重点二:【精华】如何移动起始位置
——当集合元素和>=s 说明符合条件,收集其长度后,i可以往后移动,缩小集合范围看下一个集合是否符合条件
result = float('inf') 先取最大值 之后才能取所有集合里的最小值
i=0
for(j=0,j<=nums.size-1,j++)
Sum+=nums[j]
Sum>=s 这里的逻辑是while 持续更新
subL=j-i+1
result = min(result,subL)
Sum=Sum-nums[i]
i++
class Solution: def minSubArrayLen(self, s: int, nums: List[int]) -> int: # 定义一个无限大的数 res = float("inf") Sum = 0 i = 0 for j in range(len(nums)): Sum += nums[j] while Sum >= s: res = min(res, j-i+1) Sum -= nums[i] i += 1 return 0 if res==float("inf") else res
59.螺旋矩阵
循环不变量:
[) 或者 [] 坚持一个原则,左闭右开 坚持到底
我们不去处理每条边的最后一个节点,把最后一个节点留给下一条边
这样转一圈,坚持左闭右开的原则,每一个点都会遍历到
每一条边的处理规则要统一——循环不变量
class Solution: def generateMatrix(self, n: int) -> List[List[int]]: nums = [[0] * n for _ in range(n)] startx, starty = 0, 0 # 起始点 loop, mid = n // 2, n // 2 # 迭代次数、n为奇数时,矩阵的中心点 count = 1 # 计数 for offset in range(1, loop + 1) : # 每循环一层偏移量加1,偏移量从1开始 for i in range(starty, n - offset) : # 从左至右,左闭右开 nums[startx][i] = count count += 1 for i in range(startx, n - offset) : # 从上至下 nums[i][n - offset] = count count += 1 for i in range(n - offset, starty, -1) : # 从右至左 nums[n - offset][i] = count count += 1 for i in range(n - offset, startx, -1) : # 从下至上 nums[i][starty] = count count += 1 startx += 1 # 更新起始点 starty += 1 if n % 2 != 0 : # n为奇数时,填充中心点 nums[mid][mid] = count return nums



