Topic | Hyperparameter Optimization for Neural Networks
Post
Paper
Note
Introduction
Sometimes it can be difficult to choose a correct architecture for Neural Networks. Usually, this process requires a lot of experience because networks include many parameters. Let’s check some of the most important parameters that we can optimize for the neural network:
- Number of layers
- Different parameters for each layer (number of hidden units, filter size for convolutional layer and so on)
- Type of activation functions
- Parameter initialization method
- Learning rate
- Loss function
Even though the list of parameters in not even close to being complete, it’s still impressive how many parameters influences network’s accuracy.
Hyperparameter optimization
In this article, I would like to show a few different hyperparameter selection methods.
- Grid Search
- Random Search
- Hand-tuning
- Gaussian Process with Expected Improvement
- Tree-structured Parzen Estimators (TPE)
Grid Search
The simplest algorithms that you can use for hyperparameter optimization is a Grid Search. The idea is simple and straightforward. You just need to define a set of parameter values, train model for all possible parameter combinations and select the best one. This method is a good choice only when model can train quickly, which is not the case for typical neural networks.
Imagine that we need to optimize 5 parameters. Let’s assume, for simplicity, that we want to try 10 different values per each parameter. Therefore, we need to make 100,000 (105105) evaluations. Assuming that network trains 10 minutes on average we will have finished hyperparameter tuning in almost 2 years. Seems crazy, right? Typically, network trains much longer and we need to tune more hyperparameters, which means that it can take forever to run grid search for typical neural network. The better solution is random search.
Random Search
The idea is similar to Grid Search, but instead of trying all possible combinations we will just use randomly selected subset of the parameters. Instead of trying to check 100,000 samples we can check only 1,000 of parameters. Now it should take a week to run hyperparameter optimization instead of 2 years.
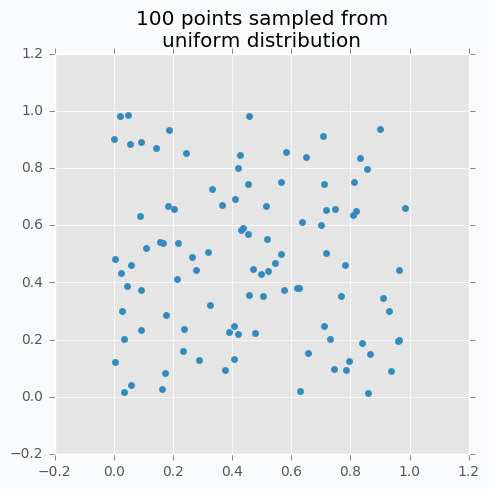
Let’s sample 100 two-dimensional data points from a uniform distribution.
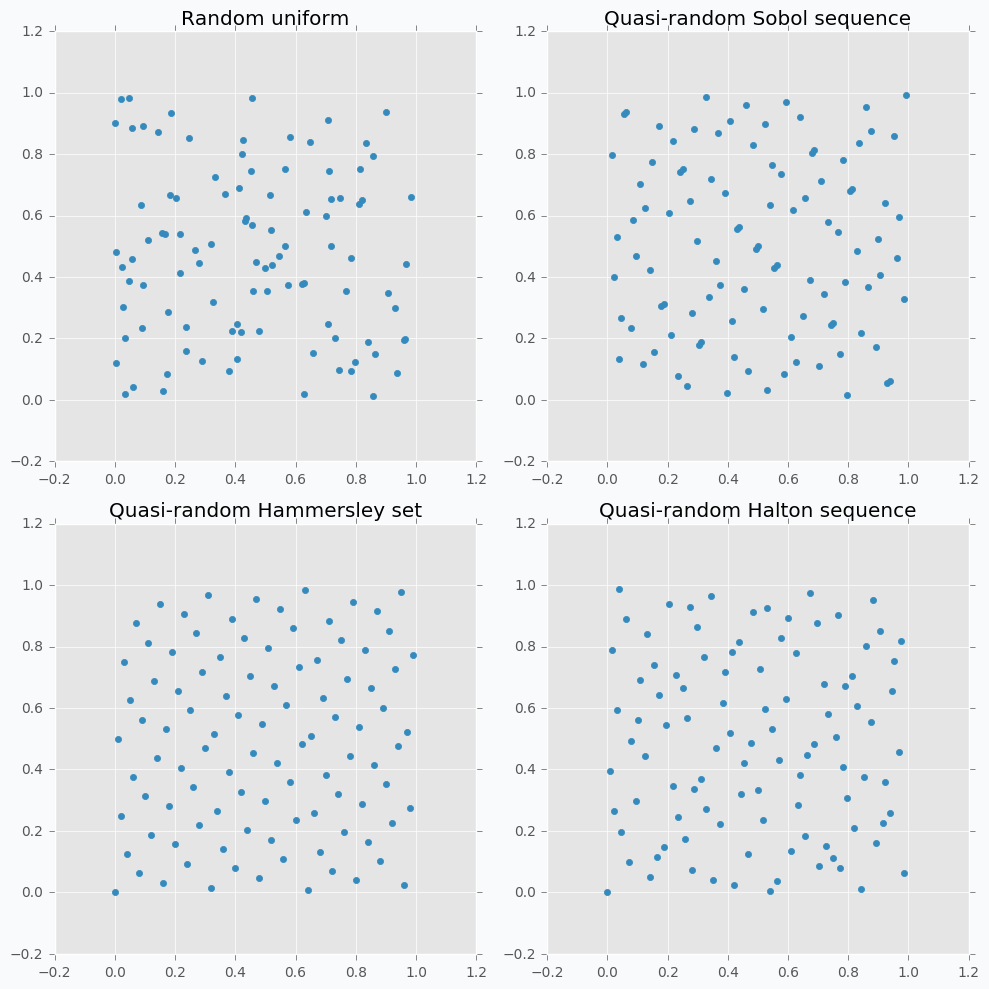
In case if there are not enough data points, random sampling doesn’t fully covers parameter space. It can be seen in the figure above because there are some regions that don’t have data points. In addition, it samples some points very close to each other which are redundant for our purposes. We can solve this problem with Low-discrepancy sequences (also called quasi-random sequences).
There are many different techniques for quasi-random sequences:
- Sobol sequence
- Hammersley set
- Halton sequence
- Poisson disk sampling
Let’s compare some of the mentioned methods with previously random sampled data points.
As we can see now sampled points spread out through the parameter space more uniformly. One disadvantage of these methods is that not all of them can provide you good results for the higher dimensions. For instance, Halton sequence and Hammersley set do not work well for dimension bigger than 10 [7].
Even though we improved hyperparameter optimization algorithm it still is not suitable for large neural networks.
But before we move on to more complicated methods I want to focus on parameter hand-tuning.
Hand-tuning
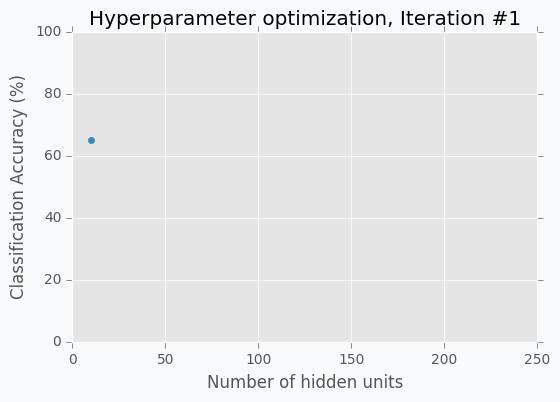
Let’s start with an example. Imagine that we want to select the best number of units in the hidden layer (we set up just one hyperparameter for simplicity). The simplest thing is to try different values and select the best one. Let’s say we set up 10 units for the hidden layer and train the network. After the training, we check the accuracy for the validation dataset and it turns out that we classified 65% of the samples correctly.
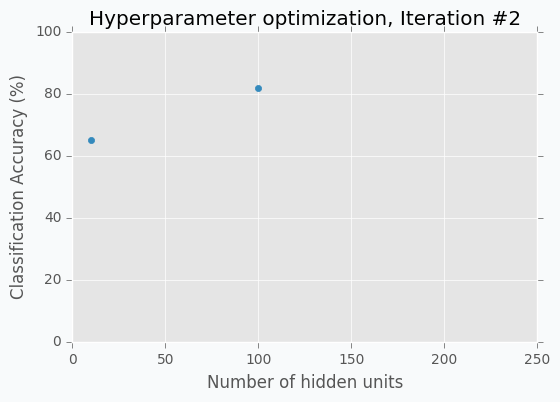
The accuracy is low, so it’s intuitive to think that we need more units in a hidden layer. Let’s increase the number of units and check the improvement. But, by how many should we increase the number of units? Will small changes make a significant effect on the prediction accuracy? Would it be a good step to set up a number of hidden units equal to 12? Probably not. So let’s go further and explore parameters from the next order of magnitude. We can set up a number of hidden units equal to 100.
For the 100 hidden units, we got prediction accuracy equal to 82% which is a great improvement compared to 65%. Two points in the figure above show us that by increasing number of hidden units we increase the accuracy. We can proceed using the same strategy and train network with 200 hidden units.
After the third iteration, our prediction accuracy is 84%. We’ve increased the number of units by a factor of two and got only 2% of improvement.
We can keep going, but I think judging by this example it is clear that human can select parameters better than Grid search or Random search algorithms. The main reason why is that we are able to learn from our previous mistakes. After each iteration, we memorize and analyze our previous results. This information gives us a much better way for selection of the next set of parameters. And even more than that. The more you work with neural networks the better intuition you develop for what and when to use.
Nevertheless, let’s get back to our optimization problem. How can we automate the process described above? One way of doing this is to apply a Bayesian Optimization.
Other Reference




 浙公网安备 33010602011771号
浙公网安备 33010602011771号