经典图像增强算法总结

背景

在采集或传递图像的过程中常会受到各种噪声的影响，这会导致其中包含的重要信息很难被读取和识别。例如，不均匀的光照会使图像灰度过于集中；摄像头的数模转换电路所产生的噪声会使图像质量降低；图像显示设备的局限性会造成图像显示颜色减少等。

因此，在对图像进行分析处理之前，必须对图像进行增强，使其更适合人或机器进一步分析处理。

介绍

图像增强是图像处理的一个重要分支。它针对给定图像的应用场合，通过各种算法增强图像中的有用信息，有目的地强调图像的整体或局部特性，抑制不感兴趣的区域，扩大图像中不同特征之间的差别，改善图像质量，加强图像判读和识别效果，使图像更能满足分析或机器决策的需要。

图像增强一般并不能增加原图像信息，但是能针对一些成像条件，突出微弱信号，使信息更容易分辨。图像增强算法根据处理过程所在的空间不同，可分为基于空间域的算法和基于频率域（变换域）的算法两大类（还有一类是彩色增强），如下图所示：

 

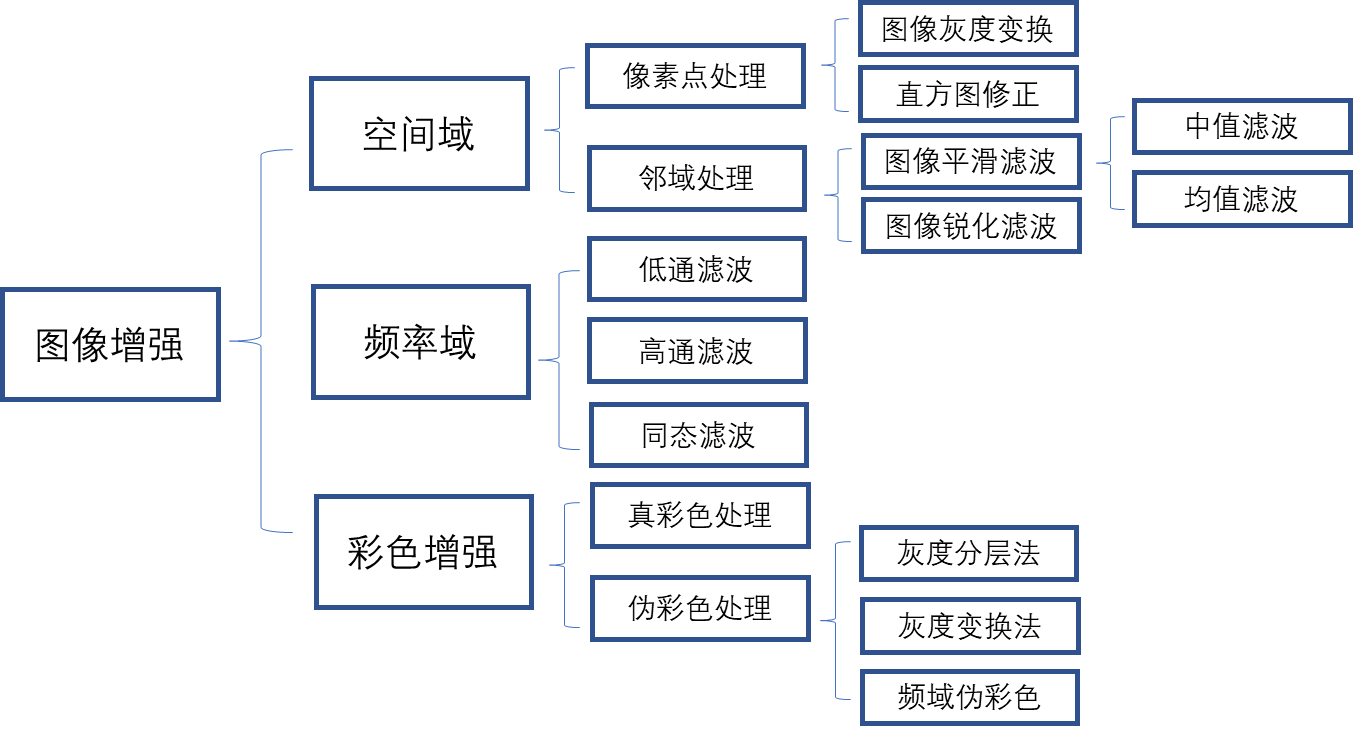
 1. 空间域图像增强算法

空间域图像增强算法直接对图像进行点运算或邻域处理。

点运算直接对像素灰度进行点对点映射，常见的点运算包括：灰度变换、直方图匹配（修正）和直方图均衡，以及某些图像的算数或逻辑运算等。图像的邻域增强则以某一像素为中心，综合该像素及其周围某一范围内（邻域）像素的灰度值进行计算，并将计算结果作为中心像素新的灰度值。

根据输出像素是否是输入像素及其邻域内像素的线性组合，可将图像邻域增强方法分为线性和非线性两大类。每一类方法又可分为低通滤波和高通滤波方法。低通滤波算法可以滤除图像中的高频噪声，使其变得更平滑；高通滤波则可以增强图像中目标的轮廓或边缘等高频细节，使其更锐化。

1.1、线性卷积

1.1.1、一维卷积

图像在空间域的增强常通过线性卷积运算来实现，它通过在图像中滑动一个模板，不断根据邻域像素的值计算各个像素的新值来完成计算过程。

根据信号处理理论，线性时不变系统可通过其传递函数来描述。如果忽略线性系统的内部细节，则线性系统在时域可抽象为输入信号f(t)与其传递函数冲击响应h(t)的卷积(Convolution)，在频域则可抽象为输入信号F(s)与其传递函数冲击响应h(s)的乘积。下图显示了基于传递函数的线性系统模型：

 

 

 卷积运算为积分运算，它反映了函数h(T)被反转为h (-T)后，沿r轴在另一个函数f(T)上移动时，与其所重叠部分乘积的积分。下图显示了两个函数进行卷积计算时的反转、平移及相乘和积分过程。

 

 

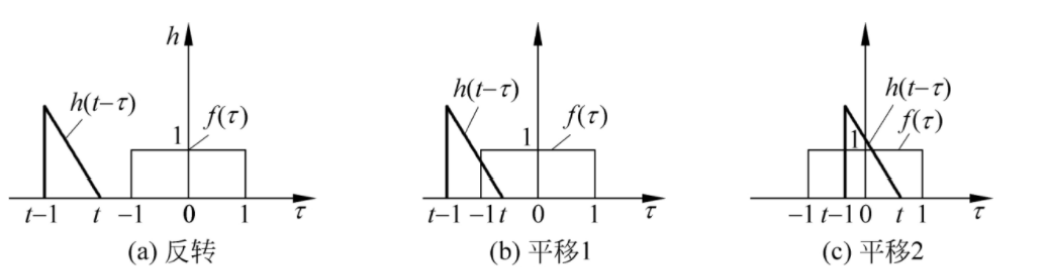
1.1.2、二维卷积

二维连续信号的卷积计算过程与一维卷积逻辑上类似。

计算时可以先将其中一个信号h(u，v)沿其原点旋转180°，然后以原点为中心沿u轴和v轴平移该信号（u轴平移x，v轴平移y）再将两个信号重叠部分相乘并积分，即得到原点处的输出。若信号为二维离散信号，则可以先将其中一个离散点阵序列h(m，n)沿其中心点旋转180°，然后以中心点沿另一离散点阵序列f(m,n)的横向和纵向滑动，每到一个位置，就把两个序列重叠的对应元素（中心点的邻域）相乘并且求和，即可得到该点的卷积。

若将离散二维信号f (m，n)看作是待处理的数字图像，并使h(m，n)点阵沿其中心对称（即旋转180°前后结果相同），就可以通过直接在数字图像f(m，n）中滑动h(m，n)完成图像的卷积运算。此时，被旋转180°后的h(-m，-n)点阵或沿中心对称的离散点阵h(m,n)被称为模板或卷积核（converlution kernel）。

图像卷积计算属于一种邻域处理方法。理论上来说，卷积核可以为任意尺寸，但是为了处理方便，它实际上常被设计为3×3、5×5或7×7等方形阵列。卷积核的类型决定了卷积运算对图像中的像素如何进行变换，卷积核中的元素值（权重）定义了它所覆盖的像素对中心像素的影响。在计算时，将卷积核由图像的左上角到右下角逐点平滑移动，每次滑动至一个新像素，都将卷积核中的每一因子作为权重值（绝对值越大，对中心点的影响越大），与它所覆盖的图像范围内的像素做加权求和，得到的结果作为它所覆盖的图像部分中心点的像素值。

下图显示了使用一个大小为3×3的卷积核对图像进行卷积运算时的过程。卷积核沿着图像左上角逐行、逐列滑动至右下角最后一个像素点。对于每次移动，卷积核中的9个元素P(x，y)都会和它覆盖的图像中对应的像素K(x，y)相乘并求和，得到的结果∑K (x, y)·P (x，y)将作为卷积核中心点在图像中所覆盖的像素P(x，y)的新值。当卷积核沿着所有像素滑动，并均完成前述计算后，图像的卷积计算即完成。

 

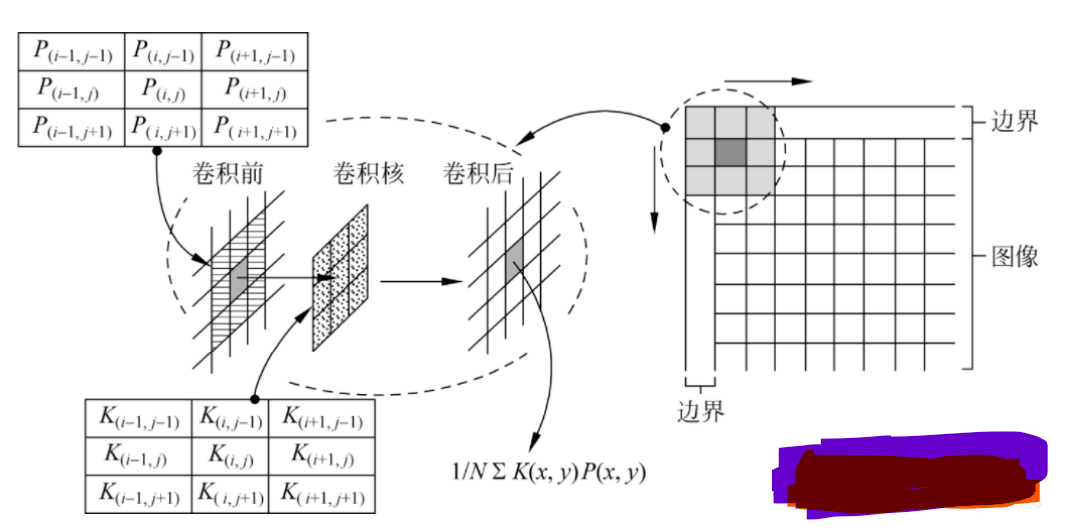
在机器视觉和图像处理系统开发过程中，卷积运算常用于对图像在空间域进行增强。具体是滤除图像中的噪声还是增强目标的轮廓或边缘等高频细节，由所选择的卷积核决定。

 

1.2、领域增强

图像的邻域增强，就是在空间域对其进行高通或低通滤波，以消除其中的噪声，锐化图像的轮廓，沿某一方向锐化目标的边缘等。

图像的空间域滤波直接根据像素及其周围邻域内的像素值，通过某种计算或变换得到新的像素值来实现滤波功能。如果输出像素是输入像素及其邻域像素的线性组合，则称为线性滤波，否则称为非线性滤波（中值滤波、边缘保持滤波等）。例如，基于卷积的图像邻域加权求和滤波就是一种空间域的线性滤波方法，而中值滤波等非加权计算形式的滤波则为非线性滤波。

一般来说，线性平滑滤波对去除各种噪声（如高斯噪声）较为有效。但是当信号频谱与噪声频谱混叠，或者当信号中含有非叠加性噪声时（如由系统非线性引起的噪声或非高斯噪声等），线性滤波在滤除噪声时，总会以某种方式模糊图像中的边缘和细节，进而降低图像中线性特征的可识别性。非线性滤波器常基于某种非线性映射关系，把某一特定的噪声近似地映射为零而保留信号的重要特征，因而其在一定程度上能克服线性滤波器的不足之处。

1.2.1、线性滤波

机器视觉系统开发过程中，常用的基于卷积计算的线性滤波方法有线性梯度算子（Linear Gradient）、拉普拉斯算子（Laplacian）、平滑滤波（Smoothing）和高斯算子（Gaussian）4种。其中，前两种方法用于锐化图像中灰度变化较快的高频边缘或纹理细节；后两种方法则用于滤除高频噪声和细节，使图像更平滑。下表对常用的线性滤波方法进行了汇总：

 

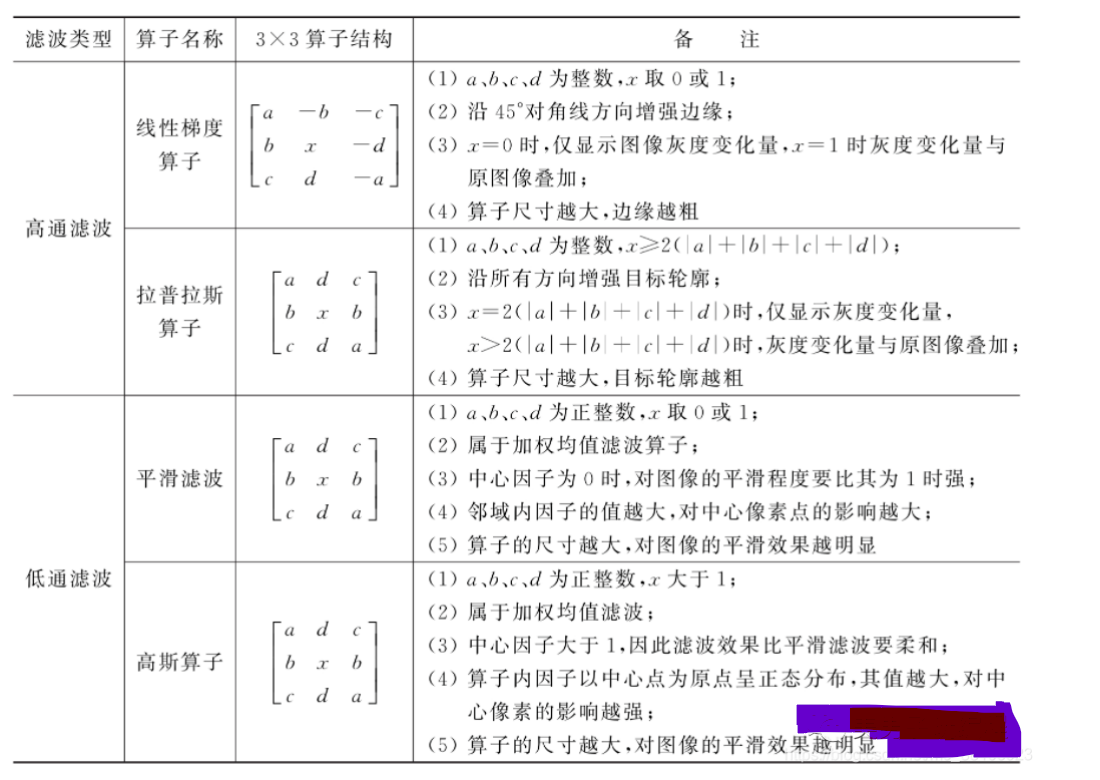
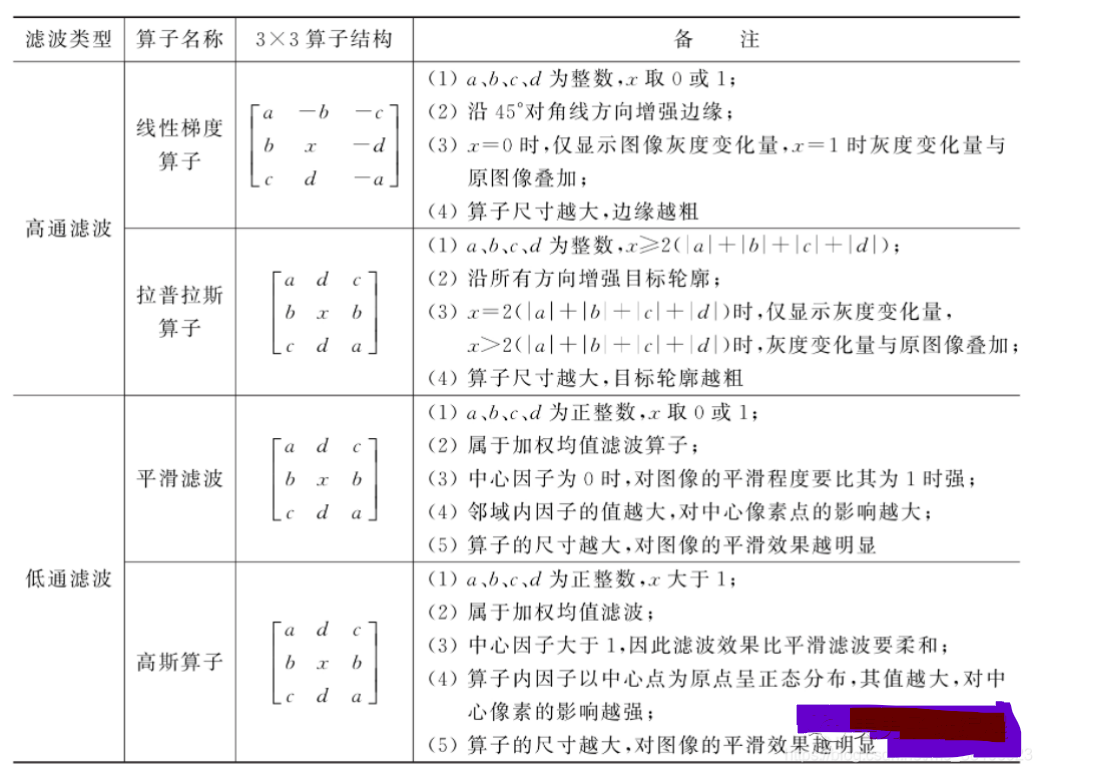
 邻域增强中的线性滤波多基于卷积运算，卷积核的尺寸限定了处理时的邻域大小，卷积核中的元素值设定了各邻域像素对中心像素影响的权重值，其绝对值越大，对中心像素的影响越大。如果卷积核中的因子有正有负，则滤波过程相当于邻域像素求权重差，其效果相当高通滤波；而如果卷积核中只有正因子，那么滤波过程相当相当于邻域像素求权重和，其效果相当低通滤波。线性梯度、Laplacian算子属于前一类，而高斯和平滑滤波属于后者。

1.2.2、非线性滤波

非线性滤波方法也可分为进行边缘检测的高通滤波和去除图像中杂散点的低通滤波两大类。

常用的非线性边缘检测（高通）方法有非线性梯度（Nonlinear Gradient）、Roberts、差值（Differentiation) 、Sobel、Prewitt、Sigma和Canny 7种。非线性低通滤波方法则有中值（Median）滤波、N阶滤波器、低通(Lowpass）滤波3种。下表对常用的非线性滤波方法进行了汇总：

 

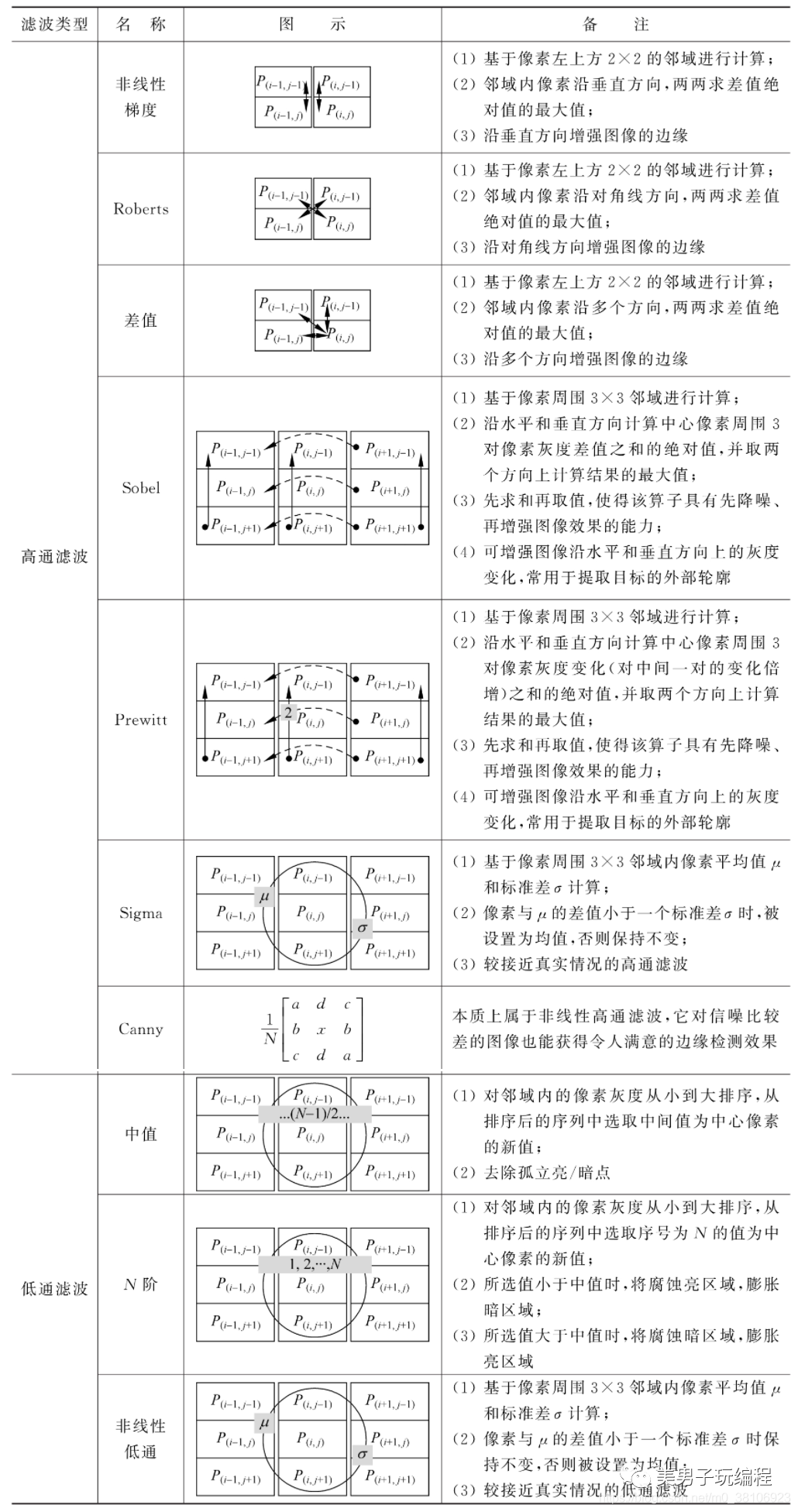
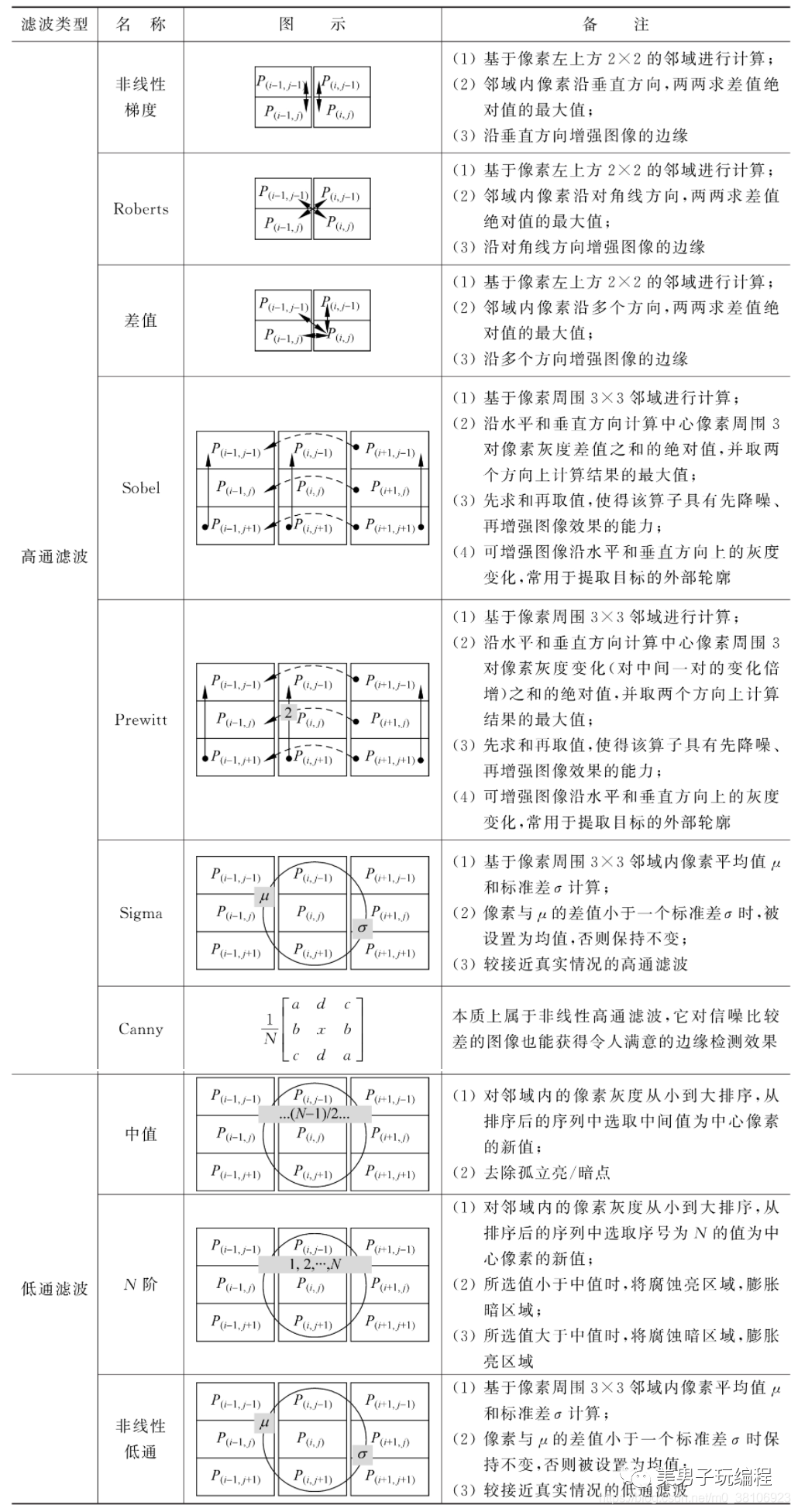
2.2、图像频域滤波

在图像处理中，图像的锐化与平滑处理可通过空间滤波或频域滤波来完成。从数学角度看，空间滤波是将信号与滤波算子进行卷积等运算的结果，具有方法直观、操作简便等优点。但当要处理的图像数据较大时，若没有发现比较高效的算法，就会有计算量大、计算时间长以及实时性差等缺点。

在频域对图像进行分析、增强时，不仅无须求解较难的微分方程，而且利用频谱图可直观地揭示系统性能，并可方便地选择有效抑制噪声的滤波器。此外，在频率域上进行图像处理时，还可以使用数字信号处理的一系列成熟方法和工具快速解决问题。

下面对常见的频域低通滤波器的特点进行了汇总和比较，可以看出：

• 理想低通滤波器处理的图像极为模糊，且含有很严重的振铃现象，但其对噪声的平滑效果好；

• 梯形低通滤波器的振铃现象不像理想滤波器那样严重；

• 巴特沃斯低通滤波器与指数低通滤波器相比，图像模糊程度低，但对噪声的平滑效果也差些；

• 高斯低通滤波器能在有效抑制噪声的情况下尽可能减小图像的模糊程度，因此它相对其他滤波器有较为广泛的应用。

比较下面所列出的几个高通滤波器可以发现：

• 理想高通滤波器处理的图像边缘抖动现象严重，且同时保留了边缘和噪声；

• 梯形高通滤波器会产生轻微抖动现象，但因计算简单经常被使用；

• 巴特沃斯滤波器锐化效果较好，边缘抖动不明显，但计算复杂；

• 指数高通滤波器比巴特沃斯滤波器效果差些，无边缘抖动现象；

• 高斯高通滤波器能在图像边缘抖动和锐化效果之间获得较好的平衡。