计算机视觉中的坐标系

分为像素坐标系、图像坐标系、相机坐标系、世界坐标系。

最终目标由世界坐标系转为像素坐标系。

1.    相机标定

【1】目的：求出相机的内、外参数，以及畸变参数。
【2】标定相机后通常是想做两件事：一个是由于每个镜头的畸变程度各不相同，通过相机标定可以校正这种镜头畸变矫正畸变，生成矫正后的图像；另一个是根据获得的图像重构三维场景。

• 内参数：镜头固有参数。such as, its focal length, skew, distortion, and image center. 镜头中心位置 (Cx，Cy) 和 焦距大小 fx，fy。均用像素长度表达。
• 外参数：摄像机位置参数，物体所处的现实世界坐标系对摄像机坐标系的刚性变换，可表达为旋转R 和 平移的结合 [R t]。

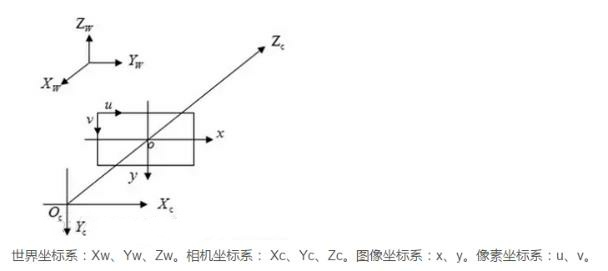
2.     世界坐标系到相机坐标的变换

设空间点Pw(Xw、Yw、Zw)，对应的相机坐标下坐标为Pc(Xc、Yc、Zc)：

1） 世界坐标系OwXwYwZw经旋转R、平移T得到相机坐标系OcXcYcZc

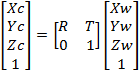                                              （1）

2） 成像平面坐标系(x,y)到图像坐标系(u,v)

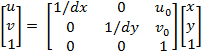                                 （2）

3） 相机坐标系OcXcYcZc到成像平面坐标系(x,y)，矩阵表示如下

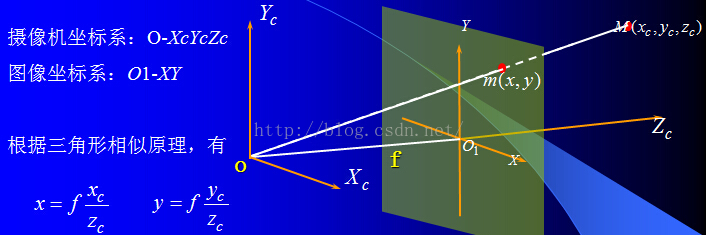
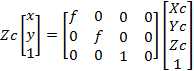                                  （3）

4） 因此，由上述(1)(2)(3)公式得到最终的转换过程，表示为：

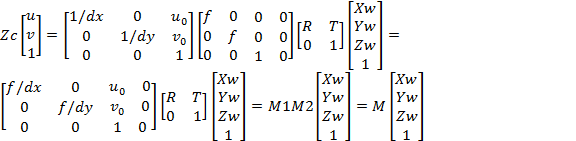_         （4）

由上式（4）可知M1与u0, v0, dx, dy, f等内参数有关，M2与R、T外参有关。

3.     相机畸变

相机的镜头会发生光学畸变，此时在成像坐标系下得到的坐标与真实坐标之间存在误差，镜头径向畸变解释如下：

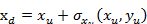                                              （5）

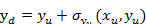                                              （6）

其中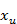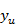（ , ）为理想状态下投影点的坐标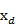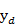，（ , ）为径向畸变引起的实际坐标值，k1，k2为径向畸变参数。为了使标定结果更加接近真实值，考虑用泰勒公式来计算径向畸变，则：

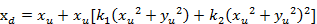          （7）

           （8）

参考链接：https://wenku.baidu.com/view/66f55b0702020740be1e9bd8.html