图论_迪杰斯特拉算法(Dijkstra)
Dijkstra算法
求解一系列点中任意两点间最短距离的算法 -- 图论最短距离
简介:
1. 案例:存在一系列的数据点(如9个点),我们将其编号为'A'~'I',这9个点的位置由坐标决定
在这11个顶点中,两两顶点之间或存在连线(即可通过其中一点直接达到另一点),
或不存在连线(即不可通过其中一点直接到达另一点), 现需要找到一条从0点到8点的最短距离的路径
2. 倘若存在一条路径(如'A' - 'B' - 'H' - 'I' - 'C' - 'F' - 'E')为最短路径
则存在以下定理:
该路径上任一点如'I'到起点'A'的距离也是起点到该点(或该点到终点)路径的最短距离。
证明:反证法
比如:路径中的7这个点, 'A' - 'B' - 'H' - 'I'这条路径一定是从 'A' 到 'I' 这个路径上最短的一条路径
如果不是(如 'A' 到 'I' 的最短路径为 'A' - 'C' - 'D' - 'I'),
则最初选择的从'A' 到 'E'的最短路径应为:'A' - 'C' - 'D' - 'I' - 'C' - 'F' - 'E'
得证
Dijkstra算法中存储信息的3个列表
1. 访问列表
记录该节点是否已经被访问过,未被访问为false,已被访问为true
visited = {
'A': false,
'B': false,
'C': false,
'D': false,
'E': false,
'F': false,
'G': false,
'H': false,
'I': false
}
2. 距离列表
用来记录从起点到每个节点的总距离信息,初始时,距离均为inf
距离列表可以用对象记录
dist = {
'A': inf,
'B': inf,
'C': inf,
'D': inf,
'E': inf,
'F': inf,
'G': inf,
'H': inf,
'I': inf
}
3. 父节点列表
用于存储每个被访问的节点的父节点是谁, 未被访问的节点父节点默认为-1
parent = {
'A': -1,
'B': -1,
'C': -1,
'D': -1,
'E': -1,
'F': -1,
'G': -1,
'H': -1,
'I': -1
}

function Dijkstra(Grapg, first, last){ // 1. 获取输入图结构的信息 // 1.1 获取节点列表 var vertexs = Grapg.vertexs; // 1.2 获取连线和权值信息 var edges = Grapg.Edges; /* 用于记录信息的三个列表: 访问状态列表 visited 距离列表 dist 父节点列表 parent */ // 2 列表初始化 var visited = {}; var dist = {}; var parent = {}; for(var i = 0; i < vertexs.length; i++){ visited[vertexs[i]] = false; dist[vertexs[i]] = Infinity; parent[vertexs[i]] = -1; } // 3 首次更新三个列表 visited[first] = true; dist[first] = 0; // 4. 依次访问节点,并在每次访问后更新三个列表,直到所有节点均被访问 var cur = first; while(Object.values(visited).some(item => item === false)){ /* 当还有节点未被访问时 */ // 4.1 更新dist表和parent表 // 获取当前节点cur的所连接的节点 var linkedVertex = Object.keys(edges[cur]); // 遍历这些节点,更新dist距离表和parent表 for(var k = 0; k < linkedVertex.length; k++){ // 只有未被访问过的节点才需要更新 if(visited[linkedVertex[k]] === false){ // 如果当前距离值小于起点直接到达该点距离值,则更新该点距离值 if(dist[cur] + edges[cur][linkedVertex[k]] < dist[linkedVertex[k]]){ // 更新dist距离表 dist[linkedVertex[k]] = dist[cur] + edges[cur][linkedVertex[k]]; // 更新parent表 parent[linkedVertex[k]] = cur; } } } // 4.2 更新visited表 // 找出未被访问的节点集合及对应的值 var uKeys = []; var uValues = []; for(var i = 0; i < vertexs.length; i++){ if(visited[vertexs[i]] === false){ // 数组ukeys中保存未被访问过的节点名 uKeys.push(vertexs[i]); // 数组uValues中保存未被访问过的节点到起点的距离 uValues.push(dist[vertexs[i]]); } } // 查找当前未被访问过的点的距离最小值 var minDist = Math.min(...uValues); // 查找当前未被访问过的点的距离最小值对应的那个节点名 var minVertex = uKeys[uValues.indexOf(minDist)]; // 更新当前点 cur = minVertex; visited[cur] = true; } // 4.4 根据parent表,总结出最佳路径 // 输出最佳路径 var path = [last]; while(path[0] != first){ var p = parent[path[0]]; path.unshift(p); } // 结果输出 var res = { visited, dist, parent, path }; return res; }
图结构封装:
// Graph_unDirected.js

// 1. 定义一个GraphData类,用来进行初始化数据添加 function Graph_unDirected(){ // 属性 // 1. 所有的节点存入到列表中 this.vertexs = []; // 2. 所有连线信息存入邻接表 this.Edges = {}; // 方法 // 1. 存入节点(每次存入一个) Graph_unDirected.prototype.addVertex = function(v){ if(this.vertexs.indexOf(v) == -1){ this.vertexs.push(v); this.Edges[v] = {}; }else{ alert("插入的节点为重复节点, 请检查!"); return false; } } // 2. 存入节点(每次存入多个) Graph_unDirected.prototype.addVertexs = function(v){ // 传入的数据v应为一个列表[...] for(var i = 0; i < v.length; i++){ // 若节点不存在,则插入 if(this.vertexs.indexOf(v[i]) == -1){ this.vertexs.push(v[i]); this.Edges[v[i]] = {}; }else{ alert("插入的节点 " + v[i] + " 为重复节点,请检查"); return false; } } } // 3. 存入距离信息(每次存入一条) Graph_unDirected.prototype.addEdge = function(v, v1, dist){ // 若原对象为空,则直接加入 if(!this.Edges[v]){ this.Edges[v] = {}; this.Edges[v1] = {}; this.Edges[v][v1] = dist; this.Edges[v1][v] = dist; } // 若该连线不存在,则添加 if(!this.Edges[v].hasOwnProperty(v1)){ this.Edges[v][v1] = dist; this.Edges[v1][v] = dist; console.log(this.Edges); }else{ alert("插入的连线为重复线, 请检查!"); return false; } return true; } // 4. 存入距离信息(每次存入多条) Graph_unDirected.prototype.addEdges = function(v, list){ // 这里输入的v为节点, list应为数组,数组元素为对象 // 如v = 8, list = {2: 2, 6: 6, 7: 1}, 表示节点8到节点2的距离为2,节点8到节点6的距离为6, 节点8到节点7的距离为1 // 取出邻接表中节点v对应的那个记录距离信息的对象, 如{2: 2, 6: 6, 7: 1} var [keys, values] = [Object.keys(list), Object.values(list)]; // 若v对应的距离列表为空 if(!this.Edges[v]){ for(var s = 0; s < keys.length; s++){ this.Edges[v][keys[s]] = values[s]; this.Edges[keys[s]][v] = values[s]; } return true; } // 若v对应的距离列表不为空 for(var i = 0; i < keys.length; i++){ var [kk, vv] = [keys[i], values[i]]; if(Object.keys(this.Edges[v]).indexOf(kk) == -1){ this.Edges[v][kk] = vv; if(!this.Edges[kk]){ this.Edges[kk] = {}; } this.Edges[kk][v] = vv; } } return true; } // 5. 打印邻接表 Graph_unDirected.prototype.toString = function(){ // 获取邻接表中所有的对象和值 var [ver, val] = [Object.keys(this.Edges), Object.values(this.Edges)]; var res = ""; for(var j = 0; j < ver.length; j++){ var [k1, v1] = [Object.keys(val[j]), Object.values(val[j])]; res += ver[j] + " --> "; for(var k = 0; k < k1.length; k++){ // 2: {1: 8, 3: 7, 8: 4, 8: 2}, res += k1[k] + ": " + v1[k] + " "; } res += "\n"; } return res; } }
案例测试:
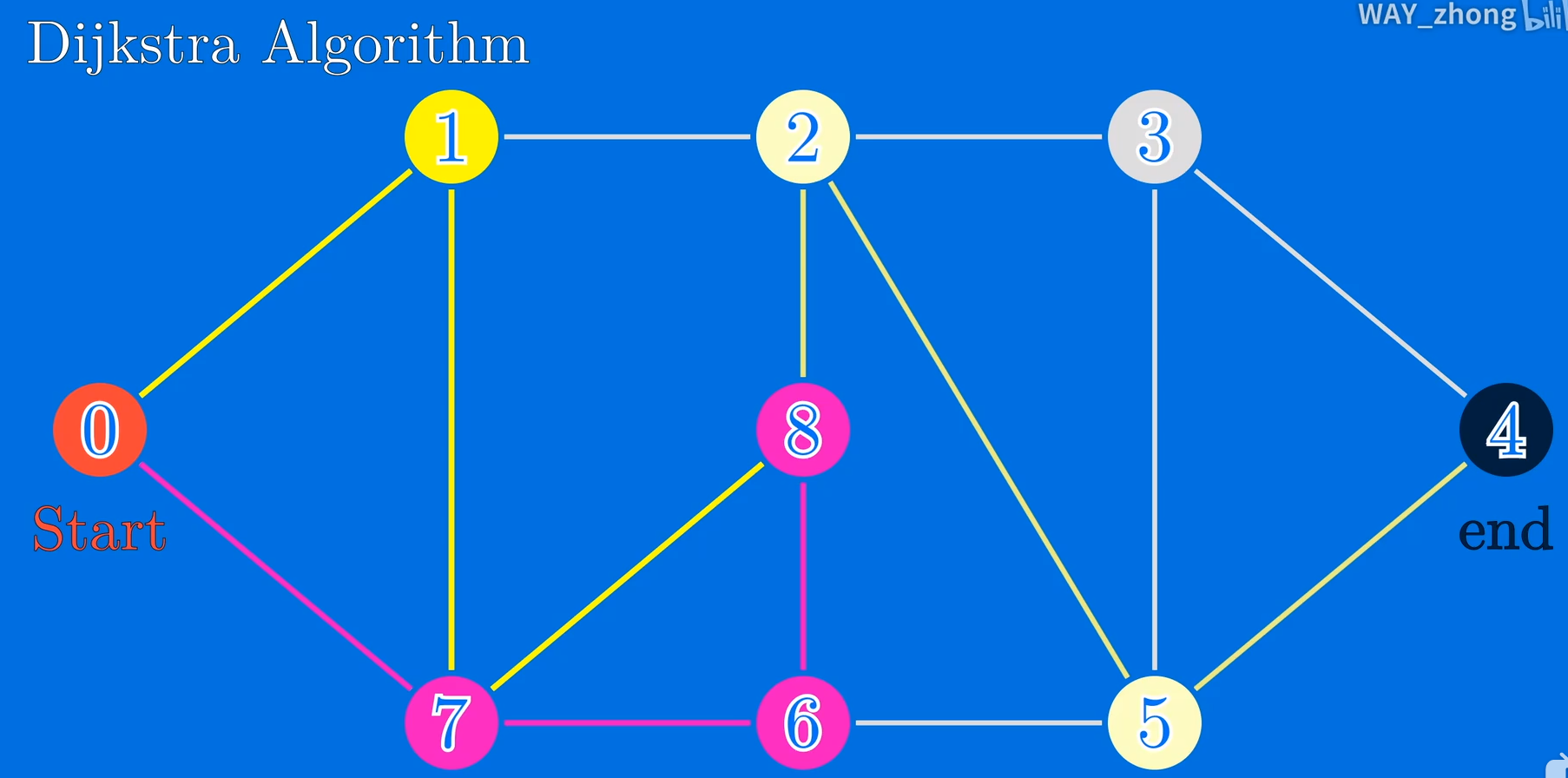
求解如图所示图结构中,从节点0到节点4的最短距离
// 测试代码

<script src="./Graph_unDirected.js"></script>
<script src="./Dijkstra.js"></script>
<script>
var g = new Graph_unDirected();
// 2. 添加节点
g.addVertexs(['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I']);
// 3. 添加连线和权值
g.addEdges('A', {'B': 4, 'H': 8});
g.addEdges('B', {'A': 4, 'C': 8, 'H': 3});
g.addEdges('C', {'B': 8, 'D': 7, 'F': 6, 'I': 2});
g.addEdges('D', {'C': 7, 'E': 9, 'F': 14});
g.addEdges('E', {'D': 9, 'F': 10});
g.addEdges('F', {'C': 6, 'D': 14, 'E': 10, 'G': 2});
g.addEdges('G', {'F': 2, 'H': 6, 'I': 6});
g.addEdges('H', {'A': 8, 'B': 3, 'G': 6, 'I': 1});
g.addEdges('I', {'C': 2, 'G': 6, 'H': 6});
// 4. 输出图内容
console.log(g.toString());
var res = Dijkstra(g, 'A', 'E');
console.log(res);
</script>




 浙公网安备 33010602011771号
浙公网安备 33010602011771号