K-means聚类算法

1. K-means聚类算法简介

　　采用的是将N*P的矩阵 X 划分为K个类，使得类内对象之间的距离最大,而类之间的距离最小。

2. 伪代码

输入：训练样本 x = {x₁;x₂;x₃;......x_m} (其中x为m-by-n矩阵，包含m个样本点，每个样本点n个特征)

　　　聚类簇数 k(为一标量scalar)

 

聚类过程：从x中随机选取k个样本顶啊作为初始聚类中心，k = {k₁,k₂,k₃,......k_k}.

　　　　　Repeat:

 

　　　　　　　　% （1）. 划分样本到特定的簇中

　　　　　　　　for j = 1,2,3,......n do　　　　

　　　　　　　　　　计算样本x_j与各聚类中心 k 的距离；

　　　　　　　　　　将该样本划进与其最近的样本中心 k_i 所在的簇中。

　　　　　　　　end for

 

　　　　　　　　% （2）. 更新聚类中心

　　　　　　　　for i = 1,2,3,......k do

　　　　　　　　　　计算新的聚类中心 k‘ = {k₁',k₂',k₃',......k_k'};

　　　　　　　　end for

　　　　　until 所有的聚类中心不再变化，或者说聚类结果不再变化

 

3. 优化目标

　　　　　

 

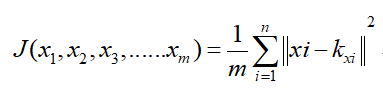
 4. 示例代码

 

% 输入 X 待聚类样本点，为 m - by - n 矩阵，包含m个样本点，每个样本点包含n个特征
% 输如 K 为用户自定义的所需划分的簇数，为一个标量

idx=Kmeans(X,K)
[idx,C]=Kmeans(X,K) 
[idx,C,sumD]=Kmeans(X,K) 
[idx,C,sumD,D]=Kmeans(X,K) 
[…]=Kmeans(…,’Param1’,Val1,’Param2’,Val2,…)

% 输出 idx 为 m - by - 1列向量，记录每个样本点所属的簇
% 输出 C 为 K - by - n 矩阵，记录最终各簇的聚类中心
% 输出 sumD 为K - by -1的和向量，存储的是类间所有点与该类质心点距离之和
% 输出 D 为 m - by - K 矩阵，存储每个样本点与各个聚类中心的距离


[…]=Kmeans(…,'Param1',Val1,'Param2',Val2,…)
这其中的参数Param1、Param2等，主要可以设置为如下：

1. ‘Distance’(距离测度)
‘sqEuclidean’ 欧式距离（默认时，采用此距离方式）
‘cityblock’ 绝度误差和，又称：L1
‘cosine’ 针对向量
‘correlation’  针对有时序关系的值
‘Hamming’ 只针对二进制数据

2. ‘Start’（初始质心位置选择方法）
‘sample’ 从X中随机选取K个质心点
‘uniform’ 根据X的分布范围均匀的随机生成K个质心
‘cluster’ 初始聚类阶段随机选择10%的X的子样本（此方法初始使用’sample’方法）
matrix 提供一K*P的矩阵，作为初始质心位置集合

3. ‘Replicates’（聚类重复次数）  整数