记录一次梯度爆炸+对比学习
背景
pytorch 训练tricks
对比学习,使用dropout构造正样本,出现对比学习loss越来越大最终nan。但是如果事先对向量进行l2正则化,loss正常下降。
解决过程
考虑有如下原因,一一排除并最终锁定:
- batch_size太大,导致分母过大,负样本过多,log里面的项无限接近于0,loss项过大(但是对比学习一般说负样本越多越好,基本排除batch_size太大)
- 向量维度过大,导致直接点乘的结果过大
- 温度系数过小(温度系数设为1后,依然爆炸,排除)
- dropout p=0.4设置的过大,导致正样本中含0元素过多,和负样本与正样本的乘积都差不多,很难优化。(设置p=0.1后,梯度爆炸现象消失,暂时解决)
分析
- 一般对比学习的话,l2 norm+tem是搭配使用的,如果不l2,直接点乘算相似度的话,比较popular的brand 会倾向于在一个batch内多次出现,即多次作为正例,模型希望这个向量本身和自身增强后的向量之间的相似度更大,模型会倾向于朝着增大这个向量模长的方向去学习,保证对于这个向量来说,他自己和自己的正样本的相似度是最大的。当这个brand作为其他emb的负样本时,其他emb为了和这个模长负样本emb点乘后拉开距离,他自己的emb也会模长更大,来保证自身正样本之间的dot product是最大的。如此以往,所有向量的模长都不断增大,便会容易出现nan,loss不断上升,的现象。
- 一般 l2norm+tem > dot product
- 对比学习的温度系数:当温度系数比较小,eg,0.07,模型其实关注的是最难的那一个样本;当温度系数比较大,模型区分不开,极端情况下的推导,n是和负样本的分数,p是和正样本的分数。
\[loss=-log\frac{e^{p/t}}{e^{p/t}+\sum e^{n/t}}=log\frac{e^{p/t}+\sum e^{n/t}}{e^{p/t}}=log(1+\sum e^{(n-p)/t})=log(1+e^{(n_1-p)/t}+e^{(n_2-p)/t}+...+e^{(n_x-p)/t})
\]
n有不同的难易程度,简单的负样本,n-p会比较小,甚至是负数,难的负样本,n-p会比较大,在用很小温度系数以后,括号内就会趋向于:
\[log(e^{(n_{max}-p)/t})=(n_{max}-p)/t
\]
模型的loss要想降低,就是在优化最难的负样本
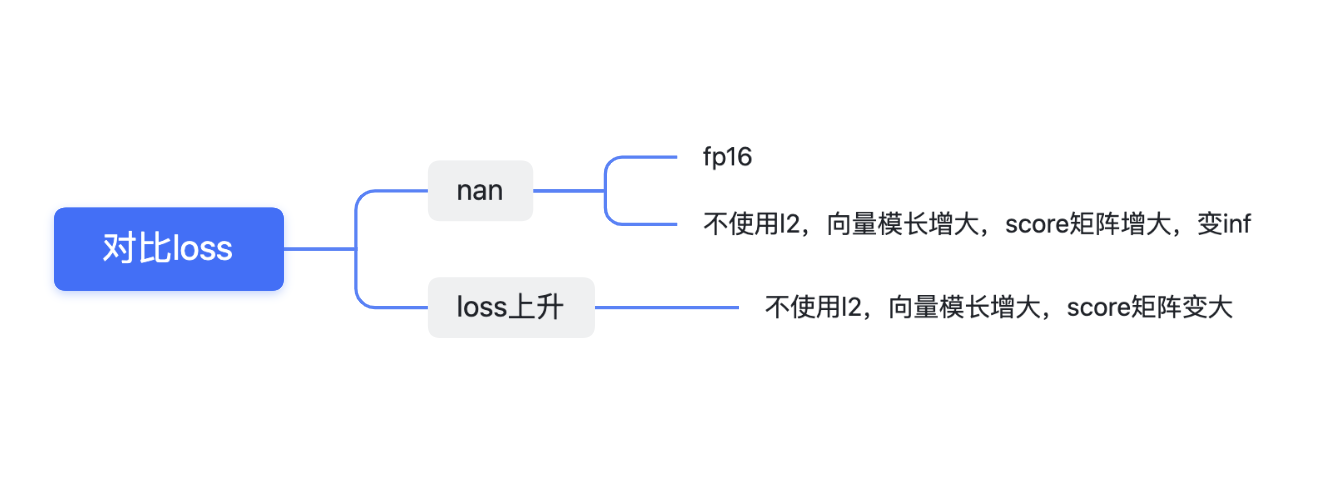
结论
- nan的来源:
- 根据上述分析可知,当不使用l2时,向量模长会倾向于越来越大,导致相似度矩阵的值也越来越大,在fp16的限制下,会变成inf。对inf求exp后,就得到了nan。
- 如果计算softmax之前,没有针对数值稳定性进行处理,会发生上溢/下溢的问题。Pytorch计算Loss值为Nan的一种情况【exp计算溢出,利用softmax计算的冗余性解决
- 而温度系数如果很小,eg,0.07,更加会放大相似度矩阵的值,导致更容易出现nan。(这也是为什么tem=1的时候,nan现象暂时消失)
- 解决方案:使用fp32 或者对emb向量进行l2norm
- loss不断上升
- 当不使用l2norm的时候,向量模长越来越大,向量之间相似度得分也会越来越大,根据公式,\((n-p)\)也会变大,所以loss会不断上升。
\[loss=log(1+e^{(n_1-p)/t}+e^{(n_2-p)/t}+...+e^{(n_x-p)/t})
\]
# 使用起来比较坑,他是从外而内的报错,如果报的error,我们自己打印发现没有问题,尝试简化代码,不断回溯。
with torch.autograd.detect_anomaly():
out = super(TevatronTrainer, self).training_step(*args) / self._dist_loss_scale_factor
记录score、模长,发现不断上升:
self.ttf_writer.add_scalar("scores", torch.mean(out.scores), self.state.global_step)
self.ttf_writer.add_scalar("doc_average_norm", torch.mean(torch.norm(out.p_reps, dim=1)), self.state.global_step)
self.ttf_writer.add_scalar("q_average_norm", torch.mean(torch.norm(out.q_reps, dim=1)), self.state.global_step)

