focal loss
- 动机：
- 1⃣️ 正负样本的比例可能十分不均衡，1:1000，且大部分负样本都是easy example
- 2⃣️ 虽然easy 样本（正类的分数接近1，负类分数接近0的那些）本身的loss就很低，但由于数量众多，依旧对loss有很大的贡献。
- 目标：用一个合适的函数去度量难分类样本和易分类样本对总损失的贡献
CE交叉熵损失函数：
\[L=-y_ilog(p_i)-(1-y_i)log(1-p_i)
\]
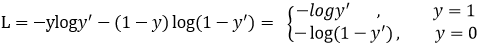
正样本损失函数变化，越接近于1，loss越接近于0；负样本损失函数，概率越接近0，loss越小
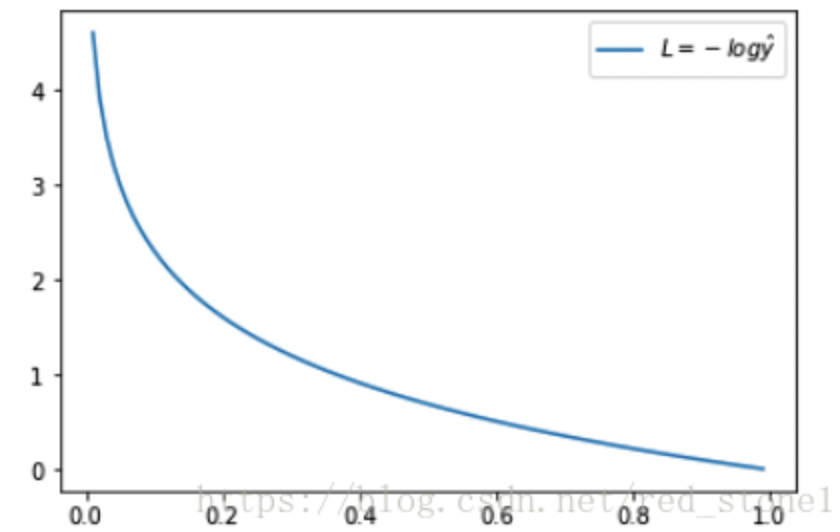
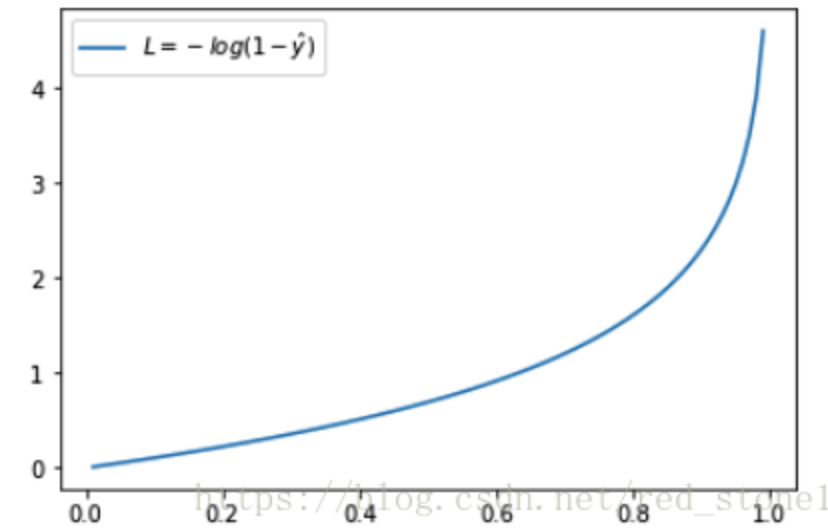
对于动机1⃣️，正负样本比例不平衡，通常会在交叉熵前面乘一个参数\(\alpha\)，可以理解如果正样本比例少，那我就多关注一些正样本的损失，alpha大一些。
对于动机2⃣️，虽然 \(\alpha\) 平衡了正负样本比例，但是对于难易样本的平衡没有任何帮助，虽然容易样本本身loss比较小，但是当其数量较多的时候还是会对整体的loss产生主导作用。于是，作者提出，乘以一个系数，把高置信度样本本身就就很小的loss再降的小一些。
举个例子，当 \(\gamma\) 为2的时候，对于一个容易的样本，比如p=0.968，其对应原本的loss是接近于0的，再乘以一个系数\((1-0.968)^2=0.001\) ，让原本就小的loss更小了，还衰减了1000倍！
最终focal loss对二者进行一个结合，来解决动机1和动机2进行综合
- 参数取值：
- 在gamma=0时，alpha=0.75效果更好，取值应该跟样本数量的倒数相关，
- 但当gamma=2时，alpha=0.25效果更好，个人的解释为负样本(IOU<=0.5)虽然远比正样本(IOU>0.5)要多，但大部分为IOU很小（如<0.1）就是负样本虽然很多但是都很简单容易，以至于在gamma作用后某种程度上贡献较大损失的负样本甚至比正样本还要少，所以alpha=0.25要反过来重新平衡负正样本。
- 也就是说，本来正样本难以“匹敌”负样本，但经过\((1-p_i)^{\gamma}\) 和 \(p_i^{\gamma}\) 的“操控”后，也许形势还逆转了，还要对正样本降权。
