数据结构知识点速览
数据结构知识点速览
1. 概论
1.1 大O记号
- 算法:正确性(可以解决指定问题)、确定性(任一算法都可以描述为一个由基本操作组成的序列)、可行性(每一基本操作都可以实现,且在常数时间内完成)、有穷性(对于任何输入,经有穷次基本操作,都可以得到输出)
- 好算法:正确 + 健壮 + 可读 + 效率(速度尽可能快,空间尽可能少。既要马儿快快跑,又要马儿吃的少)
- 大O记号:使用 TM模型-图灵机(Head累计移动次数)、RAM模型(random access machine,执行的基本操作次数)衡量算法效率,是一把尺子。而大 O 记号是尺子上的刻度,同时我们不追求精细的刻度。
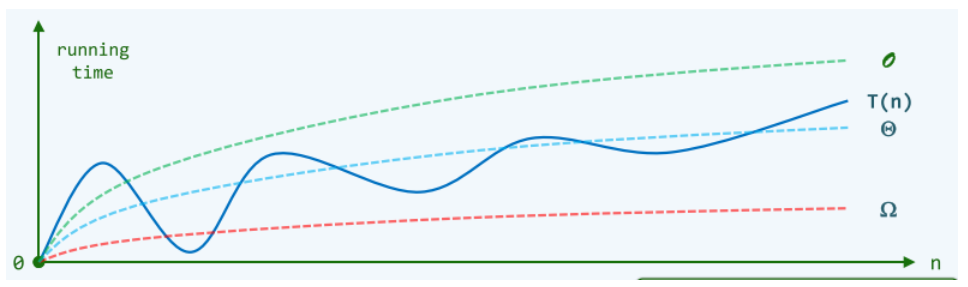
- 上界:\(T(n)=O(f(n)),if\) $ \exists {c>0},s.t.$ \(T(n) < c \cdot f(n)\) $ \forall n >> 2$
- 与 \(T(n)\) 相比,\(f(n)\) 在形式上更简洁,但依然可以反映前者的增长趋势!
- ① 常数项可忽略:\(O(f(n)) = O(c \cdot f(n))\)
- ② 低次项可忽略:\(O(n^a + n^b) = O(n^a),a \geq b >0\)
- 长远+主流:n足够大+常系数和低次项可忽略。
- 其他记号:
- 下界:\(T(n) = \Omega(f(n)),if\) \(\exists c > 0,s.t.T(n) > c \cdot f(n)\) \(\forall n >> 2\)
- 确界:$T(n)=\Theta(f(n)),if $ \(\exists c_1 > c_2 >0,s.t. c_2 \cdot f(n) < T(n) < c_1 \cdot f(n)\) \(\forall n >> 2\)
- 用的最多的还是大 O 记号
长远+主流!
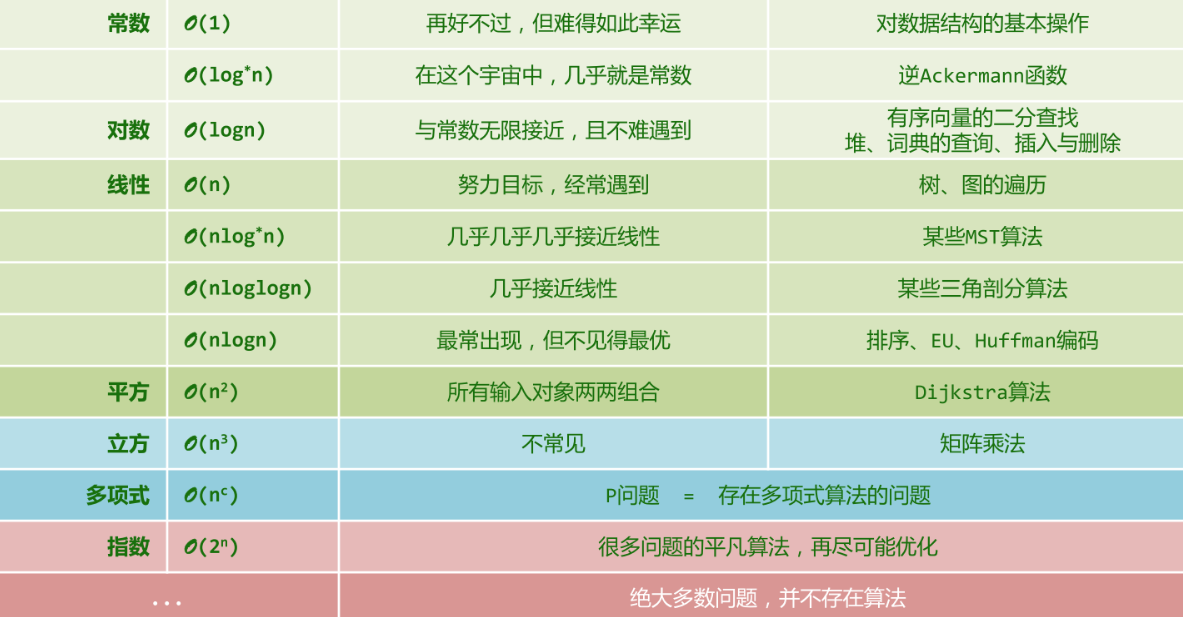
- 层次级别:(大 O 直尺上有哪些刻度)
-
刻度1:\(O(1)\),常数,效率最高
-
刻度2:\(O(log^cn)\),对数复杂度,此类算法非常有效,复杂度无限接近于常数。
- 常底数无所谓:\(\forall a,b >1,log_a n=\underline{log_ab \cdot log_bn} =\Theta(log_bn)\)
- 常数次幂无所谓:\(\forall c >0,logn^c = \underline{c \cdot logn} = \Theta(logn)\)
- 忽略低次项:\(123 \cdot log^{321}n+log^{205}(7n^2-15n+31)=\Theta(log^{321}n)\)
-
刻度3:\(O(n^c)\) ,多项式复杂度。
- 线性复杂度:\(O(n)\)
- 从 \(O(n)\) 到 \(O(n^2)\) 是本课程主要涵盖的范围。
-
刻度4:\(T(n) = O(a^n),a >1\) ,指数复杂度。eg,\(O(2^n)\),
- 这类算法的计算成倍增长极快,通常被认为不可忍受
- 从 \(O(n^c)\) 到 \(O(2^n)\) ,是从有效算法到无效算法的分水岭。
- eg:2-Subset 问题——S 中包含n个正整数,其和为 2m,问是否存在S的子集 T,满足 T中元素的和为 m ?直觉上,直接枚举 S 的每一个子集,并统计其中元素总和。子集个数为 \(|2^S|=2^{|S|}=2^n\) ,直觉算法需要迭代 \(2^n\) 轮,是否有更好的办法?定理:2-Subset 是NP-complete问题。即就目前的计算模型来说,不存在可在多项式时间内回答此问题的算法。
1.2 复杂度分析
- 复杂度分析的主要方法:
- 迭代问题:级数求和
- 递归问题:递归跟踪 + 递推方程
- 猜测 + 验证
- 相关级数:
- 算术级数:与末项平方同阶。\(T(n)=1+2+3+...+n=O(n^2)\)
- 幂方级数:比幂次高出一阶。\(\sum_{k=0}^nk^d=O(n^{d+1})\) (积分:\(\int_{0}^nx^ddx\))
- 几何级数:与末项同阶。\(T_a(n)=a^0+a^1+...+a^n=O(a^n),a>1\)
- 调和级数:\(h(n)=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{n}=O(logn)\)
- 对数级数:\(ln1+ln2+...+lnn=ln\prod_{i=1}^{n}k=lnn!=O(nlogn)\)
- 封底估算:
- 1天:\(10^5 s\)
- 1生:100yr,\(3×10^9 s\)
- 为祖国健康工作五十年:\(1.6 × 10^9 s\)
- 三生三世:300yr, \(10^{10} s\)
- 宇宙大爆炸至今:\(4×10^{17} > 10^8 × 一生\)
1.3 减而治之
- 减而治之:为求解一个大问题,可以
- ① 将其划分为两个子问题,其一平凡,另一规模缩减。
- ② 分别求解子问题
- ③ 由子问题的解,得到原问题的解
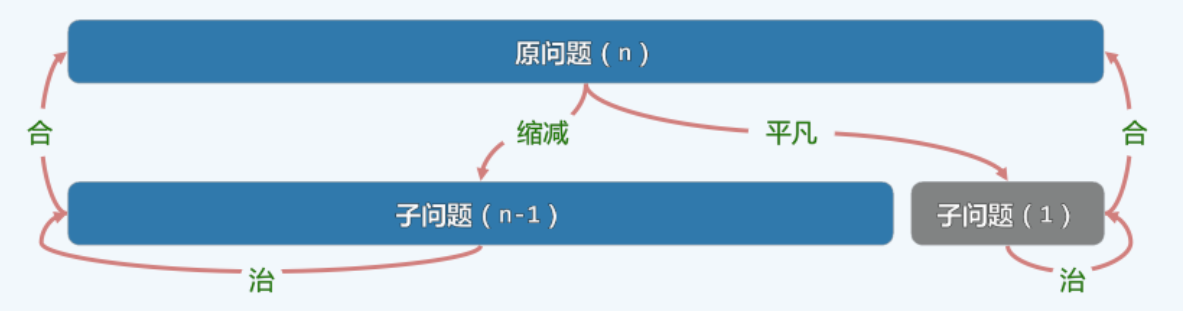
-
两种分析递归问题的复杂度的方法:
求解任意n个整数之和:

-
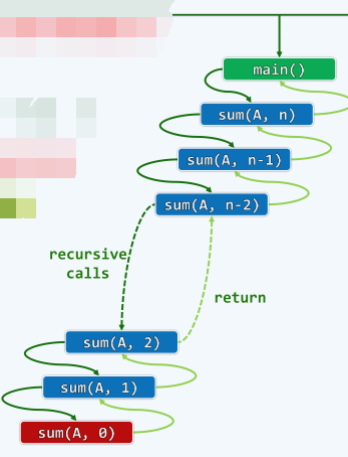
方法1-递归跟踪:
- 绘制出计算过程中出现过的所有递归实例(及其调用关系)
- 它们各自所需的时间之和,即为整体运行
- 本例中,共计 n+1 个递归实例,各自只需 O(1) 时间,故总体运行时间为:\(T(n) = O(1) × (n+1) = O(n)\)
-
方法2-递推方程:对于大规模问题、复杂的递归算法,递归跟踪不再适用。从递推的角度,
-
求解规模为 \(n\) 的问题 \(sum(A, n)\) 需要 \(T(n)\) 的时间
-
递归求解规模为 \(n-1\) 的问题 \(sum(A,n-1)\),需要 \(T(n-1)\)
-
再累加上 \(A[n - 1]\),需要 \(O(1)\)
-
**递推方程**:$T(n) = T(n-1)+O(1)$
**base 递归基**:$T(0)=O(1)$ $// sum(A,0)$
**求解**:$T(n)=T(n-2)+O(2)=T(n-3)+O(3)=...=T(0)+O(n)=O(n)$
1.4 分而治之
-
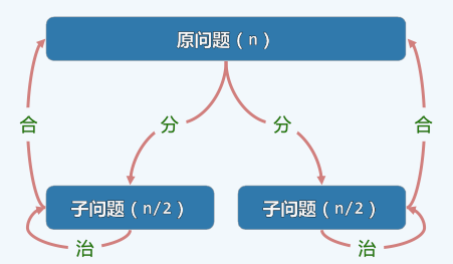
分而治之:为求解一个大规模问题,可以
- 将其划分为若干子问题(通常两个,且规模大体相当);
- 分别求解子问题;
- 由子问题的解合并得到原问题的解。
-
例:二分递归-数组求和,区间范围A[lo,hi)
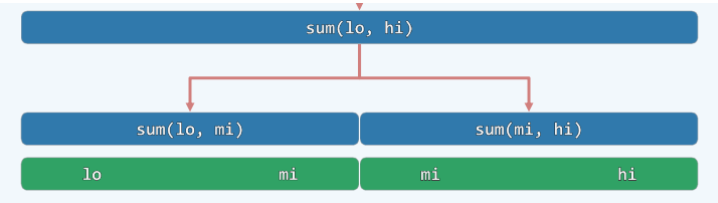

复杂度分析-递推方程:从递推的角度看,为求解 sum(A,lo,hi),需要
- ① 递归求解 sum(A,lo,mi) 和 sum(A,mi+1,hi) // 2*T(n/2)
- ② 进而将子问题的解累加 //O(1)
- 递推方程:\(T(n) = 2 \cdot T(n/2) + O(1)\)
- base 递归基:$T(1)=O(1) $
- 求解: \(T(n) = 4 \cdot T(n/4)+O(3) = 8 \cdot T(n/8)+O(7) = n \cdot T(1)+O(n-1)=O(2n-1)=O(n)\)
-
例:任给整数序列 A[0,n),找出其中总和最大的区段 // 有多个时,短者优先
版本1:蛮力算法 \(O(n^3)\),令 i 和 j 分别为区段的起点和终点,变量 k 遍历该区段统计总和

版本2:递增策略 \(O(n^2)\),固定 i ,随着 j 递增,每个区段的和可以在上一区段的基础上加上 \(A[j]\) 得到。
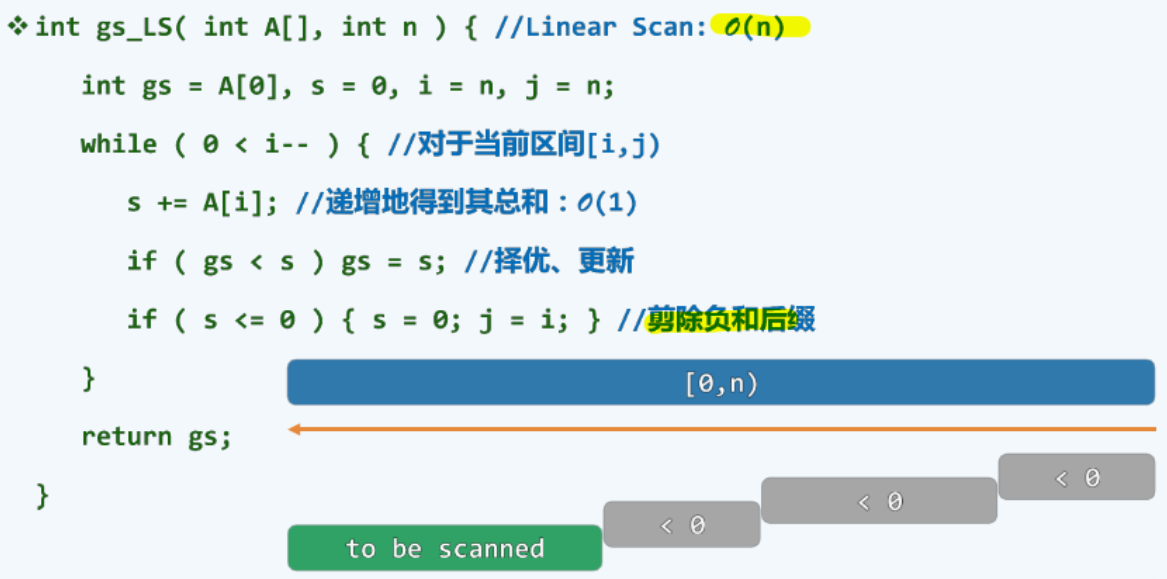
版本3:减治策略 \(O(n)\),剪除负和后缀,令 i 从后向前遍历,对遍历元素累加到 s,当s 大于全局最优 gs,就更新 gs;如果 s <=0,证明其没有贡献,剪除,s 重置为0,区间缩短,j = i;
1.5 动态规划与递归
-
动态规划 dynamic programming:自顶向下的递归,转换为自底向上的迭代
-
例:最长公共子序列 LCS longest common subsequence
- 子序列:由序列中若干字符,按原相对次序构成。
- 最长公共子序列 LCS:两个序列公共子序列中的最长者。(注意,可能有多个最长公共子序列,比如图左的DATA和DANA;也可能有歧义,比如下图右中我们的 D 可以取两个)
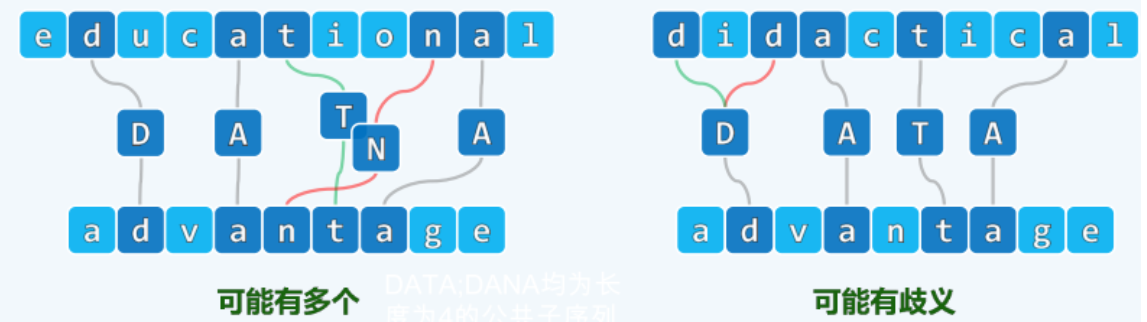
算法-递归:
对于子序列A[0,n] 和 B[0, m] ,LCS(n,m) 无非三种情况
0)递归基:若 n < 0 或 m < 0,则 LCS(n,m) 取做空序列 ("")
1)减而治之:若 A[n] == B[m],则 LCS(n,m) = LCS(n-1,m-1) + 1(末字符相等)
2)分而治之:若 A[n] != B[m],则在 LCS(n,m-1) 与 LCS(n-1,m) 中取较长者(末字符不相等)
对于递归策略,我们考虑其复杂度。我们发现:
- 最好情况,只需 O(n+m) 的时间,比如,一个序列是另一个的后缀时,不涉及分治。
- 最坏情况,因为一旦分治,不仅子问题数量增加,且可能大量雷同。据计算,特别当 n = m 时,复杂度为 \(\Omega(2^n)\)
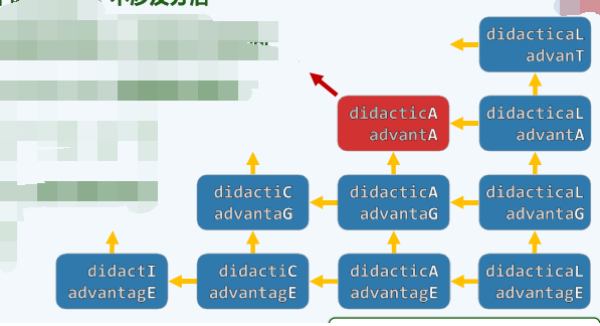
版本2:动态规划-迭代
与fib()相似,这里也存在大量重复的子问题(递归实例),各子问题,其实分别对应于 A 和 B 的某个前缀组合,实际上,总共不过 \(O(n \cdot m)\) ,采用动态规划的策略,便只需 \(O(n \cdot m)\) 时间即可计算出所有子问题,只需要
- 将所有子问题假想为一张表
- 颠倒计算方向,从 LCS(0,0) 出发,依次计算出所有项,直到 LCS(n,m)```
dp[i][j]的意思是字符串A中的[0,i]和B中的[0,j]中最长公共子序列的长度。
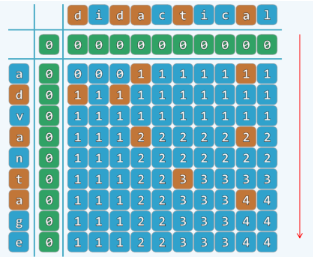
代码见leetcode 1143题。
2. 向量-循秩访问
向量 ADT 接口:【注,这里的接口和STL提供应该不太一样】
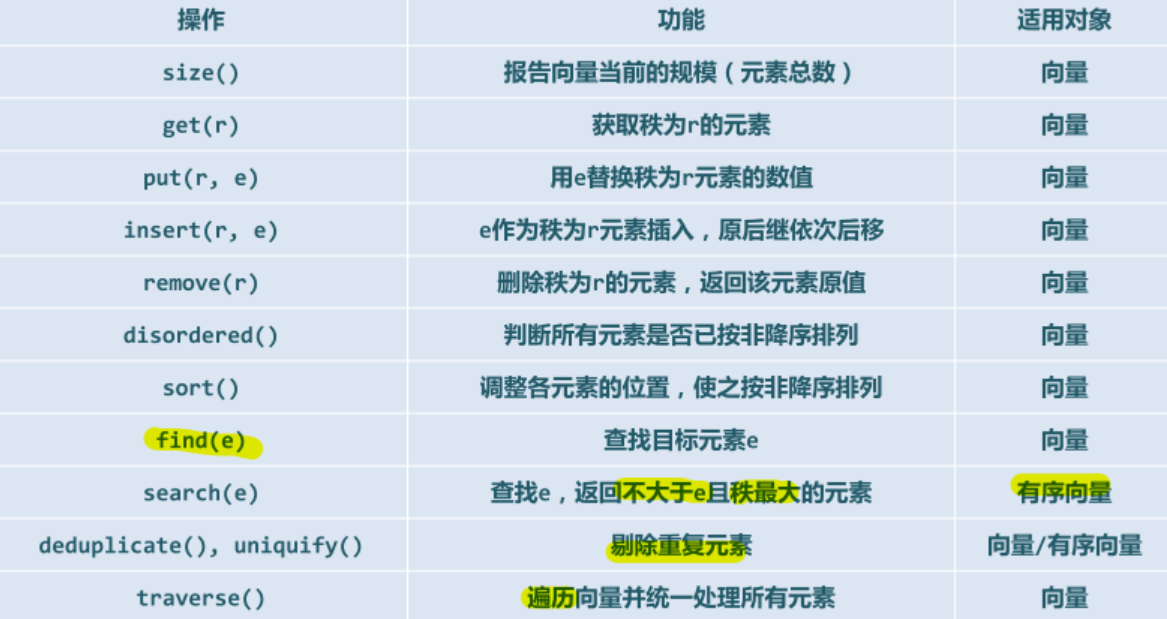
2.1 向量-模板类
template<typename T> class Vector{}
private 私有成员:
- 实际规模:Rank _size; // typedef int Rank; //秩
- 容量:int _capacity;
- 数据区:T* _elem
2.2 空间管理
- 上溢 overflow:_elem[]不足以存放所有元素。
- 下溢 underflow:_elem[]中的元素寥寥无几。
- 装填因子 load factor :\(\lambda = \_size/\_capacity << 50%\)
- 禅的哲学:身体经过一段时间生长,会褪去原来的外壳,代之以更大的新外壳。
- 倍增扩容算法:空间不足时扩容,原向量备份,_elem容量加倍,复制原向量内容,释放原空间。
- 递增扩容策略:每次扩容都是在原来的基础上追加一个固定的数额,而不是加倍对比二种策略,我们发现倍增策略明显优于递增扩容。
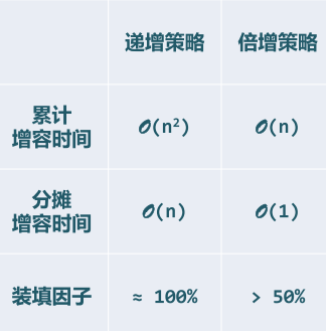
- 平均分析 vs 分摊分析
- 平均复杂度:根据数据结构各种操作出现概率的分布,将对应的成本加权平均。
- 将各种可能的操作,作为独立事件分别考虑
- 割裂了操作之间的相关性和连贯性,往往不能准确地评判数据结构和算法的真实性能。
- 分摊复杂度:对数据结构连续地实施足够多次操作,所需总体成本分摊至单次操作。
- 对一系列操作做整体考虑,更加忠实地刻画了可能出现的操作序列,更加精准地评判数据结构和算法的真实性能。
2.3 有序向量
-
有序/无序序列中,任何/总有一对相邻元素顺序/逆序。相邻逆序对的数目,可以在一定程度上度量向量的紊乱程度。
-
有序向量的去重:使用 Rank i 和 j 代表相邻互异“相邻”元素的秩。我们令j逐一扫描所有元素,和 i 所指元素比较,如果不等,则令 \(i++\) ,然后 \(\_elem[i]=\_elem[j]\) ;如果 j 所指元素和 i 所指元素相等,就令 \(j++\) 最后收缩区间,_size=++i,返回去重长度,\(j-i\)。
-
有序向量的二分查找:搜索区间均为左闭右开 [lo, hi)
- 对于无序向量的顺序查找: Rank find ( T const& e, Rank lo, Rank hi ):从后向前,顺序扫描查找,返回最后一个元素e的位置;失败时,返回lo - 1。
二分查找版本A:
- 在有序向量中,处处为轴点(说人话),以任一元素 \(S[mi]\) 为界,都可以将查找区间 \([lo,hi)\) 分为三部分,且 \(S[lo,mi) <= S[mo] <= S[mi,hi)\)
// 二分查找算法(版本A):在有序向量的区间[lo, hi)内查找元素e,0 <= lo <= hi <= _size
template <typename T> static Rank binSearch ( T* S, T const& e, Rank lo, Rank hi ) {
while ( lo < hi ) { //每步迭代可能要做两次比较判断,有三个分支
Rank mi = ( lo + hi ) >> 1; //以中点为轴点(区间宽度的折半,等效于宽度之数值表示的右移)
if ( e < S[mi] ) hi = mi; //深入前半段[lo, mi)继续查找
else if ( S[mi] < e ) lo = mi + 1; //深入后半段(mi, hi)继续查找
else return mi; //在mi处命中
} //成功查找可以提前终止
return -1; //查找失败
} //有多个命中元素时,不能保证返回秩最大者;查找失败时,简单地返回-1,而不能指示失败的位置
若轴点 mi 取做中点,则每经过至多两次比较,或者能够命中,或者将问题规模缩减一半。
复杂度-递推方程:\(T(n) = T(n/2) + O(1)=O(logn)\)
Fibonacci 查找算法:
- 动机:对于上述版本A,我们发现转向左、右分支前的关键码比较次数不等,而递归深度却相同(左分支搜索的比较次数小于右分支)。我们希望通过递归深度的不均衡,对转向成本的不均衡做补偿(多做成本低的),平均查找长度可以进一步缩短!
- 比如,若有 \(n = fib(k)-1\) (即向量长度 n 为某个斐波那契数-1),则可取 \(mi=fib(k-1)-1\) ,于是前、后子向量的长度分别为 \(fib(k-1)-1\),\(fib(k-2)-1\) 。
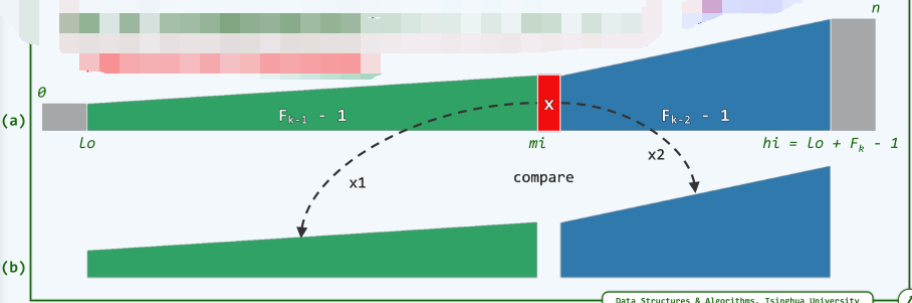
Fibonacci 查找的 ASL(平均成功查找长度) ,(在常系数的意义上)优于二分查找。
二分查找版本B:S[lo,hi) -> S[lo,mi) S[mi,hi)
对于 Fibonacci 查找,我们是试图使得整个搜索的倾向更偏向于成本低的左侧,使得向右的分支出现的概率更低,已经是最优的了。这里还有另一种改进思路:我们可以直接使得左右分支的成本相同。
- 每次迭代仅做一次关键码的比较,如此,所有分支只有2个方向,而不再是3个
- 同样,轴点 mi 取作中点,则查找每深入一层,问题规模也缩减一半
- e < S[mi]:则 e 若存在必然属于左侧子区间 S[lo,mi),故可递归深入。
- S[mi] <= e:则 e 若存在必然属于右侧区间 S[mi,hi),亦可递归深入。
// 二分查找算法(版本B):在有序向量的区间[lo, hi)内查找元素e,0 <= lo < hi <= _size
0010 template <typename T> static Rank binSearch ( T* S, T const& e, Rank lo, Rank hi ) {
0011 while ( 1 < hi - lo ) { //有效查找区间的宽度缩短至1时,算法才终止
0012 Rank mi = ( lo + hi ) >> 1; //以中点为轴点(区间宽度的折半,等效于宽度之数值表示的右移)
0013 ( e < S[mi] ) ? hi = mi : lo = mi; //经比较后确定深入[lo, mi)或[mi, hi)
0014 } //出口时hi = lo + 1,查找区间仅含一个元素A[lo]
0015 return e < S[lo] ? lo - 1 : lo; //返回位置,总是不超过e的最大者
0016 } //有多个命中元素时,不能保证返回秩最大者;查找失败时,简单地返回-1,而不能指示失败的位置
注:① 0011 行,原来是 \(hi - lo > 0\) ② 0015 行,原来是直接认定查找失败,这里还需要判断,如果最后剩下的一个元素,需要 \(S[lo]\) 和目标 \(e\) 比较,如果\(e < S[lo]\), 即最后剩下的元素比目标e大,就返回 \(lo-1\),否则证明查找成功,返回 \(lo\) 。
3. 排序 - 将无序向量转为更有优势的有序向量
使用c++ 自带函数 swap() 来进行交换的操作,使得代码的可读性和可移植性更好。swap 包含在命名空间 std 里面,不用担心交换变量精度的缺失,无需构造临时变量,不会增加空间复杂度。
3.1 起泡排序 bubbleSort
- 问题:给定 n 个可比较的元素,将它们按(非降)序排列。
- 观察:有序(无序)序列中,任何(总有)一对相邻元素顺序(逆序)。
- 扫描交换:依次比较每一对相邻元素;如有必要,交换之。若整趟扫描都没有进行交换,则排序完成;否则,再做一趟扫描交换。
- 相邻元素逆序:前者比后者大
提前终止版本:
void bubbleSort(vector<int>& nums, int lo, int hi){
// 起泡排序,交换
for(bool sorted = false; sorted = !sorted; ){
// 当sorted为true的时,取反为false退出
for(int i = lo; i < hi - 1; i++){
if(nums[i] > nums[i+1]){ // 逆序
swap(nums[i], nums[i+1]);
sorted = false;
}
}
}
}
正确性:
- 每趟扫描,我们都有一个无序部分的最大元素就位,因此,经过k趟扫描交换后,最大的k个元素必然就位。经过k趟扫描,问题规模缩减至 n-k,经过最多 n 趟扫描,算法必然终止,且能给出正确答案。
- 所以 n-1 趟扫描一定足够,但是往往不必,比如,[hi]就位后,[lo,hi)可能已经有序(sorted)——所以,我们只需要记录在当下扫描中是否做过交换,如果没有,则已经完全有序(没有相邻逆序对),提前停止。
- 对于 bubblesort 算法,交换次数恰好等于输入序列所含的逆序对总数。(那改进后的bubblesort,也输入敏感?是否也可以作为shellsort底层呢?)
复杂度:
- 时间效率: \(O(n^2)\)
- 空间复杂度:\(O(1)\)
- 稳定性:起泡排序是稳定的(重复元素在输入、输出序列中的相对次序保持不变),因为只有相邻元素才可以交换。
3.2 选择排序 selectionSort
动机:
假设我们有一篮子苹果,或大或小,需要从小到大排列,我们生活中会先选出最大的,再在剩下的中选择最大的…,其实之前的起泡排序BubbleSort也是一种选择排序,每次挑选出最大的往后交换。
但是起泡排序的效率太低,\(O(n^2)\) ,我们最大元素是小步慢跑式地一步一步交换到最后,是低效的来源。我们所以提出选择排序,一步到位。
扫描交换的实质效果无非是通过比较找到当前的最大元素M,并通过交换使之就位。如此看来,在经过O(n)次比较确定M之后,仅需一次交换即足矣。
void selectionSort(vector<int> & nums){
int n = nums.size();
for(int i = n-1; i >= 0; i--){ // 此轮的最大元素交换位置
int max_ = i;// 此轮最大元素的位置
for(int j = 0; j <= i; j++){ // 遍历前面无序部分
if(nums[j] > nums[max_]){
max_ = j;
}
}
swap(nums[max_], nums[i]);// 将选中的最大元素直接一次交换
}
}
性能分析:
- 共迭代n次,在第k次迭代中,选中最大元素为 \(\Theta(n-k)\),swap() 为 \(O(1)\),故总体复杂度应为 \(\Theta(n^2)\)
- 虽然如此,但是元素的移动操作远远少于起泡排序,这里的 \(\Theta(n^2)\) 主要来自元素的比较,成本相对更低。
- 但是,后面我们利用高级数据结构,可以把选出最大元素的操作在\(O(logn)\) 内完成,这样我们就可以得到 \(O(nlogn)\) 的排序算法。
- 时间复杂度:\(O(n^2)\)
- 空间复杂度:\(O(1)\)
- 稳定性:不稳定,因为随着我们每次把最大元素和对应位置元素交换,可能打乱原本的次序。
3.3 插入排序 insertionSort
动机:
我们之前的选择排序是苹果篮中取苹果,这里的插入排序我们可以想象,在打扑克牌时候的抓牌,我们每抓一张牌就将其插入到已经有序的牌中。
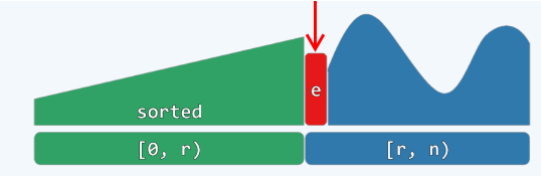
和选择排序的区别:
- 选择排序是后半部分有序,这里是左边有序
- 选择排序中我们不仅将序列划分为有序和无序两个部分,还要求无序前缀中任意一个值都不能超过有序后缀中的最小值,这里我们却没有类似的规定,无序部分大小任意(我们没抓到的牌也不知道大小)。
思路:
- 不变性:序列总能视作两部分 S[0,r) + U[r,n)
- 初始化,|S|=r=0
- 反复针对 e = A[r] 在 S 中查找适当位置,以插入 e。
每次都将当前元素插入到左侧已经排序的数组中,使得插入之后左侧数组依然有序。
对于数组 {3, 5, 2, 4, 1},它具有以下逆序:(3, 2), (3, 1), (5, 2), (5, 4), (5, 1), (2, 1), (4, 1),插入排序每次只能交换相邻元素,令逆序数量减少 1,因此插入排序需要交换的次数为逆序对数量。
void insertionSort(vector<int> nums){
int n = nums.size();
for(int i = 1; i < n; i++){
// 如果前面的元素比nums[i]大就一直先前交换
for(int j = i; j >= 1 && nums[j-1] > nums[j]; j--){
swap(nums[j-1],nums[j]);
}
}
}
性能分析:
- 插入排序属于就地算法,具有输入敏感性,因为后面可以看到shellsort之列的算法的高效性,完全依赖于insertionsort的这一特性。
- 最好情况:几乎完全有序,每次迭代只需1次比较,0次交换,累计 \(O(n)\) 时间。
- 最坏情况:几乎完全逆序,第 k 次迭代,需要 \(O(k)\) 次比较,1次交换,累计 \(O(n^2)\) 时间!
复杂度:
- 时间复杂度:\(O(n) — O(n^2)\)
- 空间复杂度:\(O(1)\)
- 稳定性:稳定,因为相邻元素如果相等是不会交换的。
- 备注:时间复杂度和初始顺序有关。
3.4 归并排序 mergeSort
我们知道bubbleSort 起泡排序的复杂度最坏情况 \(O(n^2)\) ,那么是否存在最坏情况下也可以做到 \(O(nlogn)\) 的排序算法。
原理:分治策略,向量与列表通用,整体运行成本应为\(O(n \cdot logn)\) (\(T(n)=2T(n/2)+O(n)\))
- 序列分为二,\(O(1)\)
- 子序列递归排序,\(2×T(n/2)\)
- 合并有序子序列,\(O(n)\)
0009 template <typename T> //向量归并排序
0010 void Vector<T>::mergeSort ( Rank lo, Rank hi ) { //0 <= lo < hi <= size
0011 if ( hi - lo < 2 ) return; //单元素区间自然有序,否则...
0012 int mi = ( lo + hi ) / 2; //以中点为界
0013 mergeSort ( lo, mi ); mergeSort ( mi, hi ); //分别排序
0014 merge ( lo, mi, hi ); //归并
0015 }
二路归并:有序序列,合二为一,\(S[lo,hi)=S[lo,mi)+S[mi,hi)\)
- 初始:j = 0,k = 0,j + k = 0
- 最终:j = lb,k = lc,j + k = lb + lc = hi - lo = n
- 每经过一次迭代,j和k至少会有一个加1,故知:merge() 总体迭代不超过 \(O(n)\) 次,累计只需线性时间!
template <typename T> //有序向量(区间)的归并
void Vector<T>::merge ( Rank lo, Rank mi, Rank hi ) { //各自有序的子向量[lo, mi)和[mi, hi)
T* A = _elem + lo; //合并后的向量A[0, hi - lo) = _elem[lo, hi)
int lb = mi - lo; // 前子向量的长度
T* B = new T[lb]; //前子向量B[0, lb) = _elem[lo, mi)
for ( Rank i = 0; i < lb; i++ )
B[i] = A[i]; //复制前子向量到B中
int lc = hi - mi; // 后子向量的长度
T* C = _elem + mi; //后子向量C[0, lc) = _elem[mi, hi)
// 前子向量合并完即可结束,若后子序列没有合并完依然会在对应的位置
for ( Rank i = 0, j = 0, k = 0; j < lb; ){ //归并:反复从B和C首元素中取出更小者
if(lc <= k || B[j] <= C[k]){
A[i++] = B[j++]; // 先进行这一步,保证稳定性
}else {
A[i++] = C[k++];
}
}
delete [] B; //释放临时空间B
}
归并排序复杂度分析:
- 时间复杂度: \(O(nlogn)\)
- 空间复杂度:\(O(n)\)
- 稳定性:只要实现恰当,可保证稳定性
缺点
- 非就地,需要对等规模的辅助空间
- 即便输入完全(或接近)有序,仍需要 \(O(nlogn)\) 时间
3.5 堆排序 heapSort
3.6 快速排序 quickSort
3.7 希尔排序 shellSort
4. 列表-和向量对称互补
4.1 静态到动态
操作方式:根据是否修改数据结构,所有的操作大致分为两类方式
- 静态操作:仅读取,数据结构的内容及组成一般不变:get、search
- 动态操作:需写入,数据结构的局部或整体将改变:insert、remove
数据元素的存储与组织方式:与操作方式相对应,也分为两种
- 静态:① 数据空间整体创建或销毁; ② 数据元素的物理存储次序与其逻辑次序严格一致;③ 可支持高效的静态操作 eg:向量
- 动态:① 为各数据元素动态地分配和回收物理空间 ② 相邻元素记录彼此的物理地址,在逻辑上形成一个整体 ③ 可支持高效的动态操作 eg:列表
4.2 列表(逻辑排列,物理不是)-循位置访问
- 列表(list)是采用动态存储策略的典型结构,其中的元素称为节点(node),通过指针或引用彼此联接;在逻辑上构成一个线性序列:\(L={a_0,a_1,...,a_{n-1}}\)
- 前驱后继:相邻节点彼此互称前驱(predecessor)或后继(successor)。
- 首末节点:没有前驱的节点称作首节点(first/front),没有后继的节点称作末节点(last/rear)。
- 从秩到位置:向量支持循秩访问(call-by-rank),根据元素的秩,可在O(1)时间内直接确定其物理地址;然而对于列表循秩访问的成本过高,应改用循位置访问(call-by-position),即利用节点之间的相互引用,找到特定节点。
4.3 节点类
typedef int Rank; //秩
#define ListNodePosi(T) ListNode<T>* //列表节点位置
template <typename T> struct ListNode { //列表节点模板类(以双向链表形式实现)
// 成员
T data; //数值
ListNodePosi(T) pred; //前驱
ListNodePosi(T) succ; //后继
// 构造函数
ListNode() {} //针对header和trailer的构造
ListNode ( T e, ListNodePosi(T) p = NULL, ListNodePosi(T) s = NULL ): data ( e ), pred ( p ), succ ( s ) {} //默认构造器
// 操作接口
ListNodePosi(T) insertAsPred ( T const& e ); //紧靠当前节点之前插入新节点,返回新节点位置
ListNodePosi(T) insertAsSucc ( T const& e ); //紧随当前节点之后插入新节点,返回新节点位置
};
4.4 List类
template <typename T> class List { //列表模板类
private:
int _size; //规模
ListNodePosi(T) header; //头哨兵
ListNodePosi(T) trailer; //尾哨兵
protected:
/*内部函数*/
public:
/*析构函数、析构函数、可读接口、可写接口、遍历接口*/

头、首、末、尾节点的秩可分别理解为 -1、n-1、n
得益于哨兵(头、尾节点),我们无需对首末节点做特殊处理!
列表-ADT接口【实现时画图,理清关系!】

- ListNodePosi(T) find ( T const& e, int n, ListNodePosi(T) p ) ;:find(e,n,p) —— 在p的n个前驱中查找 e 。
- find(e,p,n)——在p的n个后继中查找 e。
- ListNodePosi(T) find ( T const& e );:return find ( e, _size, trailer ); 从尾节点到前面查找所有。
4.5 几个接口实现
- 无序列表去重 deduplicate():将列表分为三部分,已经去重+p+未去重
template <typename T> int List<T>::deduplicate() {
int oldSize = _size; // 记录原规模
ListNodePosi(T) p = first(); // return header->succ; 首节点
ListNodePosi(T) q = NULL;
//在p的r个前驱中查找p,如果存在,删除q(因为下一步是p->succ,为了安全,我们删除前面那个)
for ( Rank r = 0; p != trailer; p = p->succ, q = find ( p->data, r, p ) )
q ? remove ( q ): r++; //r为无重前缀的长度
return oldSize - _size; //即被删除元素总数
}
复杂度:find() 是 \(O(n)\),remove() 是\(O(1)\),一共 n 次for循环,总体 \(O(n^2)\)
- 有序向量的去重 uniquify():把相同的元素看作一个分组
template <typename T> int List<T>::uniquify() { //成批剔除重复元素,效率更高
if ( _size < 2 ) return 0; //平凡列表自然无重复
int oldSize = _size; //记录原规模
ListNodePosi(T) p = first(); ListNodePosi(T) q; //p为各区段起点,q为其后继
while ( trailer != ( q = p->succ ) ) //反复考查紧邻的节点对(p, q)
if ( p->data != q->data )
p = q; //若互异,则转向下一区段
else remove ( q ); //否则(雷同),删除后者
return oldSize - _size; //列表规模变化量,即被删除元素总数
}
复杂度:只需要遍历整个列表一遍,remove() 操作 \(O(1)\),总体只需 \(O(n)\)
- 值得一提的是,对于有序列表和无序列表的查找操作,思路都是最原始的查找,无法借助有序性提高查找效率。和有序向量的二分查找不同,因为按照循位置访问的方式,物理存储地址与其逻辑次序无关。依据秩的随机访问无法高效实现,而只能依据元素间的引用顺序访问。
5. 栈
LIFO:last in first out 后进先出
栈是受限制的序列,只能在栈顶(top)插入和删除,栈底(bottom)为盲端
栈属于序列的特例,可以通过向量或列表派生(这里选择的是向量),向量末端作为栈顶,这样的 push、pop、top 均只需要\(O(1)\) 的时间。
5.1 基本接口
- s.size():返回栈中元素数目
- s.empty():栈空则返回真
- s.top():返回栈顶元素
- s.pop():出栈
- s.push(e):入栈
5.2 应用场合
栈的典型应用场合:
-
逆序输出:输出次序与处理过程颠倒;递归深度和输出长度不易预知,eg conversion 进制转换
-
递归嵌套:具有自相似性的问题可递归描述,但分支位置和嵌套深度不固定,eg stack permutation + parenthesis 栈混洗+括号匹配
-
延迟缓冲:线性扫描算法模式中,在预读足够长之后,方能确定可处理的前缀,eg evaluation
-
栈式计算:基于栈结构的特定计算模式,eg RPN
(1)逆序输出:进制转换
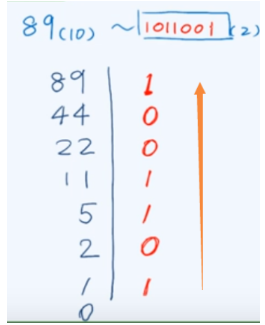
使用栈:计算过程中每得到一个数位就压入栈,后进先出,我们通过一系列pop操作,按压入的逆序得到我们需要的结果。
void convert ( Stack<char>& S, __int64 n, int base ) { //整数n的1<base<=16进制打印(迭代版)
char digit[] = "0123456789ABCDEF"; //数位符号,如有必要可相应扩充
while ( n > 0 ) { //由低到高,逐一计算出新进制下的各数位
S.push ( digit[ n % base ] ); //余数(当前位)入栈
n /= base; //n更新为其对base的除商
}
} //新进制下由高到低的各数位,自顶而下保存于栈S中
main(){
Stack<char> S; //用栈记录转换得到的各数位
convert ( S, n, base ); //进制转换
while ( !S.empty() )
printf ( "%c", ( S.pop() ) ); //逆序输出栈内数位,即正确结果
}
(2.1)递归嵌套:括号匹配
自相似性:某个局部和整体有相似性。
思路:
- 消去一对紧邻的左右括号,不影响全局的判断,用栈扫描,凡遇到左括号则进展,遇到右括号,则出栈。当遇到右括号,且栈为空时,代表不匹配。如果最后,栈中依然有左括号,也不匹配。
bool paren(const char exp[], int lo, int hi){
Stack<char> S; // 使用栈记录已发现但尚未匹配的左括号
for(int i = lo; i < hi; i++){ // 逐一检查当前字符
if('(' == exp[i]) S.push(exp[i]);//遇到左括号,进栈
else if (!S.empty()) S.pop();// 遇到右括号,栈非空,弹左括号
else return false; // 遇右括号,栈已空,必不匹配
}
return S.empty(); // 如果最终栈空,才代表匹配
}
- 上述思路也可推广至多括号并存的情况,eg \([ ( ] )\) ,我们只要遇到左括号(无论是大中小),都入栈;然后遇到右括号,将对应的栈顶左括号弹出即可,如果此时栈顶并非对应的左括号,代表不匹配。如果最终,栈中有剩余的左括号,也不匹配。
(2.2)递归嵌套:栈混洗问题 stack permutation
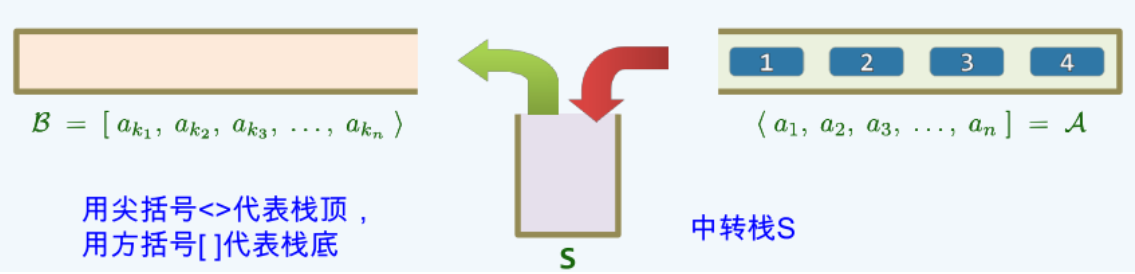
用尖括号<>代表栈顶,用方括号[ ]代表栈底
-
混洗:考察栈 \(A=<a_1,a_2,a_3,...,a_n],B=S=∅\) ,只允许将 A 的顶元素弹出并压入S,或将 S 的栈顶元素弹出并压入B,经一系列操作后,A 中元素全部转入 B 中,此时 ,\(B=<a_{k1},a_{k2},a_{k3},...,a_{kn}]\) 称为 A 的一个栈混洗 (stack permutation)。
-
问题:给出输入序列 \(<1,2,3,...,n]\) 的任一排列 \([p_1,p_2,p_3,...,p_n>\) 是否为栈混洗?
-
计数:\(SP(1)=1\) ,\(SP(n)=catalan(n)=\frac{(2n)!}{(n+1)! \cdot n!}\) n个数的序列的栈混洗数量。
-
思路:
-
简单的情况:\(<1,2,3],n=3\)
-
栈混洗共 \(\frac{6!}{4! \cdot 3!}=5\) 种
-
全排列共 \(3!=6\) 种
-
发现少了一种,是\([3,1,2>\) ,记住这个顺序,算法核心。
-
观察:任意三个元素能否按照相对次序出现在混洗中,与其他元素无关。
-
因此,对于任何 \(1<= i < j < k <= n\)(秩),\([...,k,...,i,...,j,...>\) 必定不是栈混洗。
-
-
定理:一个序列是栈混洗,当且仅当其不包含序列 321。
-
甄别算法:
- \(O(n^3)\) :对于\((i,j,k)\) 依次遍历,看看是否有 312 出现?
- \(O(n^2)\) :\([p_1,p_2,p_3,...,p_n>\) 是 \(<1,2,3,...,n]\) 的栈混洗,当且仅当,对于任意 \(i < j\) ,不含模式 \([...,j+1,...,i,...,j,...>\) ,如此可得到一个 \(O(n^2)\) 的甄别算法。
- \(O(n)\):直接借助栈 A、B 和 S 模拟混洗过程,每次 S.pop() 之前,如果栈 S 为空或者需要弹出的元素在S中非栈顶,立即判断栈混洗是非法的。
(3)延迟缓冲:中缀表达式求值 evaluation
-
减而治之:优先级高的局部执行计算,并被代之以其数值;运算符渐少,直至得到最终结果。
-
自左向右扫描表达式,用栈记录已扫描的部分(含已执行运算的结果)。在每一字符处:
while(/*栈顶存在可优先计算的子表达式*/) /*该子表达式退栈;计算其数值;计算结果进栈*/ /*当前字符进栈,转入下一字符*/// 主算法 float evaluate(char* S, char* & RPN){ Stack<float> opnd; // 运算数栈 Stack<char> optr; // 运算栈 optr.push('\0'); // 铺垫 while(! optr.empty() ){ // 逐个处理各字符,直至运算符栈空 if(isdigit(*S)){ // 若为操作数(可能多位、小数),读入 readNumber(S, opnd); }else { // 若为运算符,则视其与栈顶运算符之间优先级的高低 switch(orderBetween( optr.top(), *S)) { case '<': // 栈顶运算符优先级更低 optr.push(*S); // 运算符入栈 S++; break; case '=': // 优先级相等,当前运算符为右括号或尾部哨兵'\0' optr.pop(); // 脱括号,接收下一字符 S++; break; case '>': char op = optr.pop();// 栈顶运算符出栈 if( '!' == op ) // 一元运算符 opnd.push(calcu(op, opnd.pop())); else{ float pOpnd2 = opnd.pop(); float pOpnd1 = opnd.pop(); opnd.push(calcu(pOpnd1,op,pOpnd2)); } break; } } // while return opnd.pop(); // 弹出最后的计算结果 }- \('<'\) :静待时机
- \('>'\) :时机已到
- \('='\) :终须了断
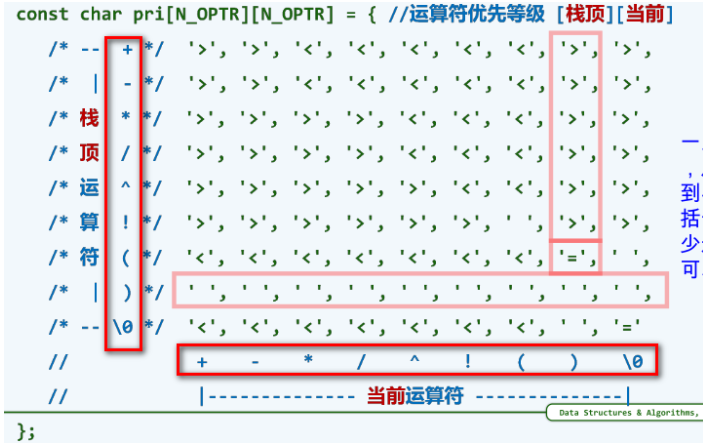
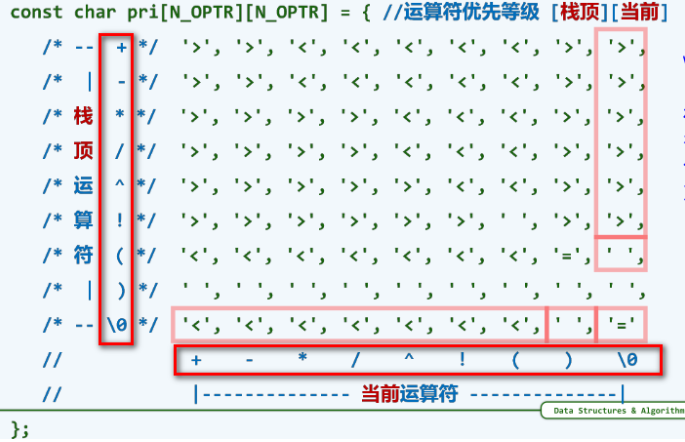
优先级表:
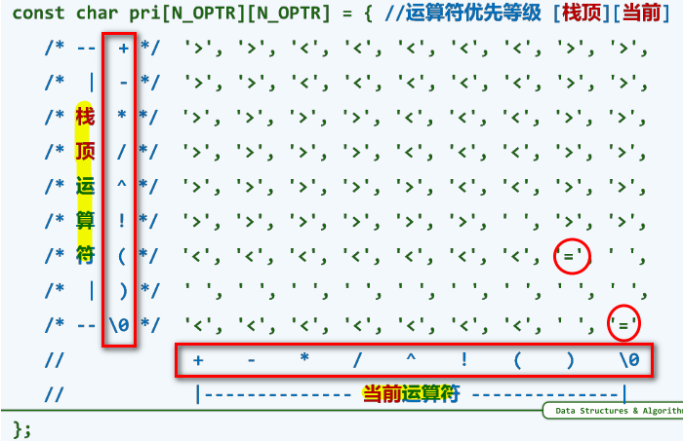
优先级表记忆方法:
- \(+\) \(-\) \(*\) \(/\) \(!\) :芸芸众生
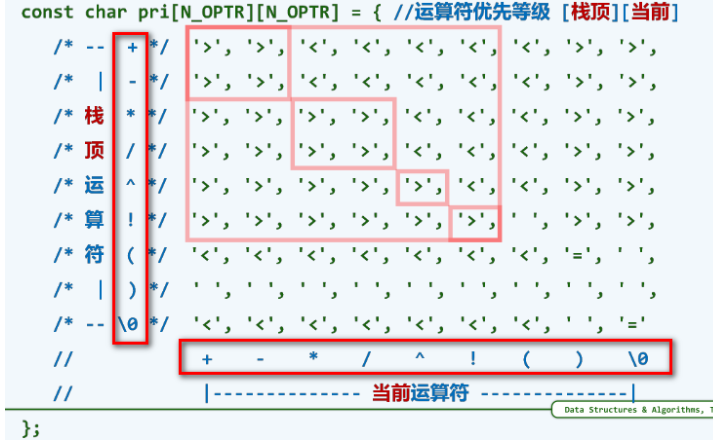
-
\((\) :我不下地狱,谁下地狱— 如果栈顶运算符是左括号,可以接纳任何运算符入栈;作为回报,当左括号作为当前运算符时,无论谁是栈顶,也会接纳它入栈。
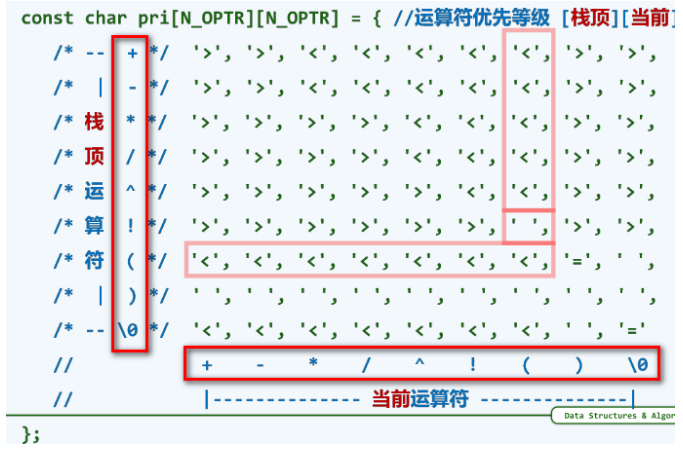
-
\()\) :死线已至,然后满血复活。一旦右括号作为当前运算符,从这个右括号到与其匹配的左括号间无论多少运算符都到了可以计算的时机。
-
\('\0'\) :从创世纪,到世界末日。当\('\0'\) 作为栈顶运算符时会谦逊的迎接任何运算符入栈;当其作为当前符号时,会促成其他栈中任何运算符的执行。
(4)栈式计算:RPN reverse Polish Notation 逆波兰表达式
两个栈,数字栈和符号栈
-
后缀表达式计算
- 1、如果是数字,那么直接入栈到num中
- 2、如果是运算符,将栈顶的两个数字出栈(因为我们考虑的运算符加、减、乘、除都是双目运算符,只需要两个操作数),出栈后对两个数字进行相应的运算,并将运算结果入栈
- 3、直到遇到'\0'
-
中缀表达式转后缀表达式
- 1、从左往右扫描中缀表达式 ,以1*(2+3)为例。s
- 2、如果是数字那么将其直接入栈到num中
- 3、如果是操作数,需要进一步判断
- (1)如果是左括号'('直接入栈到opera中
- (2)如果是运算符('+'、'-'、'*'、'/'),先判断数组opera的栈顶的操作数的优先级(如果是空栈那么直接入栈到数组opera),如果是左括号那么直接入栈到数组opera中,如果栈顶是运算符,且栈顶运算符的优先级大于该运算符,那么将栈顶的运算符出栈,并入栈到数组num中,重复步骤3,如果栈顶运算符优先级小于该运算符,那么直接将该运算符入栈到opera中。
- (3)如果是右括号')',那么说明在opera数组中一定有一个左括号与之对应(在你没输错的情况下),那么将opera中的运算符依次出栈,并入栈到num中,直到遇到左括号'('(注意左括号不用入栈到num)。
- 4、如果中缀表达式扫描完了,那么将opera中的操作数依次出栈,并入栈到num中就可以了,如果没有没有扫描完重复1-3步
其实和我们之前的中缀表达式求值一样,我们在对中缀表达式求值的同时可以完成 RPN 的生成。
// 主算法 float evaluate(char* S, char* & RPN){ Stack<float> opnd; // 运算数栈 Stack<char> optr; // 运算栈 optr.push('\0'); // 铺垫 while(! optr.empty() ){ // 逐个处理各字符,直至运算符栈空 if(isdigit(*S)){ // 若为操作数(可能多位、小数),读入 readNumber(S, opnd); /*!!!!!!!!!!!!!!!!!!1*/ append(RPN, opnd.top()); // 接入 RPN }else { // 若为运算符,则视其与栈顶运算符之间优先级的高低 switch(orderBetween( optr.top(), *S)) { case '<': // 栈顶运算符优先级更低 optr.push(*S); // 运算符入栈 S++; break; case '=': // 优先级相等,当前运算符为右括号或尾部哨兵'\0' optr.pop(); // 脱括号,接收下一字符 S++; break; case '>': char op = optr.pop();// 栈顶运算符出栈 /*!!!!!!!!!!!!!!!!!!1*/ append(RPN, op); // 接入 RPN if( '!' == op ) // 一元运算符 opnd.push(calcu(op, opnd.pop())); else{ float pOpnd2 = opnd.pop(); float pOpnd1 = opnd.pop(); opnd.push(calcu(pOpnd1,op,pOpnd2)); } break; } } // while return opnd.pop(); // 弹出最后的计算结果 }对RPN的引用和修改只出现在两个位置:①操作数接入RPN尾部②当前字符是运算符,只在其作为栈顶可以立即执行时,接入RPN。
-
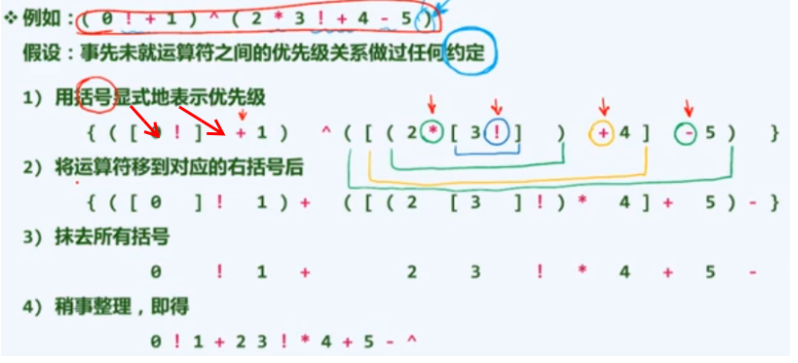
手动中缀转后缀
6. 队列
- 队列 (queue)也是受限的序列,只能在队尾插入,只能在队头删除,先进先出 FIFO。
- 队列也属于特殊的序列,也可以基于向量或列表派生,这里选择的是基于列表List派生,将列表首作为队列头,列表末作为队列尾。如此实现的入队、出队、队首操作均只需 \(O(1)\) 时间。
6.1 队列应用
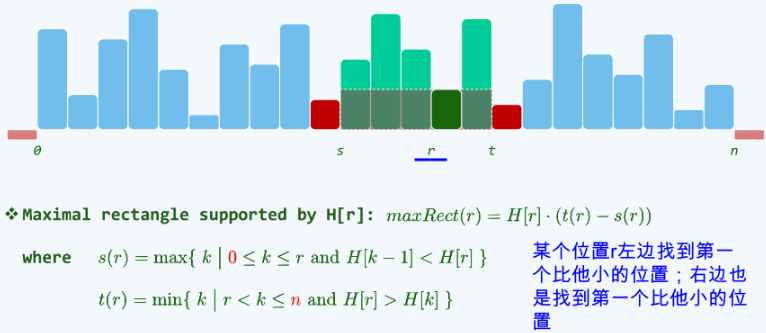
直方图内最大矩形,分别求出包含每个柱子的矩形区域的最大面积。

-
蛮力搜索:对于每个位置 r,都需要遍历找到 \(s(r)\) 和 \(t(r)\) ,需要 \(O(n^2)\) 的时间。
-
栈:\(O(n)\) 一趟线性扫描可以得到所有的 \(s(r)\) 。遍历每个柱子,然后分下边几种情况。
- 1.如果当前栈空,或者当前柱子大于栈顶柱子的高度,就将当前柱子的下标入栈 。
- 2.当前柱子的高度小于栈顶柱子的高度。那么就把栈顶柱子出栈,当做当前要求面积的必须包含的柱子。
- 3.而右边第一个小于当前柱子的下标就是当前在遍历的柱子,左边第一个小于当前柱子的下标就是当前新的栈顶(原栈顶在栈中的前一个元素,就 是左边第一个小于它的,因为原栈顶只有大于它才能被压栈)。
class Solution { public: int largestRectangleArea(vector<int>& heights) { // 求包含每个柱子的最大高度 // 对每一个i,高度就是heights[i],宽度是左右两边比它小的第一个柱子之间的距离 int n = heights.size(); if(n == 0){ return 0; } stack<int> sta; int maxarea = INT_MIN; for(int i=0;i<n;i++){ if(sta.empty()){ sta.push(i); continue; } int front = sta.top();// 栈顶下标 if(heights[i] >= heights[front]){ sta.push(i); }else{ // 把所有比heights[i]大的heights[sta.top()]都去计算面积 while(!sta.empty() && heights[i] < heights[sta.top()]){ front = sta.top(); // 完整包含front柱子的区域大小 int height = heights[front]; // 必须包含的柱子高度 sta.pop(); int left; if(sta.empty()){ left = -1; }else{ left = sta.top(); } // 正在遍历的元素就是右边第一个小于heights[栈顶]的下标 int right = i; if(maxarea < height * (right-left-1)){ maxarea = height * (right-left-1); } } sta.push(i); } } while(!sta.empty()){ // 栈里还有元素,就是一直到最后都没有出现比栈顶小的元素了 int front = sta.top(); sta.pop(); int left; if(sta.empty()){ left = -1; }else{ left = sta.top(); } int right = n; // 一直到末尾也没有小于剩下数中最大的栈顶的,自然也没有小于剩下所有数的 if(maxarea < heights[front]* (right-left-1)){ maxarea = heights[front]* (right-left-1); } } return maxarea; } };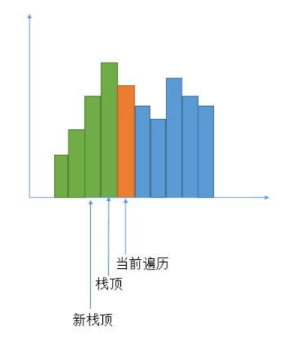
7. 树
动机:
- 为什么要提出树呢?vector和list不够用了吗?
- 综合性:List 和 Vector 均无法兼顾静态和动态,我们Tree就是将二者的优点结合起来,兼顾高效的查找、插入、删除。
- 半线性:树不再是简单的线性结构,但在确定了某种次序后,具有线性特征。为了和非线性图结构区别,我们称其为半线性结构。