软件工程网络15结对编程作业1（201521123034陈凯欣）

一、结对编程

• 陈凯欣：学号 201521123034+邱晓娴：学号 201521123037
• 码云地址：https://gitee.com/carolfantasy/software_engineering__pair_programming.git

二、需求分析

1、原项目分析

1.1项目类图

)

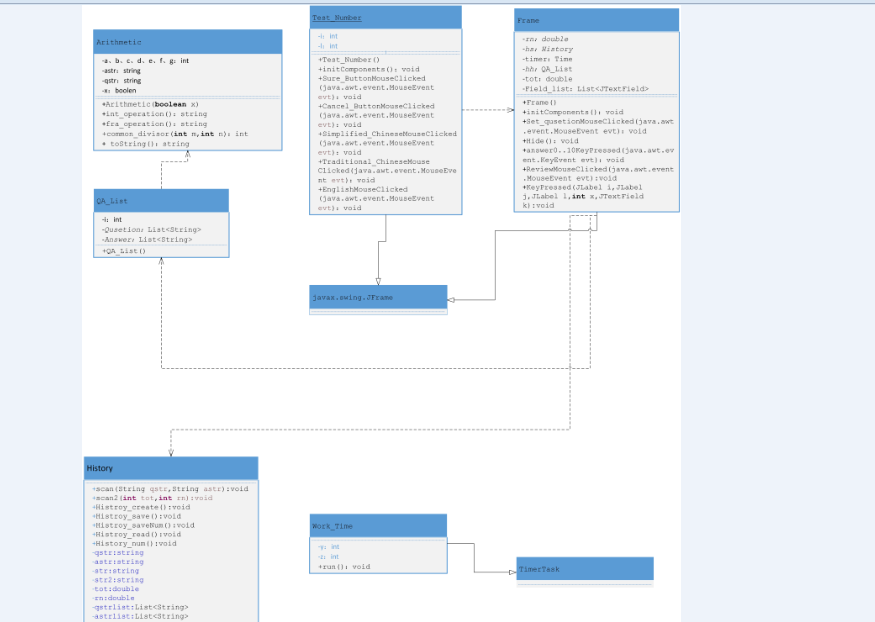
1.2逻辑泥球

• 做题界面除了开始的按钮以外只有一个复习按钮。这个程序的初衷是做题，那么复习这个选项应该是可选的，而不是必选。

)

• 变量的命名使用abc，不够规范。a既然表示操作符可以改名为oprator。

)

• 程序的不足之处：

• 运行该程序，初次选择计算题数并进行计算，程序会将错题存在错题集中。之后所有的计算练习是在错题集中抽取。需要重新运行该程序才能选择新的题目进行练习。（在做题页面增添一个功能——选题）

• 复习错题选择的题数若超过错题集题数，未提示错误。（添加提示）

• 题目的结构都为两个数和单操作符构成。（设计生成多操作符计算题，且一次随机生成的题目中，不允许有多个通过运算规则化简后结果相同的式子）

• 计时器显示的时间使用 框架，在做题界面中点击开始后修改计时时间，计时器停止运行，最后做题显示时间为手动修改的时间。（将显示时间的框架修改为不可人为输入的 框架）

• 在做题界面点击开始后，再次点击开始，计时器重新计时，导致做题时间不准确。（首次点击开始后，再次点击开始不触发任何事件）

• 错题集的题目根据每次做题的情况依次累加。若某题错误率高，随机选题复习的话很有可能选的题目都是该题，显得累赘。（在错题后添加一个变量——记录错题算对减去算错的次数。错题的次数为0时，从错题集中删除。按照次数由高到低选择错题进行复习。）

1.3原项目测试用例

（到位或不到位）

• 原项目测试用例
  
  
  

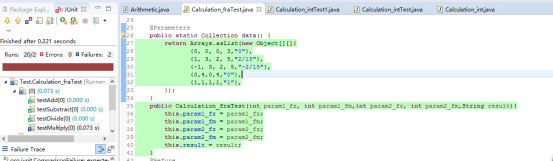
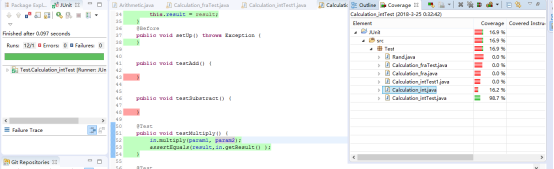
（以整数和分数的乘法为例）原项目的单元测试分别对整数和分数的加减乘除进行测试，每个测试用了五个用例。

2、改进分析

2.1改善部分

• 修改的代码中加入多操作符的运算
• 加入支持括号优先级运算
• 对表达式进行去重

2.2思维导图

2.3支持括号优先级运算和多操作符运算

2.4算式去重

• 暂时还没实现，但是写的算法大概如下：

 int Isomorphic(Tree t1,Tree t2){
	 if((t1==NULL)&&(t2==NULL))return 1;//都为空
	 if(((t1==NULL)&&(t2!=NULL))||((t1!=NULL)&&(t2==NULL))) return 0;//一个为空另一个不为空
	 if(t1->root!=t2->root) return 0;//根节点的值不一样
	 if((t1->lchild==NULL)&&(t2->lchild==NULL)) return Isomorphic(t1->lchild,t2->rchild);
	 if(((t1->lchild!=NULL)&&(t2->lchild!=NULL))&&(t1->lchild->data==t2->lchild->data))//没有交换
		 return (Isomorphic(t1->lchild,t2->lchild)&&Isomorphic(t1->rchild,t2->rchild));//如果两个都不为空且左儿子相等，应该递归的找左对应左，右对应右
	 else
		 return (Isomorphic(t1->lchild,t2->rchild)&&Isomorphic(t1->rchild,t2->lchild));//否则就是交换了，递归的判断左对应右，右对应左

 };

2.5测试用例

• 新功能测试用例
  
  

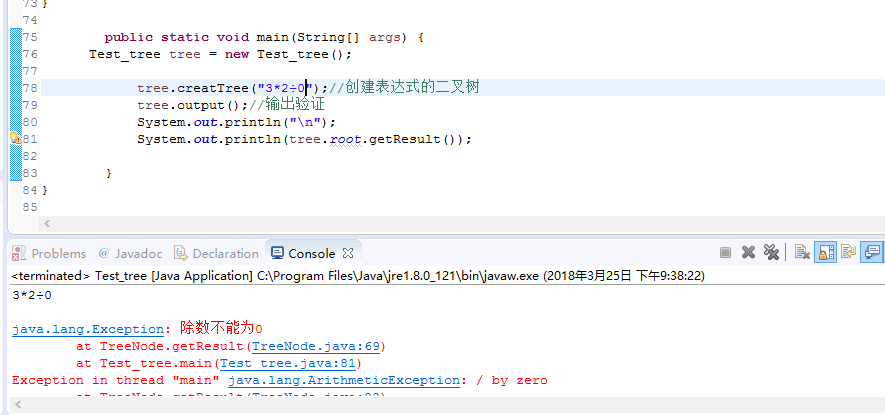
• 改进

3、附加题

3.1支持乘方运算

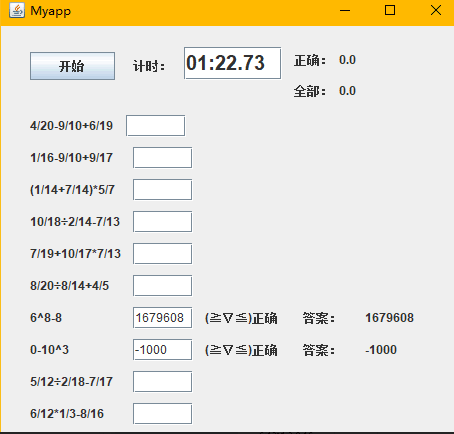
三、代码展示

• QA_List 类

public class QA_List {

	public static int i;
	public static List<String> Qusetion=new ArrayList<String>();
	public static List<String> Answer=new ArrayList<String>();
	public QA_List(){
		for(int a=0;a<i;a++)
	    {
	        //boolean x= new Random().nextBoolean();
	        //Arithmetic hh = new Arithmetic(x);
	        BinaryTree bTree;  
	       // for(int m = 0; m < i; m++){  
	            bTree = new BinaryTree(2);//随机生成数与表达式的数字个数有关  
	            bTree.createBTree();  
	            String result = bTree.CalAndVal();
	            if(result.contains("/")){
	            	if(Compute.Trans(result)[0].equals("0")){
	            		result="0";
	            	}else if(Compute.Trans(result)[1].equals("1")){
	            		result=Compute.Trans(result)[0];
	            	}
	            }
	            Answer.add(result);
	        	Qusetion.add(bTree.toString());
	            //System.out.println(bTree.toString() + "=" + result);  
	        //}  
	        /*String int_str = hh.int_operation();
	        String fra_str = hh.fra_operation();
	        if(x==true)
	        {
	        	Answer.add(int_str);
	        	Qusetion.add(hh.toString());
	        }
	        	
	        if(x==false)
	        {
	        	Answer.add(fra_str);
	        	Qusetion.add(hh.toString());
	        }*/
	    }
     for(int a=0;a<(10-i);a++){
     	Answer.add("");
     	Qusetion.add("");
     }
	}
	 
}

• BinaryTree 类

public class BinaryTree   
{  
      
    private TreeNode root;  
    private int num;  
    private ArrayList<TreeNode> opeList = new ArrayList<TreeNode>();  
      
    public BinaryTree(int num){  
        this.num = num;  
    }  
      
    public int getNum(){  
        return num;  
    }  
      
    public void setNum(int num){  
        this.num = num;  
    }  
      
    public void setTreeNode(TreeNode root){  
        this.root = root;  
    }  
      
      
    /** 
     * 获取最终的表达式，必须在CalAndVal()方法后调用 
     *  
     * @return str 
     */  
    public String toString(){  
        String str = root.toString();  
        str = str.substring(1, str.length()-1);  
        return str;  
    }  
      
    /** 
     * 计算并验证表达式 
     *  
     * @return result 
     */  
    public String CalAndVal(){  
        return root.getResult();  
    }  
      
    /** 
     * 计算二叉树的深度(层数)  
     *  
     * @return deep 
     */  
    public int getDeep(){  
        int i = this.num;  
        int deep = 2;  
        while(i/2 > 0){  
            deep++;  
            i /= 2;  
        }  
        return deep;  
    }  
      
    /** 
     * 生成二叉树 
     *  
     */  
    public void createBTree(){  
        TreeNode lchild, rchild, lnode, rnode;  
        int ran= Ran.getNumber(2),x,y;
        if(num == 1){
        	if(ran==0){
        		lchild = new TreeNode(String.valueOf(Ran.getNumber(10)), null, null);  
                rchild = new TreeNode(String.valueOf(Ran.getNumber(10)), null, null);  
        	}
        	else{
        		x=Ran.getNumber(9)+1;
        		y=Ran.getNumber(20)+1;
        		for(int j=0;y<=x;j++){
        			y=Ran.getNumber(20)+1;
        		}
        		lchild = new TreeNode(String.valueOf(x)+"/"+String.valueOf(y), null, null); 
        		x=Ran.getNumber(9)+1;
        		y=Ran.getNumber(20)+1;
        		for(int j=0;y<=x;j++){
        			y=Ran.getNumber(20)+1;
        		}
                rchild = new TreeNode(String.valueOf(x)+"/"+String.valueOf(y), null, null); 
        	}
            root = new TreeNode(String.valueOf(Ran.getOperator()), lchild, rchild);  
        }  
        else{  
            int num1 = 0;  
            int n = getDeep() - 3;  
            boolean[] place = Ran.getChildPlace(num);  
            root = new TreeNode(String.valueOf(Ran.getOperator()), null, null);  
            opeList.add(root);  
            for(int i = 0; i < n; i++){  
                for(int j = 0; j < (int)Math.pow(2, i); j++, num1++){  
                    lchild = new TreeNode(String.valueOf(Ran.getOperator()), null, null);  
                    rchild = new TreeNode(String.valueOf(Ran.getOperator()), null, null);  
                    opeList.get(j + num1).setChild(lchild, rchild);  
                    opeList.add(lchild);  
                    opeList.add(rchild);  
                }  
            }  
            for(int i = 0; i < place.length; i++){  
                if(place[i]){  
                	if(ran==0){
                		lnode = new TreeNode(String.valueOf(Ran.getNumber(10)), null, null);  
                        rnode = new TreeNode(String.valueOf(Ran.getNumber(10)), null, null);  
                	}
                	else{
                		x=Ran.getNumber(9)+1;
                		y=Ran.getNumber(20)+1;
                		for(int j=0;y<=x;j++){
                			y=Ran.getNumber(20)+1;
                		}
                		lnode = new TreeNode(String.valueOf(x)+"/"+String.valueOf(y), null, null); 
                		x=Ran.getNumber(9)+1;
                		y=Ran.getNumber(20)+1;
                		for(int j=0;y<=x;j++){
                			y=Ran.getNumber(20)+1;
                		}
                        rnode = new TreeNode(String.valueOf(x)+"/"+String.valueOf(y), null, null); 
                	}
                    if(i%2 == 0){  
                        lchild = new TreeNode(String.valueOf(Ran.getOperator()), lnode, rnode);  
                        opeList.add(lchild);  
                        opeList.get(num1).setLchild(lchild);  
                    }  
                    else{  
                        rchild = new TreeNode(String.valueOf(Ran.getOperator()), lnode, rnode);  
                        opeList.add(rchild);  
                        opeList.get(num1).setRchild(rchild);  
                    }  
                }  
                else{  
                    if(i%2 == 0){  
                    	if(ran==0){
                    		lchild=new TreeNode(String.valueOf(Ran.getNumber(10)), null, null);         
                    	}
                    	else{
                    		x=Ran.getNumber(9)+1;
                    		y=Ran.getNumber(20)+1;
                    		for(int j=0;y<=x;j++){
                    			y=Ran.getNumber(20)+1;
                    		}
                    		lchild = new TreeNode(String.valueOf(x)+"/"+String.valueOf(y), null, null); 
                    	}  
                        opeList.get(num1).setLchild(lchild);  
                    }  
                    else{  
                
                         	if(ran==0){
                         		rchild = new TreeNode(String.valueOf(Ran.getNumber(10)), null, null);          
                         	}
                         	else{
                         		x=Ran.getNumber(9)+1;
                         		y=Ran.getNumber(20)+1;
                         		for(int j=0;y<=x;j++){
                         			y=Ran.getNumber(20)+1;
                         		}
                         		rchild = new TreeNode(String.valueOf(x)+"/"+String.valueOf(y), null, null); 
                         	}  
                        opeList.get(num1).setRchild(rchild);  
                    	 
                    }  
                num1 = num1 + i%2;  
            }  
        }  
    }  
}  
}

- TreeNode类
public class TreeNode {  
      
    private String str;  
    private TreeNode rchild = null;  
    private TreeNode lchild = null;  
      
    public TreeNode(String str){  
        this.str = str;  
    }  
      
    public TreeNode(String str, TreeNode lchild, TreeNode rchild){  
        this.str = str;  
        this.rchild = rchild;  
        this.lchild = lchild;  
    }  
      
    public void setChild(TreeNode lchild, TreeNode rchild){  
        this.lchild = lchild;  
        this.rchild = rchild;  
    }  
      
    public TreeNode getRchild() {    
        return rchild;    
    }    
    public void setRchild(TreeNode rchild) {    
        this.rchild = rchild;    
    }    
    public TreeNode getLchild() {    
        return lchild;    
    }    
    public void setLchild(TreeNode lchild) {    
        this.lchild = lchild;    
    }  
      
    public String getStr(){  
        return str;  
    }  
      
    /** 
     * 获取每个节点的运算结果，并检验除法 
     * 1)除数为0 
     * 2)不能整除 //不考虑，允许分数的出现
     * 出现以上两种情况的话将该运算符转换成其他三种运算符 
     *  
     * @return result 
     */  
    public String getResult(){  
    	Compute com=new Compute();
        if(hasChild()){  
            switch(str){  
                case "+":
                	if(!getLchild().getResult().contains("/"))
                		return String.valueOf(Integer.parseInt(getLchild().getResult()) + Integer.parseInt(getRchild().getResult())); 
                	else
                		return com.Add(getLchild().getResult(),getRchild().getResult());
                case "-":  
                	if(!getLchild().getResult().contains("/"))
                    	return String.valueOf(Integer.parseInt(getLchild().getResult()) - Integer.parseInt(getRchild().getResult()));  
                	else
                		return com.Subtract(getLchild().getResult(),getRchild().getResult());
                case "*":  
                	if(!getLchild().getResult().contains("/"))
                    	return String.valueOf(Integer.parseInt(getLchild().getResult()) * Integer.parseInt(getRchild().getResult()));  
                	else	
                		return com.Multiply(getLchild().getResult(),getRchild().getResult());
                case "÷":  
                    if(getRchild().getResult().equals("0")||getRchild().getResult().contains("0/")){  
                        while(str.equals("÷")){  
                            str = String.valueOf(Ran.getOperator());  
                        }  
                        return this.getResult();  
                    }  
                    /*else if(Integer.parseInt(getLchild().getResult()) % Integer.parseInt(getRchild().getResult()) != 0){  
                        while(str.equals("/")){  
                            str = String.valueOf(Ran.getOperator());  
                        }  
                        return this.getResult();  
                    } */ 
                    if(!getLchild().getResult().contains("/")){
                		if(Integer.parseInt(getLchild().getResult()) % Integer.parseInt(getRchild().getResult()) != 0){  
                            while(str.equals("÷")){  
                                str = String.valueOf(Ran.getOperator());  
                            }  
                            return this.getResult();  
                        }
                		//return String.valueOf(Integer.parseInt(getLchild().getResult()) / Integer.parseInt(getRchild().getResult())); 
                	}
                    else{
                    	if(!getLchild().getResult().contains("/")){
               
                    		return String.valueOf(Integer.parseInt(getLchild().getResult()) / Integer.parseInt(getRchild().getResult())); 
                    	}
                    		
                    	else{
                    		
                    		return com.Divide(getLchild().getResult(),getRchild().getResult());
                    	}
                    		
                    }
                        
            }  
        }  
        return str;  
    }       
      
    /** 
     * 先对每个运算式添加括号，然后根据去括号法则，去掉多余的子式的括号 
     *  
     * @return string 
     */  
    public String toString(){  
        String Lstr = "", Rstr = "", Str = "";  
        if(hasChild()){  
            //右子树如果有孩子，说明右子树是一个表达式，而不是数字节点。  
            if(getRchild().hasChild()){                           
                //判断左邻括号的运算符是否为'/'  
                if(str.equals("÷")){  
                    //获取右子树的表达式，保留括号  
                    Rstr = getRchild().toString();                
                }  
                //判断左邻括号的运算符是否为'*'或'-'  
                else if(str.equals("*") || str.equals("-")){  
                    //判断op是否为'+'或'-'  
                    if(getRchild().str.equals("+") || getRchild().str.equals("-")){   
                        Rstr = getRchild().toString();            
                    }  
                    else{  
                        //获取右子树的表达式，并且去括号   
                        Rstr = getRchild().toString().substring(1, getRchild().toString().length()-1);    
                    }  
                }  
                else{  
                    //右子树除此之外都是可以去括号的。  
                    Rstr = getRchild().toString().substring(1, getRchild().toString().length()-1);        
                }  
            }  
            else{  
                Rstr = getRchild().str;  
            }  
            //左子树的情况同右子树类似  
            if(getLchild().hasChild()){                                               
                if(str.equals("*") || str.equals("÷")){  
                    if(getLchild().str.equals("+") || getLchild().str.equals("-")){  
                        Lstr = getLchild().toString();  
                    }  
                    else{  
                        Lstr = getLchild().toString().substring(1, getLchild().toString().length()-1);  
                    }  
                }  
                else{  
                    Lstr = getLchild().toString().substring(1, getLchild().toString().length()-1);  
                }  
            }  
            else{  
                Lstr = getLchild().str;  
            }  
            //获取当前的运算式，并加上括号  
            Str = "(" + Lstr + str + Rstr + ")";                                      
        }  
        else{  
            //若没有孩子，说明是数字节点，直接返回数字  
            Str = str;  
        }  
        return Str;  
    }  
      
    public boolean hasChild(){  
        if(lchild == null && rchild == null)  
            return false;  
        else  
            return true;  
    }  
}  

四、程序运行

• 开始界面，选择语言切换和填写要做的题数

• 进入计时界面，点击计时开始做题
  

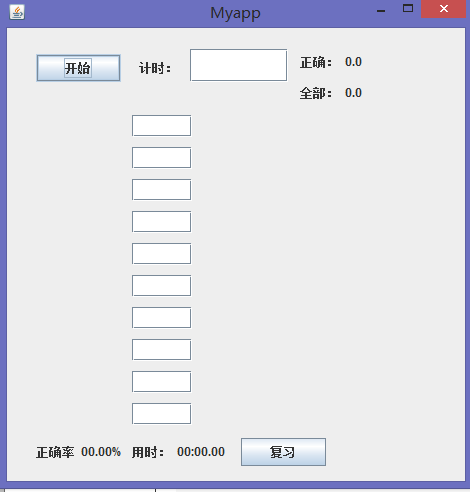
• 回答题目，判断对错
  

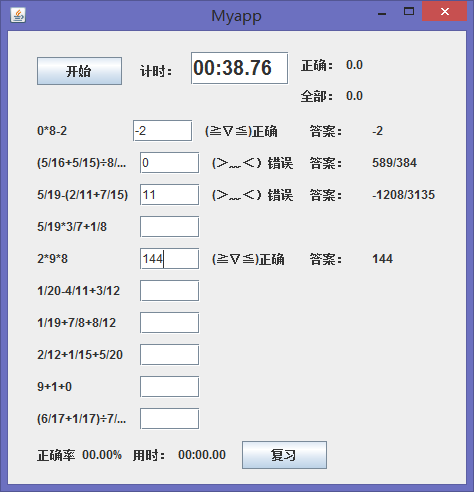
• 点击复习，回到主界面，重新选择做的题数对错题进行重新计算

五、小结感受

1、结对照片

2、PSP表格

PSP2.1 | 个人开发流程 | 预估耗费时间（分钟）| 实际耗费时间（分钟）

• |- |- |-
  ·Planning | 计划 | 8 | 15
  ·Estimate | 明确需求和其他相关因素，估计每个阶段的时间成本 | 8 | 6
  ·Development | 开发 | 240 | 284
  ·Analysis | 需求分析 (包括学习新技术）| 6 | 10
  ·Design Spec | 生成设计文档 | 5 |10
  ·Design Review | 设计复审| 4 | 15
  ·Coding Standard | 代码规范 | 5 | 10
  ·Design | 具体设计 | 20 | 30
  ·Coding | 具体编码 | 288 | 300
  ·Code Review | 代码复审 | 20 | 30
  ·Test | 测试（自我测试，修改代码，提交修改）| 15 | 25
  ·Reporting | 报告 | 9 | 10
  · | 测试报告 | 3 | 5
  · | 计算工作量 | 2 | 1
  · | 并提出过程改进计划 | 3 | 3

3、结对编程真的能够带来1+1>2的效果吗？通过这次结对编程，请谈谈你的感受和体会。

• 两个人结对编程确实会在一些问题上考虑的比较周全，而且分工合作效率会比较高，但是1+1>2的效果我觉得不是一次结对编程就能有所显现的，第一次还在磨合阶段，其实很多时间都花在讨论上。
• 在原本的代码上进行修改，我觉得比自己写一个基本的四则运算程序还要难，有些代码是基本上都要重新写，会用到二叉树也是因为老师在群里面说到去重可以用到树的最小表示法而受到启发。因为数据结构是大二上学的，有些知识点都忘了，所以花了很多的时间复习以前的知识，如何建立树和遍历树等等。
• 然后界面的代码觉得还在netbean上操作会比较方便