【深度学习】神经网络入门

0.神经网络模型

　　一个简单的神经网络，其含括3个层，输入层，隐藏层，输出层。

　　输入层（Input layer）：用于输入样本数据x；

　　隐藏层（Hidden layer）：用于处理输入的数据，例如降维，突出数据特征，其中可能含有多个层；

　　输出层（Output layer）：输入数据由隐藏层传入，经过计算，再输出最终结果。

　　其架构图[1]如下：

 

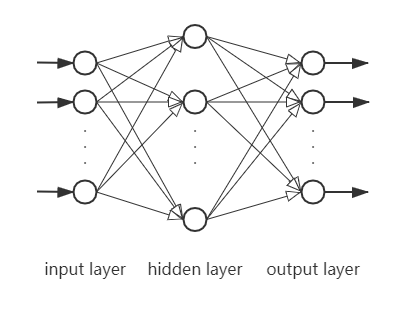
1. 线性模型

　　关于如何入手，由单一特征模型（1.1）开始。

1.1. 回归直线方程：

　　假设现在有一波散点，呈一定线性规律分布在x、y轴上，此时希望求出一条直线，使直线尽量离所有散点距离最近。可以设这条直线是 y = wx + b，那么如何确定w与 b 呢？

       此时的 w 就是对 x 映射到 y 数值影响的程度，也就是权重（weight）；而b是偏差值（bias），可能为任意实数。

　　我们最终的目的是，求出一条尽量贴切所有散点（这个过程是回归 [0] ，是拟合 [1] 的一种）的直线，那么这条线 y_预 与实际值 y_实 之间的差距，必然希望是尽可能最小，而关于如何计算这个差距，那就有很多种计算方法，要看具体场景选择哪个距离函数。这个表示差距函数就是损失函数（loss function不同翻译也叫代价函数），设其为 f(x) ，有：

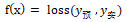
　　设m为样本总数，以误差平方和均值的一半作为 loss：

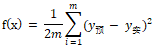
　　让损失最小，即求函数f(x)最小值，可以求导。

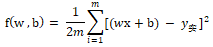
　　拆开上式，再对w、b求偏导，令偏导函数结果为0，可以计算得出w、b，不赘述。对于计算机来说，求两个、三个变量的多项式，都是容易的，但实际的神经网络其参数都是成千上万的，要找所有导数为0的点，这样计算量就很大。

 

[0] 回归（regression）：

研究一组随机变量与另一组变量之间关系的统计分析方法。其有具体的方法，如一元线性回归、多元线性回归、logistic回归、Poisson回归等。

[1] 拟合（fitting）：

把平面上一系列的点，用一条光滑的曲线连接起来。拟合是一种广泛概念，如回归、插值和逼近等，都是拟合。

 

1.2. 反向传播（Backward Pass）

　　由于处理的损失函数，是可微的，可以计算梯度，来反方向更新权重，每一次反向都使损失变小一点。

 

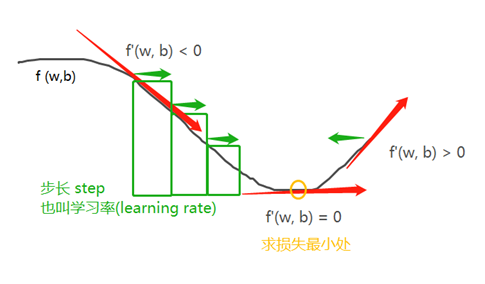
用 i 表示权重更新的迭代次数，有：

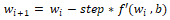  [2]

 

 　　整体过程如下：

　　(1) 取训练样本 x 和对应目标 y 组成的数据批量；

　　(2) 把 x 放入网络（可以设取随机的权重），得到预测值 y_预；

　　(3) 计算 y_预 与 y 之间的距离；

　　(4) 计算损失相对于网络参数的梯度（反向传播（backward pass））；

　　(5) 将参数沿梯度反方向移动一点，比如 w - = step * f '，从而使这批数据上的损失减小一点。

　　这种方法叫做随机梯度下降（stochastic gradient descent），简称SGD。

　　SGD还有很多变体，其区别在于计算下一次权重更新时，还要考虑上一次权重更新，而不是仅考虑当前梯度值。例如有带动量的SGD、Adagrad、RMSProp等变体。这些变体被称作优化方法（optimization method）或优化器（optimizer）。其中带动量的SGD（后面再研究）解决了SGD两个问题：收敛速度和局部极小点。

 

　　对于多特征问题（设n个特征），可以将目标函数设为式①，其权重的修正规则与单特征的训练规则一样，但在层次的每次输出，都需要做一些处理，下节描述。

[式1]

 [2] 梯度上升法与梯度下降法是一样的，不过前者是求函数最大值，后者求函数最小值。因此，对应的梯度上升公式可以这样写：

 

 

2. 非线性模型

　　线性模型与非线性模型，其最大区别在于，前者图像斜率不变，后者图像斜率会变化。进一步解释 [3]，Y与X之间不存在线性关系，但Y与参数β之间存在线性关系，例如：

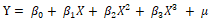
　　对于解决多特征问题，纯粹使用 [式1] 的权重和，那么层次中就只能学习到输入数据的线性变化（仿射变换）：该层的假设空间是从输入数据到16位空间所有可能的线性变换集合，这种假设空间非常有限，因为即使多个层次的线性层堆叠实现的依然是线性运算，不会拓展到假设空间，那么就无法利用多个表示层的优势。

　　如果能糅合进非线性元素，拟合结果可能会有所改善。这个非线性元素就是激活函数（activation function），不同翻译也有叫激励函数。

 

[3] 详可见：

https://baike.baidu.com/item/%E9%9D%9E%E7%BA%BF%E6%80%A7%E6%A8%A1%E5%9E%8B/10463547?fr=aladdin