2.4小时教你精通RSA加解密、签名验签算法

2.4小时教你精通RSA加解密、签名验签算法

现在很流行什么24小时精通xxx，我觉得24小时太久，不如试试2.4小时。   
而且我敢说，认真看完这个，真的是可以精通，不是入门哦。

---

RSA简介

RSA加密算法是1977年由罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）一起提出的。   
RSA是非对称算法,握有一对公私钥。使用公钥加密,私钥解密。使用私钥签名,公钥验签。

---

RSA加密数学原理

    RSA加密采用了大质数难以分解的原理来进行加密和解密。至于更深的原理需要具备一些数论的知识。这里可以先不管。
    对极大整数做因数分解的难度决定了RSA算法的可靠性。换言之，对一极大整数做因数分解愈困难，RSA算法愈可靠。因此RSA具有1024,2048,3072,4096这4
种长度的密钥.其中1024位的已经不鼓励使用了.
要学会RSA加密,只需要知道以下2个公式,就掌握了基本内功：

pow(x, e) % n = y; // x的e次方模n得到y
pow(y, d) % n = x; // y的d次方模n得到x

通过公式1就可以将x转换成y,通过公式2就可以将y转换成x。实际上,这就是加密和解密的过程。看起来十分简单。
那么加密使用公钥,公钥就可以理解成e和n的组合。解密使用私钥,私钥就是d和n的组合。
记住：公钥 == (e, n), 私钥 == (d, n)
那么e,n,d都是什么呢？怎么产生的呢？步骤如下，产生2个大的素数p和q,为了方便解说,咱们用2个小的素数来替代。

1. 假设p = 13, q = 19
2. 计算素数的乘积。 n = p * q = 247。247这个整数用16进制表示就是0xF7,一共8个bit,那么这就可以称为RSA8的密钥.比RSA2048短很多很多。
3. 计算欧拉函数 φ = (p - 1)(q - 1) = 216
4. e固定取值65537, e和φ是互质的.(在RSA规则中e是固定的,但是从算法角度可以取任意和φ互质的数,为了直观,假设是17)
5. 找到一个d可以满足e * d = 1 (mod φ)。 也就是找到一个整数d，可以使得e*d被φ除的余数为1
   这个公式5实际上等于e * d - 1 = kφ.实际上就是e * a + φ * b = 1的公式求解。可以用扩展欧几里德算法求解。
   在p=13,q=19,e=17的情况下,则17a+216b=1,我们可以得到其中一个答案a=89,b=-7.那么d就等于这个a,也就是d=89。

假设现在有一个明文数字是101，我们加密后，就是101的17次方模247，也就是密文结果是225
然后用密文225去解密，也就是225的89次方模247，得到明文101

    @Test
    public void testRSA() {
        int plainText = 101;
        int n = 247;
        int e = 17;
        int d = 89;
        /* 加密：plain的e次方,模n*/
        BigInteger cipher = BigInteger.valueOf(plainText).modPow(BigInteger.valueOf(e), BigInteger.valueOf(n));
        log.debug("{}", cipher.intValue());
        /* 解密：cipher的d次方,模n*/
        BigInteger plain = cipher.modPow(BigInteger.valueOf(d), BigInteger.valueOf(n));
        log.debug("{}", plain.intValue());
        Assertions.assertEquals(plain.intValue(), plainText);
    }

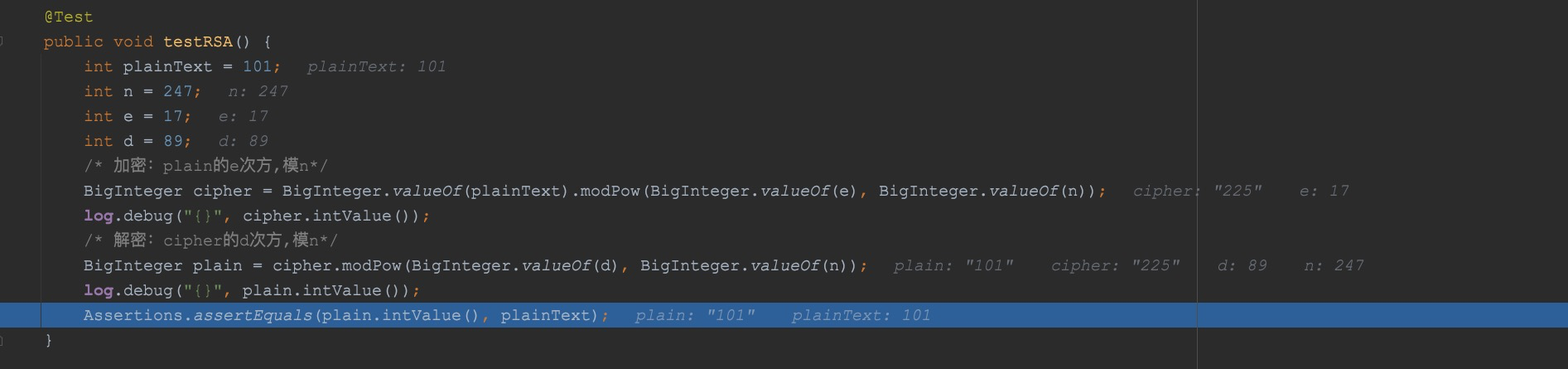
以上就是加解密的基本原理了。
但是基本原理仅仅是实验室水准,拿出来压根没办法用!!!
实际加密还受到很多PKI体系的规则约束,比如PKCS#1。

PKCS#1

    Public-Key Cryptography Standards (PKCS)是由美国数据安全公司及其合作伙伴制定的一组公钥密码学标准,
其中包括证书申请、证书更新、证书作废表发布、扩展证书内容以及数字签名、数字信封的格式等方面的一系列相关协议。
大家可以认为这是实际上的国际标准。
    对称密钥往往很简单,比如一个16个字节的AES密钥,那就是光秃秃16个字节,可以用base64.key的格式保存起来就OK了,很粗暴。
对称密钥只要长度正确,往往可以用于不同的算法,都是通用的。
    而非对称密钥就复杂多了,一个非对称密钥只能用于它自身的算法,为了可以精准识别,非对称密钥数据往往还包含了各种信息。
为了把这些密钥信息和密钥数据柔和在一起,可以有很多方法. 我们现在往往可以使用Json、XML、Yaml等方式.但是早期没有这些,因此PKCS组织指定了一种标准协议,叫ASN.1。
咱们这里只对ASN.1说一个简短的介绍,更深的读者自己去学习。
    ASN.1就是一个Target-Length-Value(TLV)的结构,简单的说,举个例子,现在我要放一个oid到密钥信息中:

1. 就先放一个字节的oid的target标记;
2. 再放一个字节的oid的长度;
3. 最后放N个字节的oid的内容,就OK了。

---

    RSA密钥常见的格式主要如下：
公钥：PKCS#1, X.509
私钥：PKCS#1, PKCS#8
PKCS#1的RSA公钥格式：

RSAPublicKey ::= SEQUENCE {
   modulus INTEGER , -- n
   publicExponent INTEGER -- e
}

PKCS#1的RSA私钥格式：

RSAPrivateKey ::= SEQUENCE {
    version Version ,
    modulus INTEGER , -- n
    publicExponent INTEGER , -- e
    privateExponent INTEGER , -- d
    prime1 INTEGER , -- p
    prime2 INTEGER , -- q
    exponent1 INTEGER , -- d mod (p-1)
    exponent2 INTEGER , -- d mod (q-1)
    coefficient INTEGER , -- (inverse of q) mod p
    otherPrimeInfos OtherPrimeInfos OPTIONAL
}

可以发现这本质上和JSON,XML都差不多。本来私钥只需要放n和d就够了，但是为了方便计算,把中间的各种变量和公钥数据都放进去了,因此得到RSA的私钥就可以直接得到公钥了。
为了把密钥变成容易复制的文本和容易被人类分辨的。因此会将二进制的ASN.1协议组装好的数据用base64编码后变成可见文本。但是这只解决了复制问题,人类看起来还是不知道是什么密钥。
因此还有一种PEM格式.就是在BASE64文本的头尾各加一行字符串,这样人类就可以看懂了。
PKCS#1的RSA公钥PEM格式：

-----BEGIN RSA PUBLIC KEY-----
BASE64编码的密钥文本
-----END RSA PUBLIC KEY-----

PKCS#1的RSA私钥PEM格式：

-----BEGIN RSA PRIVATE KEY-----
BASE64编码的密钥文本
-----END RSA PRIVATE KEY-----

早期这样就够用了,因为这是第一代标准,因此叫PKCS#1。但是后来非对称密钥出现了椭圆曲线算法,这样RSA就不是唯一的非对称算法了,就出现了不统一的情况。
于是随着时代的发展,推出了X.509和PKCS#8的标准。以后所有的标准公钥都必须符合X.509,而标准私钥都必须符合PKCS#8。那是怎么做到的呢？原理很简单,在
PKCS#1的标准上加一个头信息,头信息中标明改密钥是什么算法,然后就可以走不同的分支了。于是我们看看格式内容：
X.509的RSA公钥格式：

RSAPublicKey ::= SEQUENCE {
   algorithm AlgorithmIdentifier , // 这就是增加的头信息
   publicKey RSAPublicKey  // 这就是PKCS#1的RSA公钥的内容
}

PKCS#8的RSA私钥格式：

PrivateKey ::= SEQUENCE {
    version Version ,  // 这就是增加的头信息
    privateKeyAlgorithm PrivateKeyAlgorithmIdentifier , // 这也是增加的头信息
    privateKey RSAPrivateKey // 这就是PKCS#1的RSA私钥的内容
}

同样的为了人类方便识别,也有对应的PEM格式的文本头尾：
X.509的RSA公钥PEM格式：

-----BEGIN PUBLIC KEY-----
BASE64编码的密钥文本
-----END PUBLIC KEY-----

PKCS#8的RSA私钥PEM格式：

-----BEGIN PRIVATE KEY-----
BASE64编码的密钥文本
-----END PRIVATE KEY-----

看见没？区别就是少了字符串RSA,因为是通用的了嘛！

填充规则

介绍完基本的PKCS体系后,咱们继续进行密码算法计算,来点干货.在加密数学原理中,我们可以发现被加密的明文其实是不能超过密钥长度的,为什么呢？
因为e的值必须比n小,在数论体系中才可以满足这个公式。那么为了方便识别明文，PKCS规定了RSA加密的填充规则,我们叫PKCS1Padding,现在一般使用的是
V1.5版本。(还有OAEP等padding规则,此处不展开说).
PKCS规定,使用RSA公钥加密的时候,需要在明文前加一个0x00的备用字节,然后加一个0x02,表示是公钥加密,然后加一段没有0的随机数据,然后加一个0x00结尾,然后加明文数据.
让这些长度恰好等于密钥长度。以RSA2048为例,密钥长2048比特,也就是256个字节.
那么假设我们需要加密100个字节的明文,在加密前,需要人为填充成如下结构

新明文 == 0x00 + 0x02 + (256 - 103)字节的非0随机数 + 0x00 + (100)字节的原明文

这样新明文就恰好是256个字节了。因此实际使用中,明文的长度不能超过密钥长度减去3字节。解密后再根据这个规则反推出真正的明文。

talk is cheap, show you the code

光说不练假把式,流于表面,咱们上代码来模拟一次用自己实现的算法加密,然后用JDK自己去解密,看看能不能成功？
先实现一下这个加密填充规则：

    private static final byte ENCRYPT_PAD_FLAG = (byte) 0x02;
    private static final byte HEAD = (byte) 0x00;
    private static final byte TAIL = (byte) 0x00;
    /**
     * RSA公钥加密时,填充明文到密钥长度
     *
     * @param msg     数据
     * @param keySize 密钥bit位数
     * @return 填充后的数据
     */
    private byte[] padEncrypt(byte[] msg, int keySize) {
        int keyLen = keySize / Byte.SIZE;
        int msgLen = msg.length;
        int padLen = keyLen - msgLen - 3; // 3 == 0x00+0x02+0x00
        byte[] pad = getNoZeroRand(padLen);
        ByteBuffer buf = ByteBuffer.allocate(keyLen);
        buf.put(HEAD);
        buf.put(ENCRYPT_PAD_FLAG);
        buf.put(pad);
        buf.put(TAIL);
        buf.put(msg);
        return buf.array();
    }

    /**
     * 模拟产生没有0的随机数
     *
     * @param len 长度
     * @return 随机数
     */
    private byte[] getNoZeroRand(int len) {
        byte[] buf = new byte[len];
        ThreadLocalRandom.current().nextBytes(buf);
        for (int i = 0; i < len; i++) {
            while (buf[i] == 0) {
                byte[] tmp = new byte[1];
                ThreadLocalRandom.current().nextBytes(tmp);
                buf[i] = tmp[0];
            }
        }
        return buf;
    }

---

加密实战

然后我们使用JDK产生一对2048的RSA密钥,自己加密,JDK解密

    @Test
    public void testMeEncryptAndJceDecrypt() throws NoSuchAlgorithmException, NoSuchPaddingException, InvalidKeyException, IllegalBlockSizeException, BadPaddingException {
        KeyPairGenerator generator = KeyPairGenerator.getInstance(RSA);
        generator.initialize(_2048);
        KeyPair pair = generator.generateKeyPair();
        RSAPublicKey pk = (RSAPublicKey) pair.getPublic();
        RSAPrivateCrtKey sk = (RSAPrivateCrtKey) pair.getPrivate();
        BigInteger n = pk.getModulus();
        BigInteger e = pk.getPublicExponent();
        /* 模拟明文 */
        byte[] plainText = new byte[100];
        ThreadLocalRandom.current().nextBytes(plainText);
        log.debug("{}", Hex.toHexString(plainText));
        byte[] padPlainText = padEncrypt(plainText, _2048);
        /* 自己加密,cipherText == plainText^e % n */
        BigInteger plainInteger = new BigInteger(padPlainText);
        /* modPow()方法内置了基于数论的算法,比自己pow后再mod快很多很多很多很多 */
        BigInteger cipherInteger = plainInteger.modPow(e, n);
        byte[] cipherTextMy = cipherInteger.toByteArray();
        /* JCE解密 */
        Cipher cipher = Cipher.getInstance(RSA);
        cipher.init(Cipher.DECRYPT_MODE, sk);
        byte[] p = cipher.doFinal(cipherTextMy);
        Assertions.assertArrayEquals(plainText, p);
        log.debug("END");
    }

我们先用padEncrypt把随机产生的明文填充后,在使用e和n进行加密,最后用JDK进行解密，比对一致。

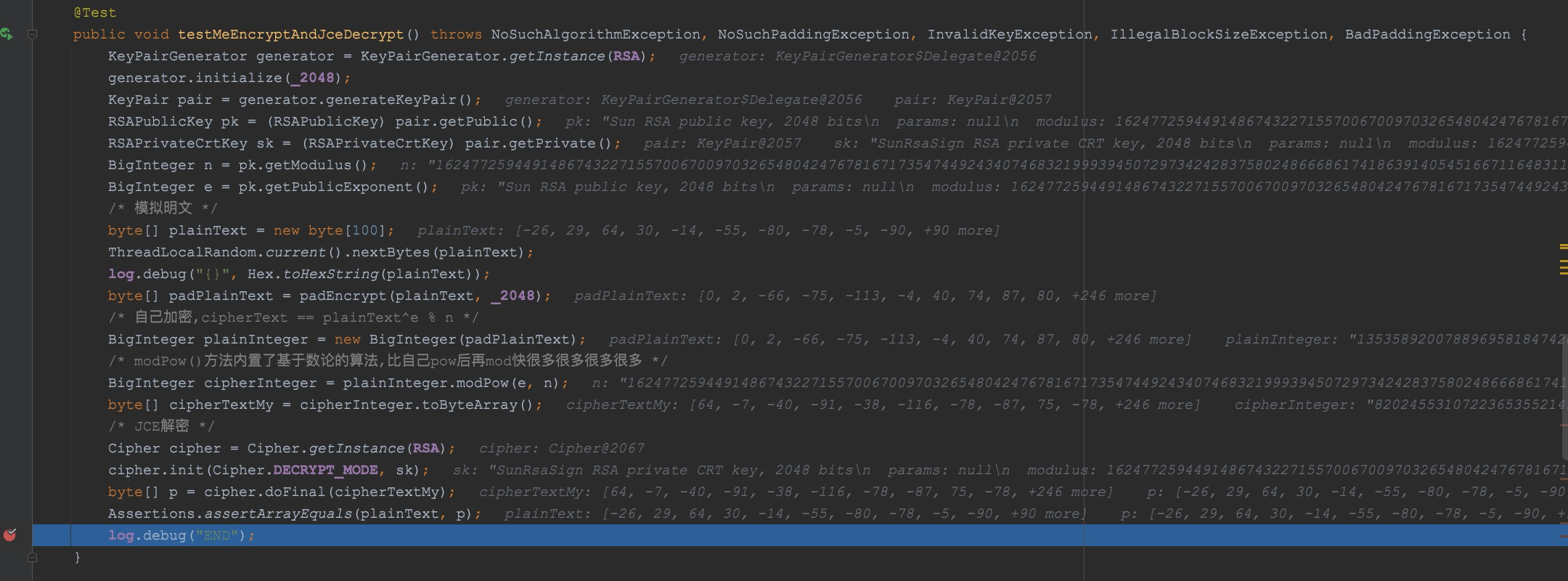
可以看见，完全一致。可以证明咱们的加密算法已经走出了实验室，完全可以用于实际场景。

总结一下：    
实际加密时要按规则把明文填充到密钥长度，因此加密后到密文长度肯定也是密钥长度，由于有随机数填充，那么密文每次都会不同（除非长度恰好只填充了规则里的3字节）    
为什么要让明文填充到密钥长度呢？是为了让数据尽可能长一点，加大被破解的难度。

---

签名实战

RSA除了用公钥加密数据,用私钥解密数据外。还可以用私钥签名数据,用公钥验签数据,来证明数据的合法性。
那么如何签名呢？
所谓签名其实就是用私钥加密,而验签就使用公钥解密。当然这个说法依然仅仅是实验室级别的,实际上的签名过程还是需要有好几步的,这样才符合PKCS规范。
常见的RSA签名算法有SHA256WithRSA、SHA128WithRSA、SHA1WithRSA等等,看到区别了吗？就是一个杂凑算法名+with+RSA。
是什么意思呢？简单的说,对一串数据进行RSA签名分4步：

1. 对数据进行杂凑计算,得到比较短的哈希值.(之前说过RSA加密只能加密很短的数据)
2. 对哈希值进行ASN.1编码,加上杂凑算法的国际OID,得到一串稍微长一点的DER数据
3. 对DER数据进行PKCS#1Padding填充到密钥长度(填充规则和公钥加密不同)
4. 使用私钥加密后得到签名值
       下面我们来说明一下：

• 计算HASH,没啥好说的,SHA256WithRSA就用SHA256算法计算哈希,XXXWithRSA就用XXX算法计算哈希
• ASN.1编码需要将XXX杂凑算法的OID编码进去,举个例子SHA256的国际OID是2.16.840.1.101.3.4.2.1
• 私钥签名填充规则和公钥加密填充规则不同,但是大体差不多。
  PKCS#1规定,使用RSA私钥签名的时候,需要在DER数据前加一个0x00的备用字节,然后加一个0x01,表示是私钥签名,然后加一段全是0xFF的数据,然后加一个0x00结尾,然后加DER数据.
  让这些长度恰好等于密钥长度。以RSA2048为例,密钥长2048比特,也就是256个字节.
  那么假设我们需要对100个字节的DER进行填充,在签名前,需要人为填充成如下结构

   新数据 == 0x00 + 0x01 + (256 - 103)个字节的0xFF + 0x00 + (100)字节的DER数据  

• 最后用私钥加密

talk is cheap, show you the code

以SHA256WithRSA签名算法为例。
我们先实现给哈希添加OID的编码：

    /**
     * 给哈希值加上oid等信息
     *
     * @param oid    oid
     * @param digest 哈希
     * @return DER数据
     * @throws IOException IO异常
     */
    public byte[] addOid(ObjectIdentifier oid, byte[] digest)
            throws IOException {
        DerOutputStream out = new DerOutputStream();
        new AlgorithmId(oid).encode(out);
        out.putOctetString(digest);
        DerValue result = new DerValue(DerValue.tag_Sequence, out.toByteArray());
        return result.toByteArray();
    }

    /**
     * 计算SHA-256
     * 
     * @param msg 消息
     * @return 杂凑
     * @throws NoSuchAlgorithmException 异常
     */
    private byte[] getSha256(byte[] msg) throws NoSuchAlgorithmException {
        MessageDigest digest = MessageDigest.getInstance(SHA256);
        return digest.digest(msg);
    }

使用ASN.1编码后的样子大概是这样的：

然后我们实现一下padding填充规则：

    private static final byte SIGN_PAD_FLAG = (byte) 0x01;
    private static final byte FF = (byte) 0xFF;
    /**
     * 签名填充
     *
     * @param msg 数据
     * @param keySize RSA密钥bit位数
     * @return 结果
     */
    private byte[] padSign(byte[] msg, int keySize) {
        int keyLen = keySize / Byte.SIZE;
        int msgLen = msg.length;
        int padLen = keyLen - msgLen - 3;
        byte[] pad = new byte[padLen];
        Arrays.fill(pad, FF);
        ByteBuffer buf = ByteBuffer.allocate(keyLen);
        buf.put(HEAD);
        buf.put(SIGN_PAD_FLAG);
        buf.put(pad);
        buf.put(TAIL);
        buf.put(msg);
        return buf.array();
    }

准备工作做完后就可以开始正餐了.我们来模拟一次用自己实现的算法进行签名,然后让JDK也去签名一次,如果完全一致,则说明成功,都不需要验签了。

    private static final String SHA256 = "SHA-256";
    private static final String SHA256_WITH_RSA = "SHA256WithRSA";
    @Test
    public void testMeSignAndJceVerify() throws NoSuchAlgorithmException, InvalidKeyException, SignatureException, IOException {
        KeyPairGenerator generator = KeyPairGenerator.getInstance(RSA);
        generator.initialize(_2048);
        KeyPair pair = generator.generateKeyPair();
        RSAPublicKey pk = (RSAPublicKey) pair.getPublic();
        RSAPrivateCrtKey sk = (RSAPrivateCrtKey) pair.getPrivate();
        /* 模拟数据 */
        byte[] plainText = new byte[50];
        ThreadLocalRandom.current().nextBytes(plainText);
        /* 用自己实现的算法签名 */
        /* 1.先用SHA256计算杂凑 */
        byte[] hash = getSha256(plainText);
        /* 2.ASN.1添加OID信息变成DER数据 */
        byte[] der = addOid(AlgorithmId.SHA256_oid, hash);
        /* 3.填充 */
        byte[] msg = padSign(der, _2048);
        /* 4.私钥加密最后的msg */
        BigInteger msgInteger = new BigInteger(msg);
        BigInteger v = msgInteger.modPow(sk.getPrivateExponent(), sk.getModulus()); // 私钥的d & n
        byte[] sign = v.toByteArray();
        log.debug("{}", Hex.toHexString(sign));
        /* JCE签名 */
        Signature signature = Signature.getInstance(SHA256_WITH_RSA);
        signature.initSign(sk);
        signature.update(plainText);
        byte[] sign1 = signature.sign();
        Assertions.assertArrayEquals(sign1, sign);
        /* JCE验签 */
        signature = Signature.getInstance(SHA256_WITH_RSA);
        signature.initVerify(pk);
        signature.update(plainText);
        boolean ret = signature.verify(sign);
        Assertions.assertTrue(ret);
    }

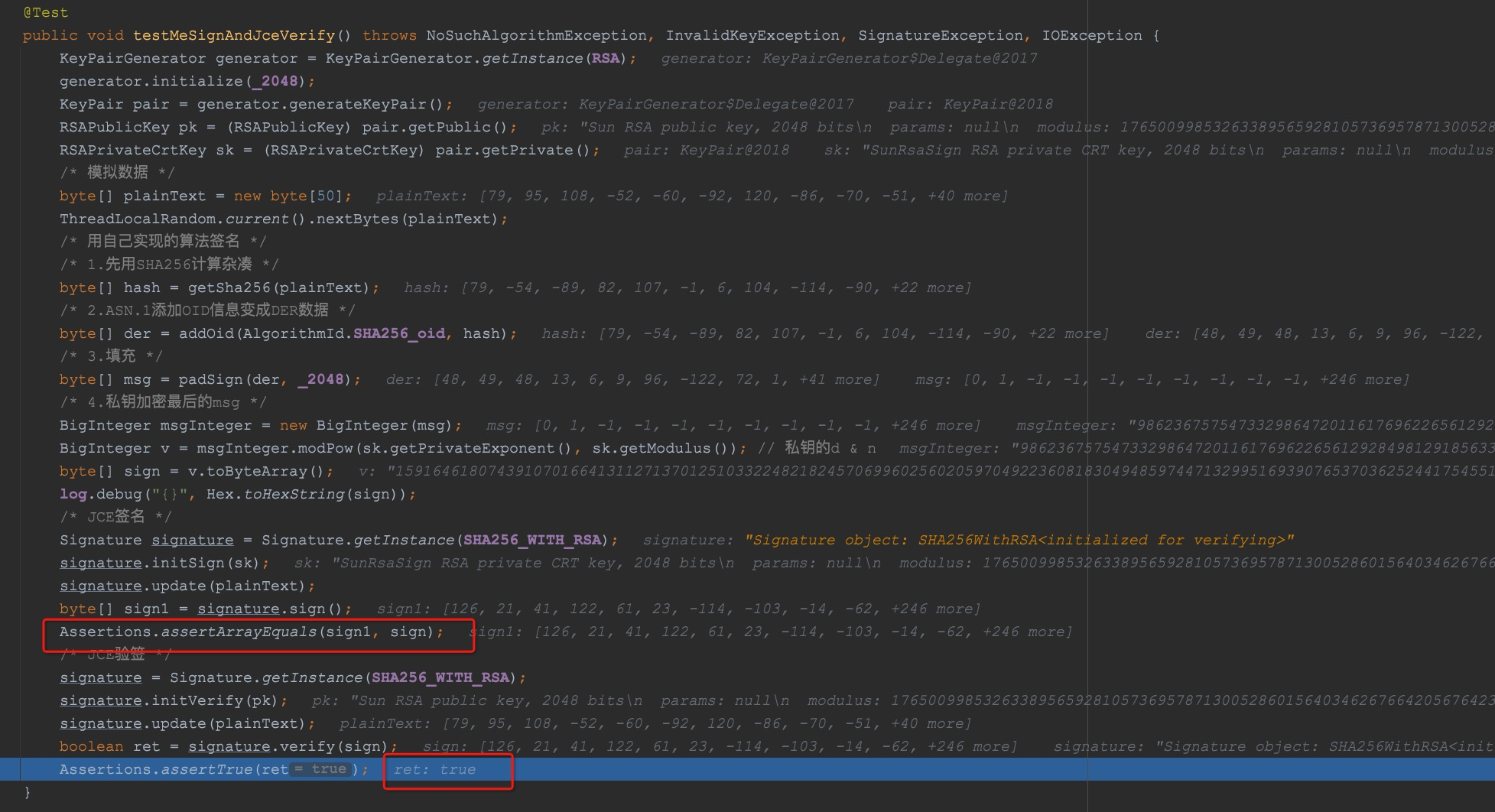
至此, RSA的签名算法也靠自己完全实现了,验签无非就是一个逆过程,读者可以自己去实践。

总结一下，签名值的长度肯定是和密钥长度完全一致，RSA2048就肯定是256字节，RSA1024就肯定是128字节,以此类推,由于签名填充使用0xFF，因此同样的数据使用同样的私钥签名，结果是一致的。这一点和加密不同。  

---

PS: 椭圆曲线的非对称算法和RSA完全不是一个体系,我会在另外一篇文章里说明。