2.4小时教你入门机器学习算法

2.4小时教你入门机器学习算法

现在很流行什么24小时精通xxx，我觉得24小时太久，不如试试2.4小时。
我会尝试用简单的说法解释复杂的事物。
人类一直在探索宇宙的真理，或者说探索宇宙的公式。周文王做《周易》也无非就是通过各种卦象推算出预言。再说直白一点，就是寻找y=f(x1,x2,x3,…)这样的公式。通过x1,x2,x3…去推导出结果y。

那么我私人定义一下机器学习的定义，通俗的说，就是让机器自己通过大量的样本（x1,y1）（x2,y2）…（xn,yn） (俗称大数据big data)，推导出这个f(x1,x2,x3)的公式。注意，机器学习只会根据样本推导出最接近真相的公式，但是不能回答为什么，不能解释原理。
即使你从未接触过机器学习，你肯定也知道这是一门非常复杂的学科。那么入门显然要从最简单的讲起，这篇文章不会教你调用什么API，这样就变成了调包侠，我们从最简单的原理讲起。
作为一个民间科学家，首先打开百度百科，搜索一下“方差公式”，可以看到以下信息：

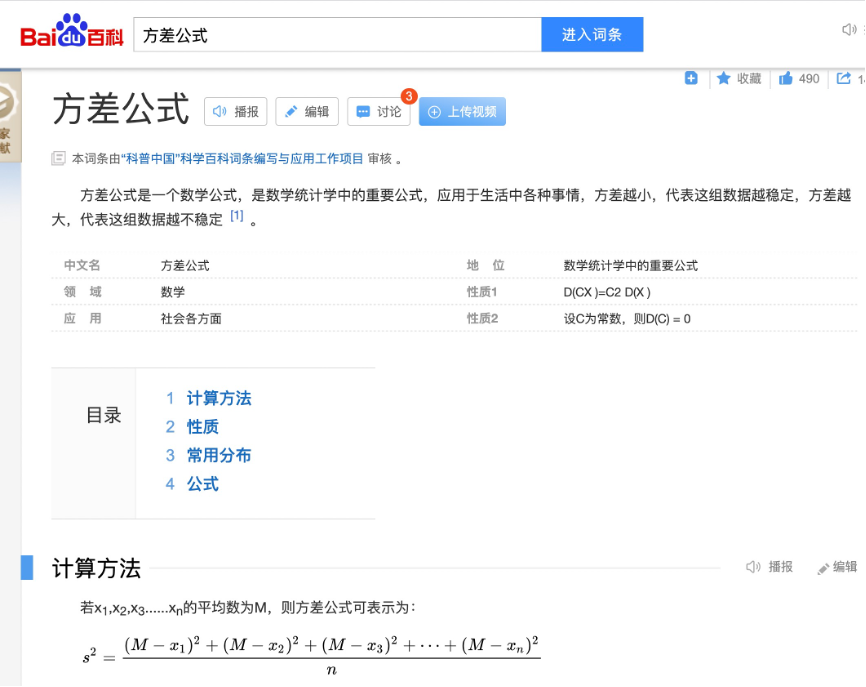
我们的故事就要从方差公式说起，即使上学期间是混日子的人都知道这个公式。事实上，我不能解释这个公式为什么这么定义，就当是大家公认的吧。这篇文章的例子都会遵循这个方差公式来定义稳定性。事实上，我们也可以自己定义自己的方差公式来定义自己系统的稳定性，在机器学习中，它的名字叫代价函数。
y=f(x1,x2,x3,…)是复杂的多维因子函数，作为入门教程，我们把它简化成只有一个输入因子的函数y=f(x)。我们的目的就是根据样本求出这个f()。
作为一个民间科学家，再打开百度百科，搜索一下“泰勒级数”

这里我来更加通俗的解释一下泰勒级数，我知道入门教程阅读者不会去学习太深的数学基础，所以我只会很直白的解释，说白了，泰勒就是想把任意的y=f(x)转换成好计算的多项式，本质就是把一条任意规律的线解释成多项式子的和。因为一条线想等同于另外一条线，只要他们在任意x点的导数相同，导数的导数相同，导数的导数的导数相同，导数的导数的导数的导数相同….那么他们就相同，因此我们可以把任意的y=f(x)分解成a*x^n + b*x^(n-1) + ……+ c*x^(1) + d 这样的多项式，问题就可以进一步简化。
作为入门教程，我们把难度收敛到多项式中最简单的一项：c*x^(1)，什么？你说d是最简单的一项？那好吧，那就收敛到第二简单的一项。也就是y=ax这样的一条直线。

也就是说任何复杂的公式，最终都是由若干的y= θx或者y= θx+b组成。从几何上来说，这就是一条直接，因此最简单的机器学习就是基于线性的回归。

干货：

假设我们拥有若干y=θx的样本，目的就是求出θ。那么我们就应该力求最一个θ使得样本的方差公式的结果最小，这样就最稳定，最符合样本的真相。注意，这很重要，这就是贯穿机器学习的核心方法论，让代价函数的值最小。

为了求出θ，我们定义一个关于θ的函数： z= J(θ).由此可知，这个函数应该是这样的：

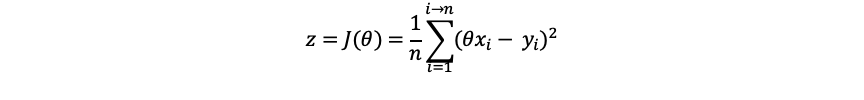
也就是方差公式。得到合适的θ值让z最小则成为了我们新的目标。
从习惯方便理解的方向，转换成对θ的公式。我们把这个公式转换习惯的y = f(x)公式。我们可以把x和y替换成a和b，把θ替换成x。想象成新的公式就应该是：

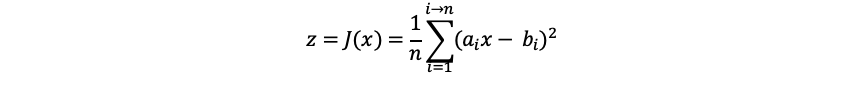
格式化写上面这个公式，费了我很多力气，所以接下来，还是让灵魂画手上场吧。

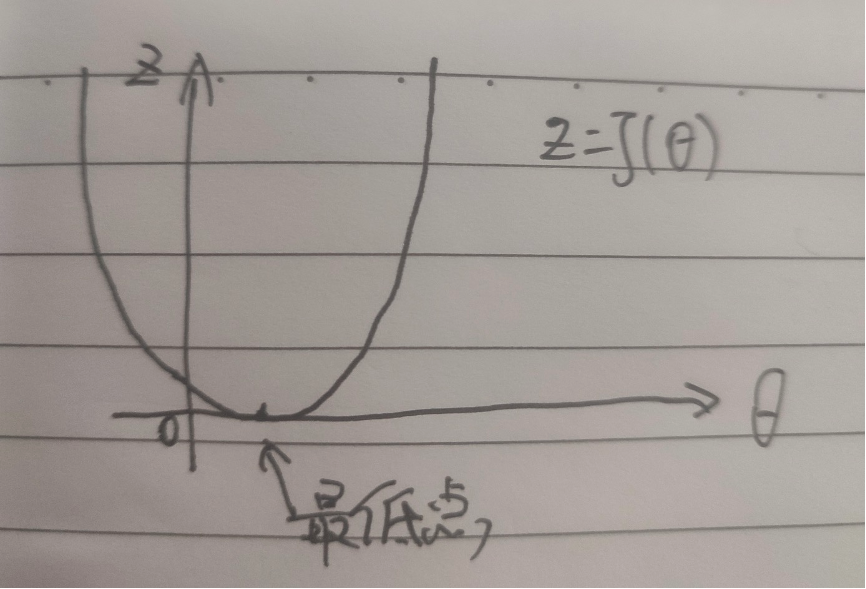
这个函数基本上是就是J(θ)的图形，嗯，一个U形（当变量变成2维之后，你可以想象就是一个立体的碗的形状，如果是3维就是，emo，我也想象不出来了），那么我们的目的就是要求出一个θ值让曲线的值最小最低。
有一个公式，可以让θ逐渐逼近最低点，这个过程，在机器学习中称为梯度下降法。假设我们初始设置θ值为0，然后让θ值变成θ值减去一个偏移，直到这个J(θ)的导数成为0，那么就找到了最低点。

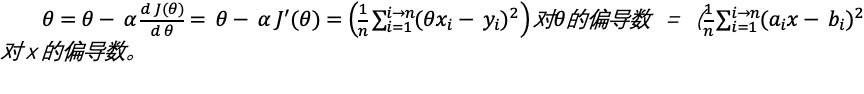
我们从下图来理解一下：

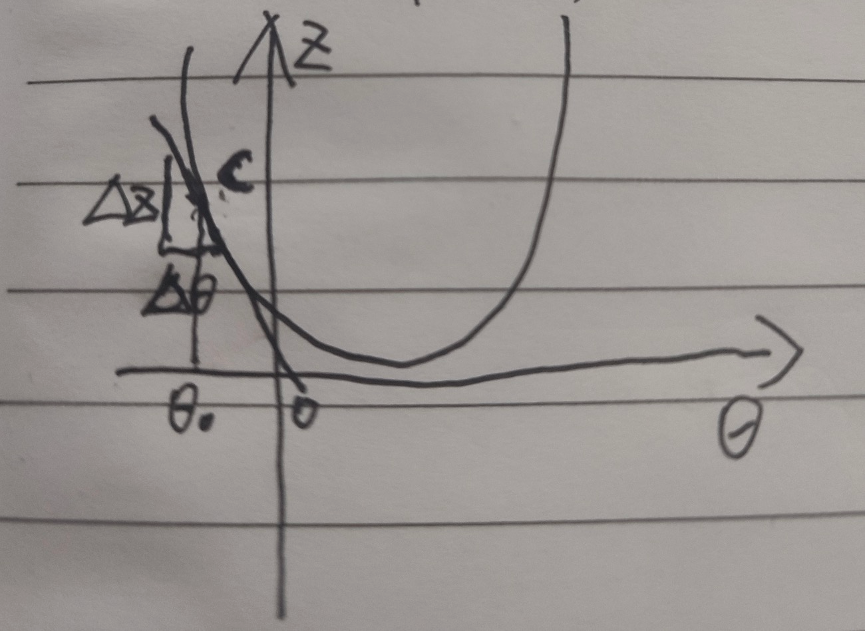
假设θ在最低值的左侧，对这个点求导数，也就是切线，可以得到一个很小的∆z和∆θ，事实上他们的比就是这个点的导数，那么这是一个负数，因此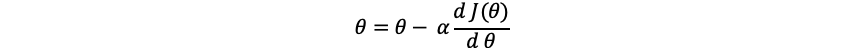就会让θ变大，然后右移，同理，我们取值在右侧，就会让θ变小，然后左移，当α比较小的时候，就会逐渐逼近最低点，直到导数为0 或者无限接近0的时候，就是最低点了。
上面我们得出那么也就是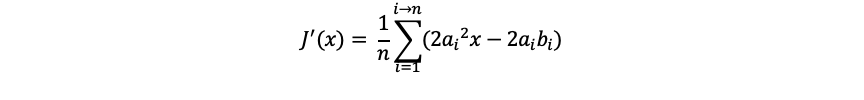

talk is cheap, show you the code.

首先我们定义一些点的用例case

@Data
@NoArgsConstructor
@AllArgsConstructor
public class Case {

    private double x;

    private double y;

    public static Case of(double x, double y) {
        return new Case(x, y);
    }
}

我们假定有一个y=f(x)的最简单的线性函数是y=θx,这里θ我们设置成一个随便设置的变量,可以得到原始函数

    private static final double REAL_SITA = 12.52D;

    /**
     * 原始函数
     *
     * @param x x值
     * @return y值
     */
    public double orgFunc(double x) {
        return REAL_SITA * x;
    }

然后构造1000个样本用例，并且假设用例不是很标准，有5%的误差，这样更加真实

    private static final int CASE_COUNT = 1000;
    private final List<Case> CASES = new ArrayList<>();
    
    /**
     * mock样本
    */
    private void makeCases() {
        List<Case> result = new ArrayList<>();
        for (int i = 0; i < CASE_COUNT; i++) {
            double x = ThreadLocalRandom.current().nextDouble(-100D, 100D);
            double y = orgFunc(x);
            boolean add = ThreadLocalRandom.current().nextBoolean();
            /* 为了仿真,y进行5%以内的抖动 */
            int percent = ThreadLocalRandom.current().nextInt(0, 5);
            double f = y * percent / 100;
            if (add) {
                y += f;
            } else {
                y -= f;
            }
            Case c = Case.of(x, y);
            result.add(c);
        }
        /* sort排序 */
        result.sort((o1, o2) -> {
            double v = o1.getX() - o2.getX();
            if (v < 0) {
                return -1;
            } else if (v == 0) {
                return 0;
            } else {
                return 1;
            }
        });
        this.CASES.clear();
        this.CASES.addAll(result);
    }

由于之前我们得到了求θ的导数公式，因此我们可以这样计算导数

    /**
     * J(θ)的导数
     *
     * @param sita θ
     * @return 导数值
     */
    public double derivativeOfJ (double sita) {
        double count = 0.0D;
        for (Case c : CASES) {
            double v = sita * c.getX() * c.getX() - c.getX() * c.getY();
            count += v;
        }
        return count / CASE_COUNT;
    }

最后我们设置一个小一点的α，然后假设 θ初始值为0，让 θ自己不停的去修正自己，得到最后的 θ值

    /**
     * J(θ)的导数
     *
     * @param sita θ
     * @return 导数值
     */
    public double derivativeOfJ (double sita) {
        double count = 0.0D;
        for (Case c : CASES) {
            double v = sita * c.getX() * c.getX() - c.getX() * c.getY();
            count += v;
        }
        return count / CASE_COUNT;
    }

    /**
     * 梯度下降
     */
    public double stepDownToGetSita() {
        double alpha = 0.0001D;
        /* 假设θ从0开始递增 */
        double sita = 0D;
        while (true) {
            double der = derivativeOfJ(sita);
            /* 由于计算机double有精度丢失，当导数der无限趋于0,则认为等于0 */
            if (Math.abs(der) < 0.000001) {
                return sita;
            }
            /* 不然就修正θ */
            sita -= alpha * der;
        }
    }

最后我们写一个junit来简单测试一下，看看能不能模糊计算出我们预先设置的θ值，和REAL_SITA比精度能到多少

    @Test
    public void test() {
        LineFunction lineFunction = new LineFunction();
        lineFunction.makeCases();
        double x = lineFunction.stepDownToGetSita();
        log.debug("x:{}", x);
    }

最后输出结果

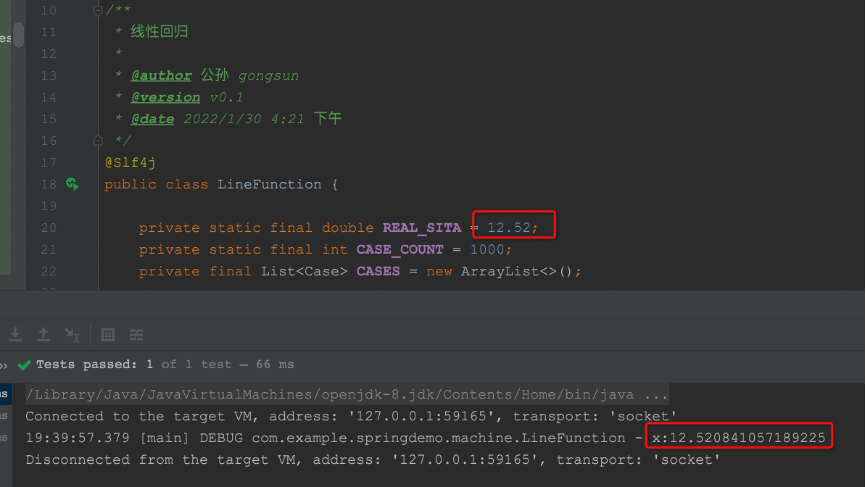
可见，预期值是12.52，我们计算出来是12.520841
什么？你说结果不是很精确？嗯，第一，这只是一个POC，第二，样本数量太少，第三，样本我进行了5%的模糊化，导致和本身的函数确实有误差。
嗯，机器学习的入门就是这样了，往后算子的复杂度会越来越高，但是原理就是这样。