图像的矩图像的轮廓面积和长度

1. 矩的概念

图像识别的一个核心问题是图像的特征提取，简单描述即为用一组简单的数据（图像描述量）来描述整个图像，这组数据越简单越有代表性越好。良好的特征不受光线、噪点、几何形变的干扰。图像识别发展几十年，不断有新的特征提出，而图像不变矩就是其中一个。

矩是概率与统计中的一个概念，是随机变量的一种数字特征。设 $X$

比较重要的有两种情况：

1. $c = 0$

2. $c = E (X)$

一阶原点矩就是期望。一阶中心矩 $μ_{1} = 0$

针对于一幅图像，我们把像素的坐标看成是一个二维随机变量 $(X, Y)$

不变矩(Invariant Moments)是一处高度浓缩的图像特征，具有平移、灰度、尺度、旋转不变性。M.K.Hu在1961年首先提出了不变矩的概念。1979年M.R.Teague根据正交多项式理论提出了Zernike矩。下面主要介绍这两种矩特征的算法原理与实现。

2. Hu矩

一幅 $M \times N$

m p q = \sum i = 1 M \sum j = 1 N i p j q f (i, j)

μ p q = \sum i = 1 M \sum j = 1 N (i - i ¯) p (j - j ¯) q f (

其中 $f (i, j)$

若将 $m_{00}$

$μ 00 = \sum_{i = 1}^{M} \sum_{j = 1}^{N} (i - \bar{i})^{0} (j - \bar{j})^{0} f (i, j) = m_{00}$

$μ 10 = \sum_{i = 1}^{M} \sum_{j = 1}^{N} (i - \bar{i})^{1} (j - \bar{j})^{0} f (i, j) = 0$

$μ 01 = \sum_{i = 1}^{M} \sum_{j = 1}^{N} (i - \bar{i})^{0} (j - \bar{j})^{1} f (i, j) = 0$

$μ 11 = \sum_{i = 1}^{M} \sum_{j = 1}^{N} (i - \bar{i})^{1} (j - \bar{j})^{1} f (i, j) = m_{11} - \bar{y} m_{10}$

$μ 20 = \sum_{i = 1}^{M} \sum_{j = 1}^{N} (i - \bar{i})^{2} (j - \bar{j})^{0} f (i, j) = m_{20} - \bar{y} m_{01}$

$μ 02 = \sum_{i = 1}^{M} \sum_{j = 1}^{N} (i - \bar{i})^{0} (j - \bar{j})^{2} f (i, j) = m_{02} - \bar{y} m_{01}$

$μ 30 = \sum_{i = 1}^{M} \sum_{j = 1}^{N} (i - \bar{i})^{3} (j - \bar{j})^{0} f (i, j) = m_{30} - 2 \bar{x} m_{20} + 2 {\bar{x}}^{2} m_{10}$

$μ 12 = \sum_{i = 1}^{M} \sum_{j = 1}^{N} (i - \bar{i})^{1} (j - \bar{j})^{2} f (i, j) = m_{12} - 2 \bar{y} m_{11} - \bar{x} m_{02} + 2 {\bar{y}}^{2} m_{10}$

$μ 21 = \sum_{i = 1}^{M} \sum_{j = 1}^{N} (i - \bar{i})^{2} (j - \bar{j})^{1} f (i, j) = m_{21} - 2 \bar{x} m_{11} - \bar{y} m_{20} + 2 {\bar{x}}^{2} m_{01}$

$μ 03 = \sum_{i = 1}^{M} \sum_{j = 1}^{N} (i - \bar{i})^{0} (j - \bar{j})^{3} f (i, j) = m_{03} - 2 \bar{y} m_{02} + 2 {\bar{y}}^{2} m_{01}$

为了消除图像比例变化带来的影响，定义规格化中心矩如下：

η p q = μ p a μ γ 00 , ( γ = p + q 2 , p + q = 2 , 3 , \dots )

利用二阶和三阶规格中心矩可以导出下面7个不变矩组 $(Φ_{1} Φ_{7})$

$Φ_{1} = η_{20} + η_{02}$

$Φ_{2} = (η_{20} - η_{02})^{2} + 4 η_{11}^{2}$

$Φ_{3} = (η_{20} - 3 η_{12})^{2} + 3 (η_{21} - η_{03})^{2}$

$Φ_{4} = (η_{30} + η_{12})^{2} + (η_{21} + η_{03})^{2}$

$Φ_{5} = (η_{30} + 3 η_{12}) (η_{30} + η_{12}) [(η_{30} + η_{12})^{2} - 3 (η_{21} + η_{03})^{2}] + (3 η_{21} - η_{03}) (η_{21} + η_{03}) [3 (η_{30} + η_{12})^{2} - (η_{21} + η_{03})^{2}]$

$Φ_{6} = (η_{20} - η_{02}) [(η_{30} + η_{12})^{2} - (η_{21} + η_{03})^{2}] + 4 η_{11} (η_{30} + η_{12}) (η_{21} + η_{03})$

$Φ_{7} = (3 η_{21} - η_{03}) (η_{30} + η_{12}) [(η_{30} + η_{12})^{2} - 3 (η_{21} + η_{03})^{2}] +] + (3 η_{12} - η_{30}) (η_{21} + η_{03}) [3 (η_{30} + η_{12})^{2} - (η_{21} + η_{03})^{2}]$

3. 利用OpenCV计算Hu矩

opencv里对Hu矩的计算有直接的API，它分为了两个函数：moments()函数用于计算中心矩，HuMoments函数用于由中心矩计算Hu矩。

Moments moments(InputArray array, bool binaryImage=false )

参数说明

输入参数：array是一幅单通道，8-bits的图像，或一个二维浮点数组(Point of Point2f)。binaryImage用来指示输出图像是否为一幅二值图像，如果是二值图像，则图像中所有非0像素看作为1进行计算。
输出参数：moments是一个类

4.contourArea()

contour:是一个向量，二维点，可以是vector或Mat类型

oriented:有默认值false，面向区域标识符，如果为true，该函数返回一个带符号的面积，其正负取决于轮廓的方向(顺时针还是逆时针)。根据这个特性可以根据面积的符号来确定轮廓的位置。如果是默认值false，则面积以绝对值的形式返回.

该函数使用Green formula计算轮廓面积，返回面积和非零像素数量如果使用drawContours或fillPoly绘制轮廓，可能导致不同。

5. arcLength()

用于计算封闭轮廓的周长或曲线的长度

curve:输入二维点集，可以是vector或Mat类型
closed:曲线是否封闭的标志位，true则封闭否则不封闭

 1 #include<opencv2/imgproc/imgproc.hpp>
 2 #include<opencv2/highgui/highgui.hpp>
 3 #include<iostream>
 4 
 5 using namespace cv;
 6 using namespace std;
 7 
 8 Mat src, grayImage;
 9 int Thresh = 100;
10 int MaxThresh = 255;
11 RNG rng(12345);
12 Mat canny_output;
13 vector<vector<Point>>contours;
14 vector<Vec4i>hierarchy;
15 
16 void on_threshChange(int, void *);
17  
18 int main()
19 {
20     src = imread("D:/meinv.jpg");
21 
22     cvtColor(src, grayImage, COLOR_BGR2GRAY);
23     blur(grayImage, grayImage, Size(3, 3));
24 
25     namedWindow("原图", CV_WINDOW_AUTOSIZE);
26     imshow("原图", src);
27 
28     //创建滚动条并进行初始化
29     createTrackbar("阈值", "原图", &Thresh, MaxThresh, on_threshChange);
30     on_threshChange(0, 0);
31     waitKey(0);
32     return(0);
33 }
34 
35 void on_threshChange(int, void*)
36 {   
37     //使用Canny检测边缘
38     Canny(grayImage, canny_output, Thresh, Thresh * 2, 3);
39     //找到轮廓
40     findContours(canny_output, contours, hierarchy, RETR_TREE, CHAIN_APPROX_SIMPLE, Point(0, 0));
41     //计算矩
42     vector<Moments>mu(contours.size());
43     for (int i = 0; i < contours.size(); i++)
44     {
45         mu[i] = moments(contours[i], false);
46     }
47     //计算图像的质心
48     vector<Point2f>mc(contours.size());
49     for (int i = 0; i < contours.size(); i++)
50     {
51         mc[i] = Point2f(static_cast<float>(mu[i].m10 / mu[i].m00), static_cast<float>(mu[i].m01 / mu[i].m00));
52     }
53     //绘制轮廓
54     Mat drawing = Mat::zeros(canny_output.size(), CV_8UC3);
55     for (int i = 0; i < contours.size(); i++)
56     {
57         Scalar color = Scalar(rng.uniform(0, 255), rng.uniform(0, 255), rng.uniform(0, 255));
58         drawContours(drawing, contours, i, color, 2, 8, hierarchy, 0, Point());
59         circle(drawing, mc[i], 4, color, -1, 8, 0);
60     }
61     //显示到窗口中
62     namedWindow("轮廓图", WINDOW_AUTOSIZE);
63     imshow("轮廓图", drawing);
64 
65     //用moments矩集计算轮廓面积并与opencv函数计算结果进行比较
66     printf("\t Info: Area and Contour Length \n");
67     for (int i = 0; i < contours.size(); i++)
68     {
69         printf("* Contour[%d] - Area(M_00)=%.2f-Area OpenCV:%.2f - Length:%.2f\n", i, mu[i].m00, contourArea(contours[i]), arcLength(contours[i], true));
70         Scalar color = Scalar(rng.uniform(0, 255), rng.uniform(0, 255), rng.uniform(0, 255));
71         drawContours(drawing, contours, i, color, 2, 8, hierarchy, 0, Point());
72         circle(drawing, mc[i], 4, color, -1, 8, 0);
73     }
74 }

效果图：

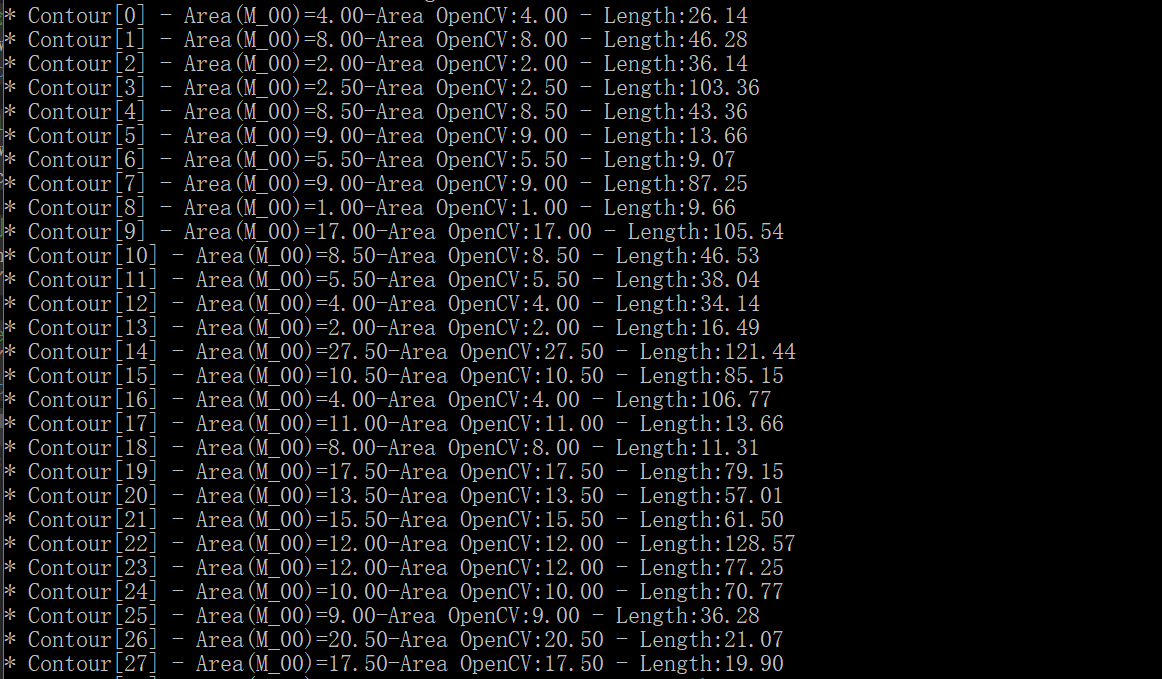
本文参考自：https://blog.csdn.net/keith_bb/article/details/70197104

　　　　　　http://www.cnblogs.com/ronny/p/3985810.html

posted @ 2018-09-29 19:31 RamboBai 阅读(1436) 评论(0) 编辑收藏举报

刷新页面返回顶部

有理想

图像的矩图像的轮廓面积和长度

1. 矩的概念

2. Hu矩

3. 利用OpenCV计算Hu矩

参数说明

4.contourArea()

5. arcLength()

公告

有理想

图像的矩 图像的轮廓面积和长度

1. 矩的概念

2. Hu矩

3. 利用OpenCV计算Hu矩

参数说明

4.contourArea()

5. arcLength()

公告

图像的矩图像的轮廓面积和长度