OO第一次总结
OO第一次总结
一、架构设计体验
本次作业的主要目的是实现一个支持求和函数sum(i,s,e,expr),自定义函数f(x,y,z),以及三角函数及各种因子的表达式进行拆括号、化简工作。要求最终结果复合表达式定义,且没有多余括号。
对于该问题,我将按照课上所示输入处理(Parser...)、主控(Arith....)、核心数据管理(Expr)三个板块进行说明。
输入处理
首先是输入处理部分,采用递归下降的思路解析字符串,依据工厂模式设计相应的Factory完成类的创建。实现了高内聚低耦合的思想。
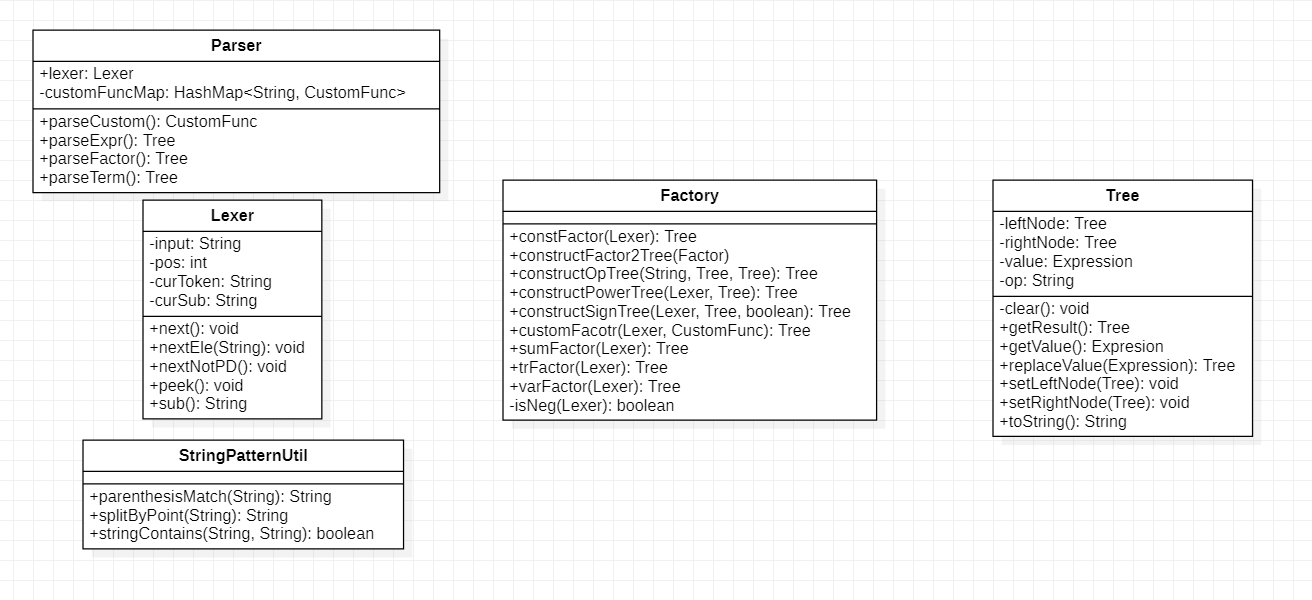
整个解析字符串的流程是:
- 根据输入
String创建相应的Lexer和Parser。 Parser对字符串内容进行递归下降解析,StringPatternUtil类提供工具支持,判断当前层次属于哪一个数据管理类。- 根据当前的不同层次,把字符串交给
Factory进行相应的解析与创建。 Tree作为创建好的,Operator以及Expression的容器,并负责与下一步主控以及数据管理部分进行交互。
流程控制
其次是主要的流程控制阶段,流程控制主要是针对根据递归下降所创建的Tree进行递归求解的操作。
这个过程主要涉及表达式之间的加、减、乘、乘方等操作。
- 对于加法,我们希望两个表达式进行加法化简,并返回一个新的表达式。
- 对于减法,我们将其化为对于减数的相反数的加法的操作。
- 对于乘法,我们将其化简为,拆分表达式中每一个
TermInterface层次,进行分配律化简。 - 对于乘方,我们将其化简为,多个表达式相乘,并调用乘法的方法。
这样看来,对于表达式的化简过程仍然具有很强的层次性,因此据此设计一个相应的数据管理结构便尤为重要。
数据管理结构
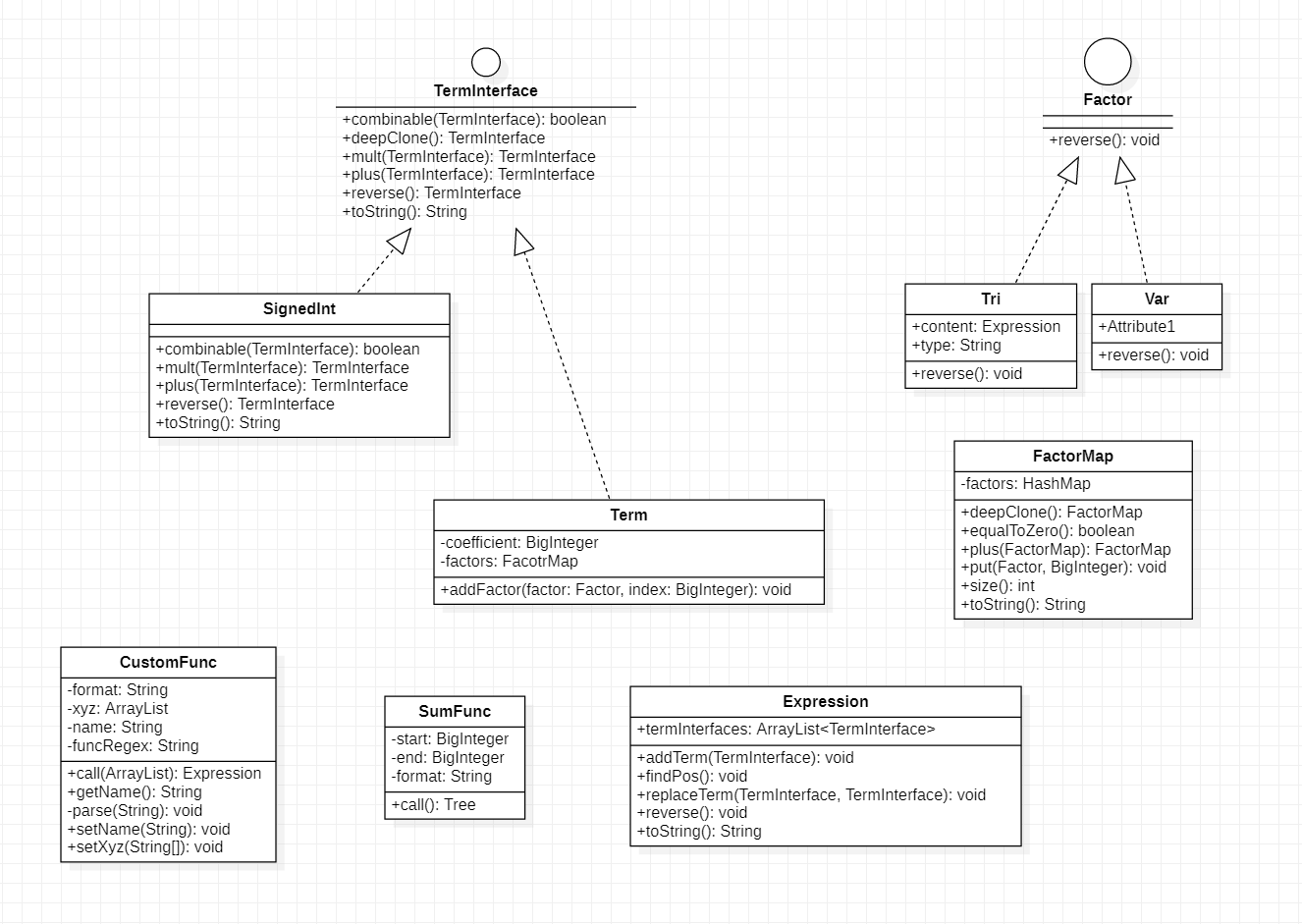
对于数据管理结构部分,我们将其分解为三个层次,因子,项,表达式。并依据这三个层次结构,构建相应的实体类。

对于因子层次,虽然要求中说明有三角函数、幂函数、和表达式因子三种。但本文对于因子的设计思路有偏,既不保存表达式因子。所以实际上,只有三角函数和幂函数两种。表达式交由结果树进行运算时展开处理。
对于项层次,为了实现这一层次的一些共性,选择将常数、以及Term继承TermInterface接口实现以下函数:
- combinable(TermInterface): 判断传入参数与自身是否可以加法层次合并
- mult(TermInterface): 返回传入参数与自身乘法的结果。
- plus(TermInterface): 返回传入参数与自身加法的结果。
- reverse(): 返回自身相反数
实现以上接口函数,便可以完成Term层次的所有操作。实现加法,乘法等等。同时Term以因子为变量,储存每一个term变量。通过实现一个HashMap,以因子作为键,幂作为值。保存相应的因子,并重写一部分HashMap函数。创建符合要求的FactorMap。
对于表达式层次,我们用一个ArrayList储存其中的每一个TermInterface,并实现特有的
- addTerm(TermInterface): 增加
Term。 - findPos(): 寻找第一个非负项。
- replace(TermInterface, TermInterface):替代
- reverse(): 返回相反表达式
这样,我们的表达式就能和其他表达式参与运算,化简等工作。
最后再叙述一下,自定义函数因子和求和函数因子。对于这两个因子,我采用了较为简单的替换字符串的形式。并实现统一的接口call完成函数的调用。首先根据具体结构创建相应函数类,然后再设置相应自变量与参数—(x,y,z,i)等等,最后调用call返回相应的运算树。
二、问题、bug、共性问题分析探讨
针对三次作业,我想阐述以下几个方面的一些共性问题和bug。
- 对于第一次作业而言,我在处理输入表达式时,因为读题不仔细,致使对于空白符的判断出现问题。因此出现了第一个较为严重的bug:对多个空白符解析失败。而出现这个bug的原因我认为是由于我的解析方针。以大方向梯度下降,配合局部正则表达式匹配来完成。这导致正则表达式部分稍微复杂,容易出错。

为此我在之后的作业中,特地优化了正则表达式,并在在线测试平台上多加测试。完善了这一问题。同时这一个问题也并非我个人,和我处于同一房间的一位同学也犯了相同的错误,并在互测中暴露出来。
-
对于第二次作业,由于加入了新求和函数和自定义函数。我对其进行了字符串替换处理而在这个过程中出现了如下问题。首先是:\(i^{2}, i=-1\)对于这种数据,在数学意义上,应当是\(-(1)^{2}\),而在字符串替换过程中,容易错误生成\(-1^{2}\)致使结果出错。
同样的问题还有对三角函数化简的过程中,我将\(sin\)中的负号提出。如\(sin(-1)^{2}=(-sin(1))^{2}\),但在替换过程中,也是由于考虑不周,替换为了\(sin(-1)^{2}=-sin(1)^2\)导致错误。究其根本,是由于对于其背后的数学本质考虑不周。产生此类错误。因此以先建立运算树,再替换的方式,将避免此类错误的出现。这个问题也是普遍存在的一个问题。这出现bug部分的函数为
parse.Factory.triFactor(Lexer)这一部分的复杂度相对较高,原因是在此处处理了三角函数内的负号,但也导致了出现该问题。因此,对于复杂度较高,且非结构化程度高的代码,其出bug的可能性还是非常之大的! -
对于第三次作业,支持函数嵌套功能。因此需要对求和函数与自定义函数的解析部分重构。再这个过程中,由于之前使用的
String.split方法不兼容,导致多层嵌套的解析出错。需要自己实现一个类似功能,并能将变量看作整体的新函数。
同时hack他人的程序部分,我虽然没有精打细算的去读取别人的代码。因为于我而言,阅读他人代码,理解他人思路是一个很痛苦的过程。大家各自有各自处理自己字符串的思路。因此我采用了单元测试+盲试的方法。
首先是用自己构建的,带有部分坑点,以及边缘条件的测试样例去测试。若找到了bug,再对测试样例中相应坑点部分进行单元测试,以防多个测试样例hack到相同bug的情况。
这样的思路虽然低效,但却是去理解其余7个人的代码,并且还不一定能找到bug的情况下对我而言的最好选择。
三、度量分析
Class
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| MainClass | 2 | 2 | 2 |
| arithtool.Arith | 3.25 | 5 | 13 |
| exp.CustomFunc | 1.33 | 2 | 8 |
| exp.Expression | 2 | 4 | 26 |
| exp.FactorMap | 2.44 | 5 | 22 |
| exp.SignedInt | 1.22 | 2 | 11 |
| exp.SumFunc | 1.5 | 2 | 3 |
| exp.Term | 1.92 | 5 | 25 |
| exp.Tree | 2.8 | 9 | 28 |
| exp.Tri | 1.38 | 3 | 11 |
| exp.Var | 1.25 | 3 | 10 |
| parse.Factory | 2.27 | 8 | 25 |
| parse.Lexer | 2.7 | 6 | 27 |
| parse.Parser | 2.25 | 9 | 27 |
| parse.StringPatternUtil | 3 | 4 | 9 |
| Total | 247.0 | ||
| Average | 2.07 | 4.6 | 16.46 |
上图为类的复杂度分析,可以看出大多数类的复杂度较低,只有部分承担核心工作的类,内部聚合度较高,对于不同的类,针对特定功能实现高内聚的一个思想。例如其中:
-
Arith类专门负责进行运算树的拆分化简工作。
-
Parser类负责字符串的解析。
-
Factory类负责根据解析结果创建相应的运算树。
等等..。
Method
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| MainClass.main(String[]) | 1 | 1 | 2 | 2 |
| arithtool.Arith.multiply(Expression, Expression) | 7 | 1 | 5 | 5 |
| arithtool.Arith.plus(Expression, Expression) | 0 | 1 | 1 | 1 |
| arithtool.Arith.power(Expression, TermInterface) | 2 | 2 | 3 | 3 |
| arithtool.Arith.termPlus(Expression, ArrayList |
13 | 4 | 6 | 6 |
| exp.CustomFunc.CustomFunc(String) | 0 | 1 | 1 | 1 |
| exp.CustomFunc.call(ArrayList |
1 | 1 | 2 | 2 |
| exp.CustomFunc.getName() | 0 | 1 | 1 | 1 |
| exp.CustomFunc.parse(String) | 1 | 1 | 2 | 2 |
| exp.CustomFunc.setName(String) | 0 | 1 | 1 | 1 |
| exp.CustomFunc.setXyz(String[]) | 0 | 1 | 1 | 1 |
| exp.Expression.Expression() | 0 | 1 | 1 | 1 |
| exp.Expression.addTerm(TermInterface) | 0 | 1 | 1 | 1 |
| exp.Expression.deepClone() | 1 | 1 | 2 | 2 |
| exp.Expression.equals(Object) | 3 | 3 | 2 | 4 |
| exp.Expression.findPos() | 3 | 3 | 2 | 3 |
| exp.Expression.getTerms() | 0 | 1 | 1 | 1 |
| exp.Expression.hashCode() | 0 | 1 | 1 | 1 |
| exp.Expression.isAllNeg() | 3 | 3 | 2 | 3 |
| exp.Expression.isExpr() | 2 | 1 | 5 | 5 |
| exp.Expression.replaceTerm(TermInterface, TermInterface) | 4 | 1 | 3 | 3 |
| exp.Expression.reverse() | 1 | 1 | 2 | 2 |
| exp.Expression.simplify() | 0 | 1 | 1 | 1 |
| exp.Expression.toString() | 5 | 1 | 3 | 4 |
| exp.FactorMap.FactorMap() | 0 | 1 | 1 | 1 |
| exp.FactorMap.deepClone() | 1 | 1 | 2 | 2 |
| exp.FactorMap.equalToZero() | 3 | 3 | 2 | 3 |
| exp.FactorMap.equals(Object) | 3 | 3 | 2 | 4 |
| exp.FactorMap.hashCode() | 0 | 1 | 1 | 1 |
| exp.FactorMap.plus(FactorMap) | 7 | 1 | 5 | 5 |
| exp.FactorMap.put(Factor, BigInteger) | 0 | 1 | 1 | 1 |
| exp.FactorMap.size() | 0 | 1 | 1 | 1 |
| exp.FactorMap.toString() | 7 | 1 | 5 | 5 |
| exp.SignedInt.SignedInt(String) | 0 | 1 | 1 | 1 |
| exp.SignedInt.combinable(TermInterface) | 3 | 2 | 3 | 3 |
| exp.SignedInt.deepClone() | 0 | 1 | 1 | 1 |
| exp.SignedInt.getCoefficient() | 0 | 1 | 1 | 1 |
| exp.SignedInt.getFactors() | 0 | 1 | 1 | 1 |
| exp.SignedInt.mult(TermInterface) | 0 | 1 | 1 | 1 |
| exp.SignedInt.plus(TermInterface) | 1 | 2 | 2 | 2 |
| exp.SignedInt.reverse() | 0 | 1 | 1 | 1 |
| exp.SignedInt.toString() | 0 | 1 | 1 | 1 |
| exp.SumFunc.SumFunc(BigInteger, BigInteger, String) | 0 | 1 | 1 | 1 |
| exp.SumFunc.call() | 1 | 1 | 2 | 2 |
| exp.Term.Term(BigInteger) | 0 | 1 | 1 | 1 |
| exp.Term.addFactor(Factor, BigInteger) | 1 | 1 | 2 | 2 |
| exp.Term.combinable(TermInterface) | 3 | 2 | 3 | 3 |
| exp.Term.deepClone() | 0 | 1 | 1 | 1 |
| exp.Term.equals(Object) | 4 | 3 | 3 | 5 |
| exp.Term.getCoefficient() | 0 | 1 | 1 | 1 |
| exp.Term.getFactors() | 0 | 1 | 1 | 1 |
| exp.Term.hashCode() | 0 | 1 | 1 | 1 |
| exp.Term.mult(TermInterface) | 2 | 2 | 2 | 2 |
| exp.Term.plus(TermInterface) | 7 | 5 | 5 | 5 |
| exp.Term.reverse() | 0 | 1 | 1 | 1 |
| exp.Term.setFactors(FactorMap) | 0 | 1 | 1 | 1 |
| exp.Term.toString() | 6 | 1 | 4 | 4 |
| exp.Tree.Tree(Expression) | 0 | 1 | 1 | 1 |
| exp.Tree.Tree(String) | 0 | 1 | 1 | 1 |
| exp.Tree.clear() | 0 | 1 | 1 | 1 |
| exp.Tree.getResult() | 6 | 6 | 6 | 6 |
| exp.Tree.getValue() | 0 | 1 | 1 | 1 |
| exp.Tree.replaceValueI(Expression) | 7 | 1 | 3 | 6 |
| exp.Tree.replaceValueXyz(Expression, Expression, Expression) | 7 | 1 | 3 | 8 |
| exp.Tree.setLeftNode(Tree) | 0 | 1 | 1 | 1 |
| exp.Tree.setRightNode(Tree) | 0 | 1 | 1 | 1 |
| exp.Tree.toString() | 0 | 1 | 1 | 1 |
| exp.Tri.Tri(Expression, String) | 0 | 1 | 1 | 1 |
| exp.Tri.deepClone() | 0 | 1 | 1 | 1 |
| exp.Tri.equals(Object) | 4 | 3 | 3 | 5 |
| exp.Tri.getContent() | 0 | 1 | 1 | 1 |
| exp.Tri.getType() | 0 | 1 | 1 | 1 |
| exp.Tri.hashCode() | 0 | 1 | 1 | 1 |
| exp.Tri.reverse() | 0 | 1 | 1 | 1 |
| exp.Tri.toString() | 1 | 1 | 1 | 2 |
| exp.Var.Var(String) | 0 | 1 | 1 | 1 |
| exp.Var.deepClone() | 0 | 1 | 1 | 1 |
| exp.Var.equals(Object) | 3 | 3 | 2 | 4 |
| exp.Var.getType() | 0 | 1 | 1 | 1 |
| exp.Var.hashCode() | 0 | 1 | 1 | 1 |
| exp.Var.reverse() | 0 | 1 | 1 | 1 |
| exp.Var.setType(String) | 0 | 1 | 1 | 1 |
| exp.Var.toString() | 0 | 1 | 1 | 1 |
| parse.Factory.constFactor(Lexer) | 1 | 1 | 2 | 2 |
| parse.Factory.constructFactor2Tree(Factor) | 0 | 1 | 1 | 1 |
| parse.Factory.constructOpTree(String, Tree, Tree) | 0 | 1 | 1 | 1 |
| parse.Factory.constructPowerTree(Lexer, Tree) | 3 | 1 | 3 | 3 |
| parse.Factory.constructSignTree(Lexer, Tree, boolean) | 1 | 1 | 2 | 2 |
| parse.Factory.customFactor(Lexer, CustomFunc) | 0 | 1 | 1 | 1 |
| parse.Factory.isNeg(Lexer) | 1 | 1 | 2 | 2 |
| parse.Factory.sumFactor(Lexer) | 0 | 1 | 1 | 1 |
| parse.Factory.toVarIndex(String) | 2 | 1 | 1 | 2 |
| parse.Factory.triFactor(Lexer) | 9 | 1 | 8 | 8 |
| parse.Factory.varFactor(Lexer) | 1 | 1 | 2 | 2 |
| parse.Lexer.Lexer(String) | 0 | 1 | 1 | 1 |
| parse.Lexer.getNumber() | 2 | 1 | 3 | 3 |
| parse.Lexer.next() | 7 | 6 | 6 | 6 |
| parse.Lexer.nextEle(String) | 5 | 5 | 5 | 5 |
| parse.Lexer.nextNotEmpty() | 4 | 4 | 4 | 4 |
| parse.Lexer.nextNotPD() | 4 | 4 | 4 | 4 |
| parse.Lexer.peek() | 0 | 1 | 1 | 1 |
| parse.Lexer.sub() | 0 | 1 | 1 | 1 |
| parse.Lexer.toString() | 0 | 1 | 1 | 1 |
| parse.Lexer.update() | 2 | 1 | 2 | 2 |
| parse.Parser.Parser(Lexer) | 0 | 1 | 1 | 1 |
| parse.Parser.isConst() | 0 | 1 | 1 | 1 |
| parse.Parser.isCustomF() | 0 | 1 | 1 | 1 |
| parse.Parser.isExpr() | 0 | 1 | 1 | 1 |
| parse.Parser.isSum() | 0 | 1 | 1 | 1 |
| parse.Parser.isTri() | 0 | 1 | 1 | 1 |
| parse.Parser.isVar() | 0 | 1 | 1 | 1 |
| parse.Parser.parseCustom() | 0 | 1 | 1 | 1 |
| parse.Parser.parseExpr() | 5 | 4 | 3 | 5 |
| parse.Parser.parseFactor() | 10 | 7 | 9 | 9 |
| parse.Parser.parseTerm() | 4 | 4 | 2 | 4 |
| parse.Parser.setCustomFunc(HashMap<String, CustomFunc>) | 0 | 1 | 1 | 1 |
| parse.StringPatternUtil.parenthesisMatch(String) | 4 | 1 | 3 | 4 |
| parse.StringPatternUtil.splitByPoint(String) | 5 | 1 | 4 | 4 |
| parse.StringPatternUtil.stringContains(String, String) | 0 | 1 | 1 | 1 |
| Total | 194.0 | 179.0 | 233.0 | 262.0 |
| Average | 1.63 | 1.50 | 1.95 | 2.20 |
在方法度量部分,可以看出大部分方法的复杂度都是较低的。除了部分内容较为复杂,例如
Parser.parseFactor需要处理五大因子,并调用相应创建函数。Arith.termPlus需要判断是否能加法合并,以及一系列条件以外。
除开部分功能设定复杂的方法模块外。其余方法的复杂度都较低。
同时进一步分析,非结构化程度\(ev(G)=1.50\)说明代码的平均基本复杂度较低,大部分方法并未出现较高的非复杂度,为代码的维护创造困难。
而\(Iv(G)=1.95\)同样不超过2,说明模块设计之间的耦合度不高,隔离度较好。有利于代码的复用以及单元测试等等。
而\(v(G)=2.20\)圈复杂度大于模块设计复杂度,但也并非远远超出。这对于代码测试的路径是一个非常好的帮助。
四、本单元学习的心得体会
本单元的重点,我认为是体会java的编程范式,以及及其重要的层次化思想。
层次化思想我认为是java面向对象非常重要的一步,而OO课程组选择用解析表达式的方式来让我们取体会这其中的奥妙也是十分有效的。
通过这次作业,我能对于不同类,即此处的表达式、因子、项之间复杂的嵌套耦合关系有一个初步的认知。一个表达式它既承载着初始的表达式形式,又可以作为因子参与因子层次的运算等等。这种错综复杂的关系,需要我们提炼其本质,将其转换为运算的层次关系,并提炼出相应的共性方法去设计相应的接口来完成描述一个表达式所需要的方方面面。
这也让我明白了先画UML图,再进行相应的类构建也是十分有效的手段。能有助于自己理清楚层次结构关系,减少coding时的重构可能性。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号