codeforces#1293E. Xenon's Attack on the Gangs(树上dp)

 

题目链接：

https://codeforces.com/contest/1293/problem/E

题意：

给出一颗节点数为$n$的树，可以给它的每条边赋从$0$到$n-1$的值，不能重复赋值

定义$mex(u,v)$为从节点$u$到$v$的最短路径中没有出现的权值的最小整数

计算下面等式的最大值：

$$S = \sum_{1 \leq u < v \leq n} mex(u, v)$$

分析：

根据以下等式：

$$S = \sum_{1 \leq u < v \leq n} mex(u, v) = \sum_{1 \leq x \leq n} \left( \sum_{mex(u, v) = x} x \right) = \sum_{1 \leq x \leq n} \left( \sum_{mex(u, v) \geq x} 1 \right) = \sum_{1 \leq x \leq n} f(x)$$

我们只需要依次计算$f(x)$即可，$f(x)$为路径上包括权值$0$到$x-1$的节点对数

 定义$dp[u][v]$为，假设$u$到$v$的长度为$l$，把$0$到$l-1$都填充入$u$到$v$的路径的最大值，不计算$l$到$n-1$权值的贡献

 显然，$l-1$只有两种填充情况，在$u$附近或者$v$附近

 

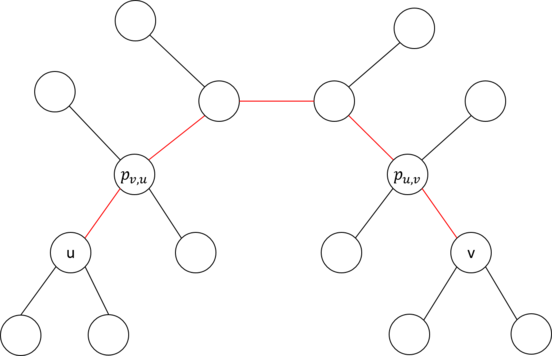
 定义$sub(u,v)$为，以$u$为根节点时，$v$的子树大小

 定义$par(u,v)$为，以$u$为根节点时，$v$的父节点

 $$dp[u][v] = sub(u, v) \times sub(v, u) + \max(dp[par(v, u)][v], dp[u][par(u, v)])$$

 AC代码：

#include <bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for (int i=a;i<=b;i++)
#define per(i,a,b) for (int i=b;i>=a;i--)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define SZ(x) ((int)(x).size())

typedef long long ll;
typedef vector<int> VI;
typedef pair<int,int> PII;

const ll mod=1e5+7;
const int maxn=3e3+7;

ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}

VI ve[maxn];
int par[maxn][maxn],sub[maxn][maxn];
int root,n;
ll dp[maxn][maxn];
void dfs(int x,int fa){
    par[root][x]=fa;
    sub[root][x]=1;
    for(auto i:ve[x]){
        if(i==fa)continue;
        dfs(i,x);
        sub[root][x]+=sub[root][i];
    }
}
ll getdp(int u,int v){
    if(u>v)swap(u,v);
    if(dp[u][v]!=-1)return dp[u][v];
    if(u==v)return 0;
    dp[u][v]=max(getdp(u,par[u][v]),getdp(v,par[v][u]))+sub[u][v]*sub[v][u];
    return dp[u][v];
}
int main() {
    scanf("%d",&n);
    rep(i,1,n-1){
        int a,b;
        scanf("%d %d",&a,&b);
        ve[a].pb(b);
        ve[b].pb(a);
    }
    rep(i,1,n){
        root=i;
        dfs(i,-1);
    }
    memset(dp,-1,sizeof(dp));
    ll ans=0;
    rep(i,1,n){
        rep(j,i+1,n){
            ans=max(ans,getdp(i,j));
        }
    }
    printf("%lld\n",ans);
    return 0;
}