P3403 跳楼机

题意：给定h,x,y,z，求由x,y,z组成的数中有多少个小于等于h。

解：学习同余最短路的例题。由于h太大(h<=(1<<63)-1)，考虑找规律。首先xyz中有任何一个为1答案为h。否则，将xyz能组成的数按照模x同余分类，于是现在只需要考虑y和z。为了和模运算一致，将h减一，求0~h-1中答案的个数。

用一个例子来说明：h=46, x=4,y=7,z=9

x的剩余系：                            0    1    2    3

模x同余的最小数（d_i）：       0    9   14   7

将h按照每x个数分一组，将 x的倍数+模x同余的最小数 填入：

如此计算一下，就有了oiwiki上的那个式子：

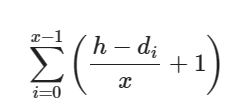
代码：

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define maxx 300005
#define inf (1ull<<63)-1
#define int long long
ll h,x,y,z;
struct edge{
    int u,v,w;
    int nxt;
}e[maxx];
int head[maxx]={0},cnt=0;
void add(int u,int v,int w){
    e[++cnt].u=u;
    e[cnt].v=v;
    e[cnt].w=w;
    e[cnt].nxt=head[u];
    head[u]=cnt;
}
ll dis[maxx];
int vis[maxx]={0};
void dijk(){
    for(int i=0;i<x;i++) dis[i]=inf;
    dis[0]=0;
    priority_queue<pair<int,int> > q;
    q.push(make_pair(0,0));
    while(!q.empty()){
        int now=q.top().second;
        q.pop();
        if(vis[now]) continue;
        vis[now]=1;
        for(int i=head[now];i;i=e[i].nxt){
            int to=e[i].v;
            ll f=e[i].w+dis[now];
            if(f<dis[to]){
                dis[to]=f;
                q.push(make_pair(-dis[to],to));
            }
        }
    }
}
signed main(){
    scanf("%lld%lld%lld%lld",&h,&x,&y,&z);
    if(x==1||y==1||z==1){
        printf("%lld\n",h);
        return 0;
    }
    for(int i=0;i<x;i++){
        add(i,(i+y)%x,y);
        add(i,(i+z)%x,z);
    }
    dijk();
    h--;
    ll ans=0;
    for(int i=0;i<x;i++){
        if(h>=dis[i]) ans+=(h-dis[i])/x+1;
    }
    printf("%lld\n",ans);
}