词法分析及词法分析程序
本章所用文法为3型文法，即左线性文法或右线性文法。目标是识别出程序中的变量，符号，立即数，关键字等你想识别的东西，为后续文法分析作准备。主要过程为建立识别单词符号（token）的自动机，然后把语句扔进去跑。
单词符号有多种表达方式，我们通过分析其生成方式来识别它们。书中介绍了状态转换图，文法和正则式，以及它们之间的互相转化。
1. 状态转换图与文法
书中只介绍左/右线性文法转化到自动机，如果不是右线性文法，应该先要转化为右线性，转化过程主要靠意会这种语言讲了什么。
接下来是右线性文法转化自动机的过程：
对于A→aB，就是画一个A到B的箭头，上面写a。对于A→a，画一个A到终结结点的箭头，上面写a。对于A→ε，从A画一个到终结结点的箭头。
对于左线性文法，箭头方向相反即可。
文法转状态转换图亦然。
2. 状态转换图与正则式
正则式有三种符号：| 表示或，· 表示连在后面，* 表示闭包。
(a | b)*a: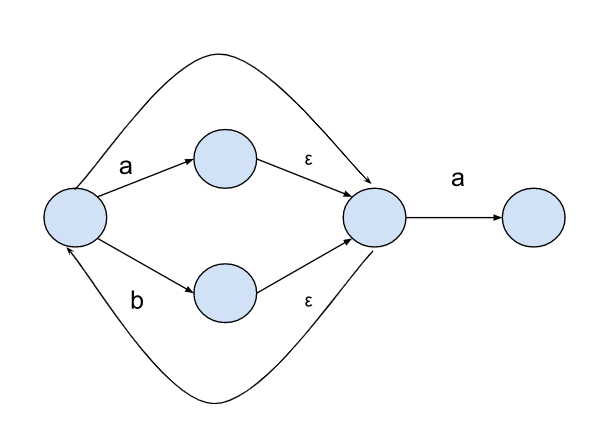 
反之亦然。
3. 文法与正则式
中间画个转化图辅助一下，或者直接意会（
现在考虑推广状态转换图，做一个自动机。
定义DFA（deterministic finite automaton）为，有限个字符，有限个状态，加入一个新的元素能确定转换到哪个状态，且只有一个初态。
定义NFA（nondeterministic finite automaton），就是加入一个新的元素有多个后继可以选择，并不能决定（determine）进入哪个状态。相应地，它有多个初态。
4. NFA确定化
NFA看起来麻烦一点，但可以证明（定理3.1）必存在一个DFA和NFA等价。于是有一种题型叫NFA确定化，主要用状态转化矩阵重新建图。
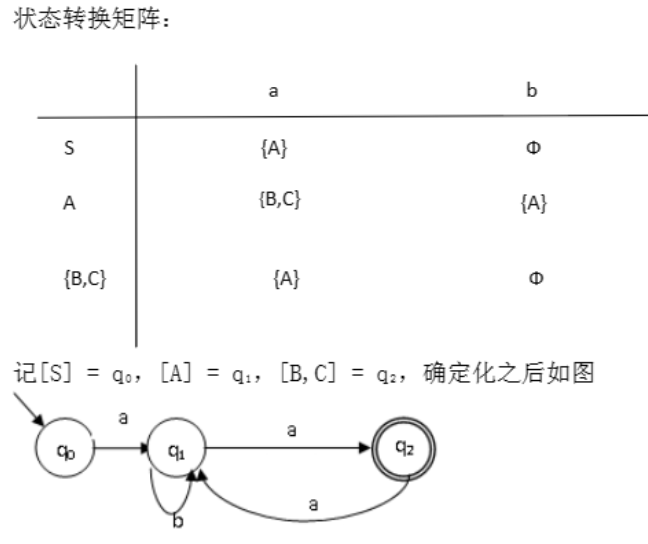
主要过程：设初始结点为S，以初始节点及近通过ε可达的结点（如果有ε表达式的话）为初始集合，以边的标记（就是边上写的那些小写字母）分类转移，每类转移所获得新的结点形成一个集合（如果有自环，则本身结点也算进下一个集合中），重复以上过程，直至没有新的集合产生为止。整个过程类似多源BFS，用转移矩阵（就是下面那种东西）记录，最后所获矩阵画成新的状态转换图，即为所求DFA。
例：将以下状态转换矩阵描述的NFA确定化。
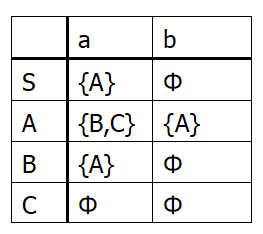
Ans：
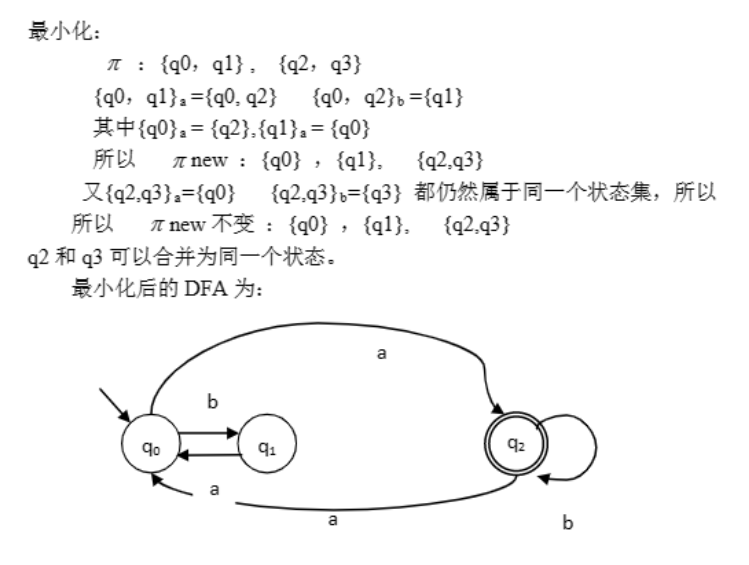
5. DFA最小化
DFA中可能会有多余状态，为化简DFA，有了DFA的最小化。这个过程一开始将状态分为终结和非终结，然后不断划分，最后合并同类状态。
主要过程：首先，将所有状态分为终结和非终结两个集合。对于每个集合，如果一组结点，能通过添加同一个字母，到达另一个集合，那么将它们从原来的集合中剥离出来，形成一个新的集合。重复以上过程，直至没有新集合产生为止。
例：将以下DFA最小化。
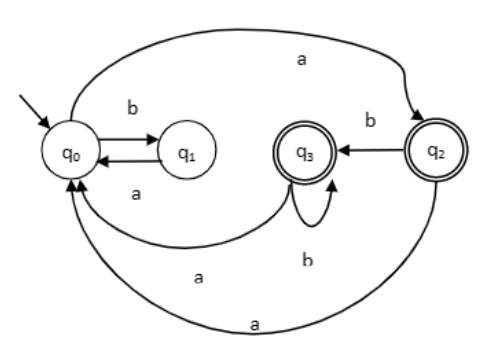
Ans:
