3 Pipelining
3.1 A Simple Implementation of DLX
Basic steps: IF→ID→EX→MEM→WB
Read Page 3-3 to 3-5 for details.
3.2 The Basic Pipeline for DLX
During MEM stage, branch instruction does nothing because it has store the res during IF stage.
Speedup for pipelining: ![]()
Example:
* Assume:
clock: 10ns;
ALU: 4 cycles, 40%;
branches: 4 cycles, 20%;
memory operations: 5 cycles, 40%.
* Suppose: due to skew and setup, pipelining machine adds to clock overhead=1ns.
* how much speedup we will gain from pipeline ?
Ans:
unpipelined: 10*(0.4*4+0.2*4+0.4*5)=44ns
pipelined: 10+1=11ns
speedup: 44/11=4
* clock cycle in pipeline must be equal, which means it should be the largest time for any stage.
3.3 The Major Hurdle of Pipelining–Pipeline Hazards
Structural hazards: resource conficts, and some functional unit is not fully pipelined, caused mainly by float calculations.
Data hazards: data used before calculated
Control hazards: related jump
3.4 Data Hazards
Solving data hazards with forwarding, and structural hazards will be sovled together.
RAW, the most common hazard
WAW, which will no happen in DLX
WAR, example in 3-27
But not all hazards can be solved with forwarding. (3-27)
About implementing Control for DLX Pipeline, to check the next 3 lines is enough to detect hazards. (3-33)
3.5 Control Hazards
When it comes to control hazards, the most nature idea is to stall two stages. To avoid stalls, we should both find out whether branch is taken and compute the taken PC.
We compute PC in EX at first. Now we move it into ID, which needs one more adder, and save 1 stall. In the same way, we write PC in IF.
Then we try to treat each branch as taken or not, and as a compromise, the branch delay slots appears. The best choice is to take irrelated lines. Second choice is to copy from the target, or untaken branch.
3.7 Overcoming Data Hazard with Dynamic Scheduling
**The Tomasulo Approach**
Refer 3-66 to recall the process.
Example:
Using the following code fragment:
Loop: LW R1, 0(R2); load R1 from address 0+R2
ADDI R1, R1, #1; R1=R1+1
SW 0(R2), R1; store R1 at address 0+R2
ADDI R2, R2, #4; R2=R2+4
SUB R4, R3, R2; R4=R3-R2
BNEZ R4, Loop; Branch to loop if R4!=0
Assume that the initial value of R3 is R2+396. Throughout this exercise use the classic RISC five-stage integer pipeline and assume all memory access take 1 clock cycle.
A. Show the timing of this instruction sequence for the RISC pipeline without any forwarding or bypassing hardware but assuming a register read and a write in the same clock cycle “forwards” through the register file. Assume that the branch is handled by flushing the pipeline. If all memory references take 1 cycle, how many cycles does this loop take to execute?
Ans: First, the cycle will repeat 396/4=99 times.
Without any optimizing, all the results can only be gained after MEM (the WB stage can write before read). The PC will be written at MEM. So the pipeline will be like the following:
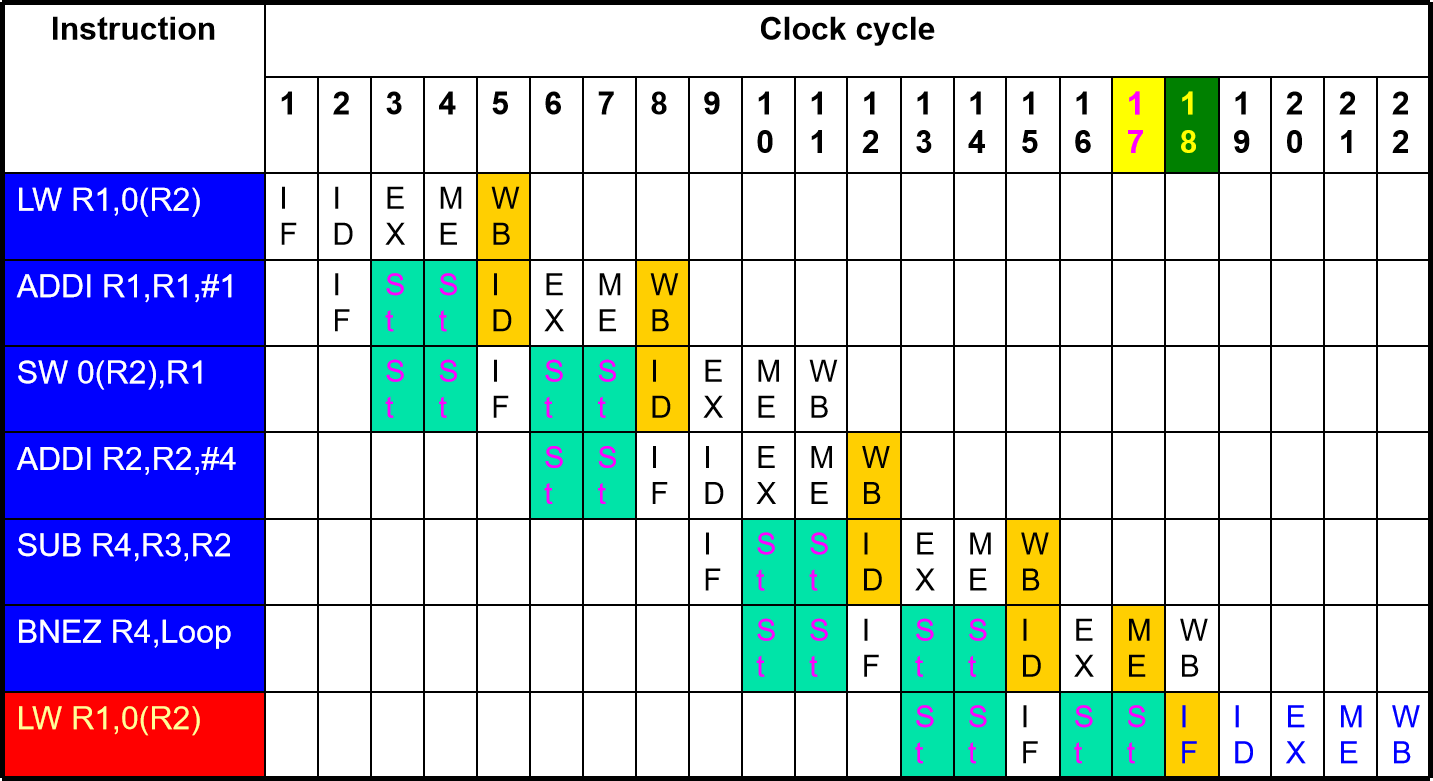
Thus, the answer will be 17×98+18=1684 clock cycles.
B. Show the timing of this instruction sequence for the RISC pipeline with normal forwarding and bypassing hardware. Assume that the branch is handled by predicting it as not taken. If all memory reference take 1 cycle, how many cycles does this loop take to execute?
Ans: Now the forwarding is allowed, so the only stall will occur in the situation where a register is used after load operation.

The answer is 10×98+11=991 clock cycles.
C. Assume the RISC pipeline with a single-cycle delayed branch and normal forwarding and bypassing hardware. Schedule the instructions in the loop including the branch delay slot. You may reorder instructions and modify the individual instruction operands, but do not undertake other loop transformations that change the number or opcode of the instructions in the loop. Show a pipeline timing diagram and compute the number of cycles needed to execute the entire loop.
Ans: The reordered program can be executed without any stalls:
Loop: LW R1,0(R2); load R1 from address 0+R2
ADDI R2,R2,#4; R2=R2+4
SUB R4,R3,R2; R4=R3-R2
ADDI R1,R1,#1; R1=R1+1
BNEZ R4,Loop; Branch to loop if R4!=0
SW -4(R2),R1; store R1 at address 0+R2
So the answer is 6×98+10=598 clock cycles.

 浙公网安备 33010602011771号
浙公网安备 33010602011771号