W. Tests for problem D
题意：给出一棵树，要求根据这棵树构造n条线段，线段两端取遍1-2n。对于树上所有连接(l, r)两结点的边，编号为l，r的两条线段相交且不包含；反之亦然。
解：限定条件后构造
如果两个结点之间没有直接相连，那么两条线段包含或相离。父节点与其全部儿子相交；兄弟节点之间包含或相离，但在上一条结论的前提下显然包含更好做。令一个结点的所有子节点一个套一个后与其父节点相交。对于一个节点的孙节点，应与该结点相离。于是可以这么构造：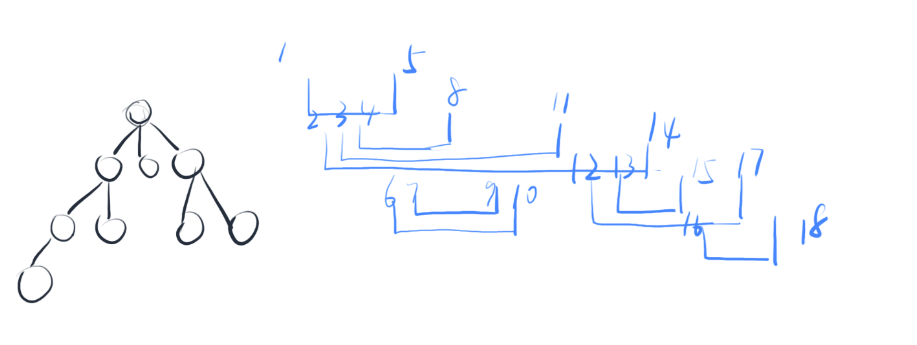
接下来给端点标号。每个结点代表一个线段，先标左端点，左右端点之间应该是孩子的数量，但看了看好像还要考虑兄弟孩子的个数，困扰。如果先遍历最右边的孩子的话事情就很简单了。记一个全局变量，按个加即可。好题！
X. Largest Unique Wins
题意：已知有n个人，m个数。每个人选择1-m中的一个数。令所有只被一个人选的数中最大的那个为a，那么选a的人得一分，其余人扣一份。如果没有这么一个数，所有人不得分。试为每个人选择1-m的概率赋值，使局面纳什均衡。
解：观察了一下样例，没弄懂小数怎么算的，不过以我的数学水平倒也正常。发现有很多0和1，观察一下，集中在前m列。假设n>=m，前m个人各拿一个数，思考后面的人是否可以乱选。思考结果是不可以，既然目前拿着这个数的只有我一个人，放弃这个数可能会使后面的人获得它从而胜利。那么每个数都有2个人选是否成立呢。成立。所以当n>=2m的时候，人们会两两一组拿一个数。考虑n<2m时的情况，应该也是2个人拿一个数，并且人们会从大的开始拿，这种情况下如果有人转而去拿小的数，那么大的数就会被零一人独占。考虑人数为奇数的情形。有一个人落单，并且这个人没有拿最大的数，而拿着大数字的人也不会阻止他目前只有一个人的情况，因为这样相当于把胜利给了同伴。这样看来输出0和1就可以。确实是这样。
