语法分析主要是将句子和语法树对应起来,明确其成分构成。接下来我们给一个句子添加一个末尾符号#,它为减少讨论作出卓越贡献。分析的时候将它也作为句子的一个符号分析。
1. 自顶向下
自顶向下的过程是在试图为一个句子找到它的语法树,也就是拿一个个推导语句试探,看是否能凑出这个句子。但直接递归回溯显然太过暴力,我们试图对文法进行一定限制,在此基础上寻找规律,以缩小查找范围,实现读一个或一些字符,就能知道该用哪条语句。
-2. 消除左递归
1. 文法的矩阵表达
文法:

矩阵表达,相乘后加变为或,非终结符号单独写在一个矩阵里,即为原文法:
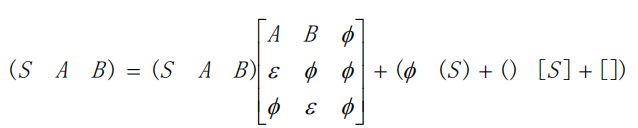
2. 进行一些神秘排列
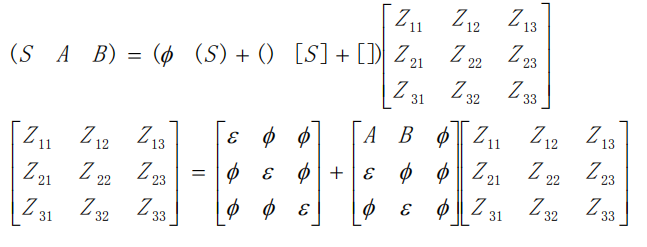
3. 对着写出来
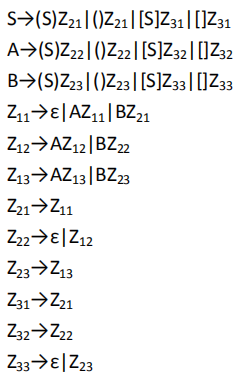
-1. 消除回溯
回溯是因为一个非终结符有多个候选式存在相同前缀,对它进行一些变换:

提取公共前缀,将剩余内容打包放进一个新的表达式。
1. 递归下降分析法
1. 简述
对每一非终结符号,编写一个子程序。如果读到的字符是某非终结符号的第一个终结符,那么调用其子程序。为了描述前面最长的那句话,引入FIRST集和FOLLOW集。
FIRST集为一个非终结符推导出来的第一个终结符;FOLLOW集为一个非终结符后第一个被推导出来的终结符。
例:
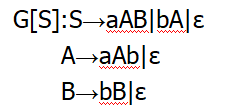

如果A->B,那么B的FIRST集也是A的FIRST集的子集;FOLLOW集同理。对于A->CD,c的FOLLOW集会是D的FIRST集。
2. 流程
每次读一个字符->确定接下来调用哪个非终结符的子程序->根据其FOLLOW集判断接下来调用哪个子程序
2. LL(1)分析法
1. LL(1)文法
从左到右,使用最左规约,每次读一个字符即可确定如何推导。
LL(1)文法的判断:
对于类似于A->α|β,FIRST(α)∩FIRST(β)=Φ;若α可推出空产生式,则FIRST(α)∩FOLLOW(A)=Φ.
2. 简述
LL(1)分析法是一种预测分析法。它使用一个栈,栈底为#。如果栈顶和下一个字符可以形成推导,即在一张分析表里找到表达式(预测在此情况下用这个表达式),就将表达式的右部逆序压进栈(来分析最左边的符号)。如果下一个字符和栈顶匹配,则开始读下下个字符。可以看到,这个方法的关键在于如何构建分析表。
分析表求法:
文法
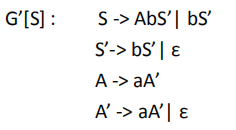
求每条产生式求FIRST集和FOLLOW集

对应填进表里,一般先用FIRST集,如果为空,用FOLLOW集
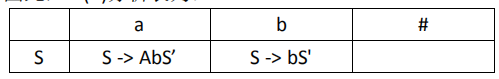

2. 自底向上
如果说自顶向下分析的重点在于选择哪条语句,那么自底向上分析就在于规约哪些终结符。
对于第一第二个方法,首先定义什么是优先。在自底向上中,可能会出现一些挨在一起的字符恰好能用表达式规约,但实际上它们在语法树的不同深度。为了解决这一问题,我们从语法出发,定义应当先被规约的字符,也就是叶子节点,优先于后被规约的字符。
注意这里的优先是有严格顺序的,如果a先于b被规约,那么说a>b,但这不意味着b<a。放在语法树上更加清晰:
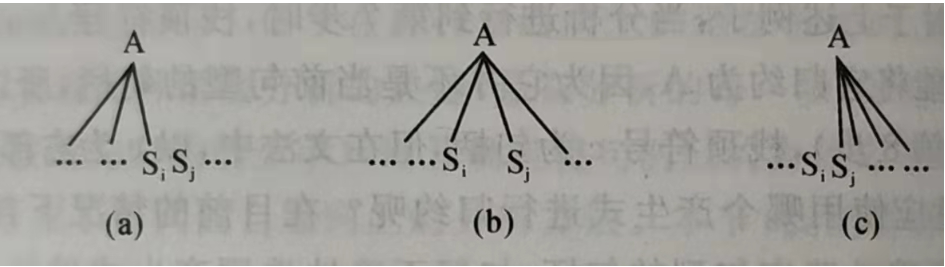
对于(a),Si>Sj;对于(b),Si=Sj;对于(c),Si<Sj;这些比较是针对某个特定语法树的相邻两个符号而言,不相邻没什么研究意义,而换一个语法树可能大小关系就发生变换。当然,我们不喜欢这种语法。
接下来考虑分析的过程。现在我们知道了两个相邻符号的大小关系。假设句子的某一段相邻关系长成这样:...<<==>>>...,那么中间那一段就应该被规约了。依旧引入一个栈,栈底为#,存放正在分析的符号。如果下一个符号小于等于栈顶,入栈;如果大于栈顶,找到前一个小于号,将中间部分规约。
可以想象程序里会出现一坨map
对于不同的分析表,引入简单优先分析和算符优先分析。
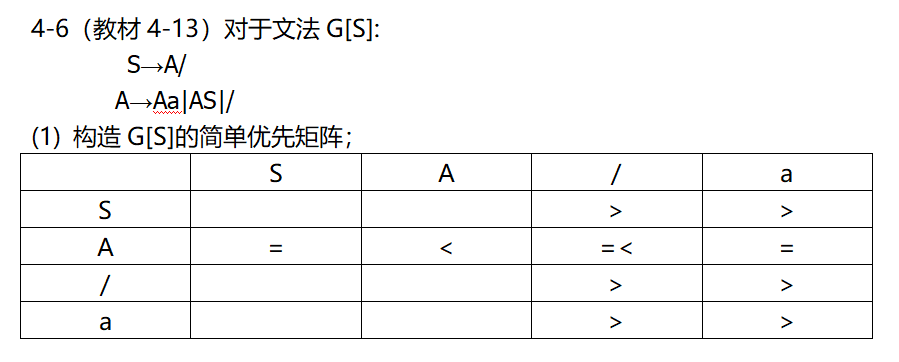
1. 简单优先分析
也就是上面描述的那个规约过程,从中可以看出,应该对于所有的终结符和非终结符构建分析表。
不太好构建,硬编出点句子看吧。
2. 算符优先分析
简单优先分析分类太过细致,事实上有些比较是不必要的。例如(A+B)中,我们知道+的优先级最高,括号的优先级相等,至于具体的A和B是什么实际上不重要。这种想法引出了算符优先分析,即只关心终结符之间的优先级。为了能够使用这种简洁的分析,又对文法进行了一些规定:表达式右部最多只能有一个非终结符,不然我们就不得不考虑非终结符之间的优先级了。


尾:优先函数
如果用二维数组来存储分析表可能会花费太多空间,我们希望存在一个函数,将符号映射后保持其大小关系,也就是优先函数。优先函数有两种构造方法,一是Bell方法,二是Floyd方法。(拼起来就能求最短路了是吧)
Bell方法:对每个符号进行拆点操作,拆成f和g,分别对应其在符号左边和右边的情况。接下来对于分析表里的内容,以朝大于号开口的点为起点,另一个为终点连一条边。最终值为该点闭包大小。
Floyd方法:初始时为每个值都设为1,然后多次遍历分析表。碰到大小关系就令大的比小的大1,直到值不变为止。
以上方法都对文法本身有很多限制,1965年,D.Knuth提出了LR(k)分析技术,意为从左到右,使用最右推导,每次看k个输入符号就能判断下一步动作,事实上LR和之前LL的意思是一样的(
其对语法作了更细致的分析,构建了分析动作表和状态转移表。分析动作表将语法分析的过程分为不同状态,设计了每个状态碰到一个终结符应该做什么;状态转移表是说当发生规约或新加一个非终结符号时转移到的下一状态。当状态转移到accepted的时候,说明分析成功。意会一下就是分析动作表针对终结符,状态转移表针对非终结符。
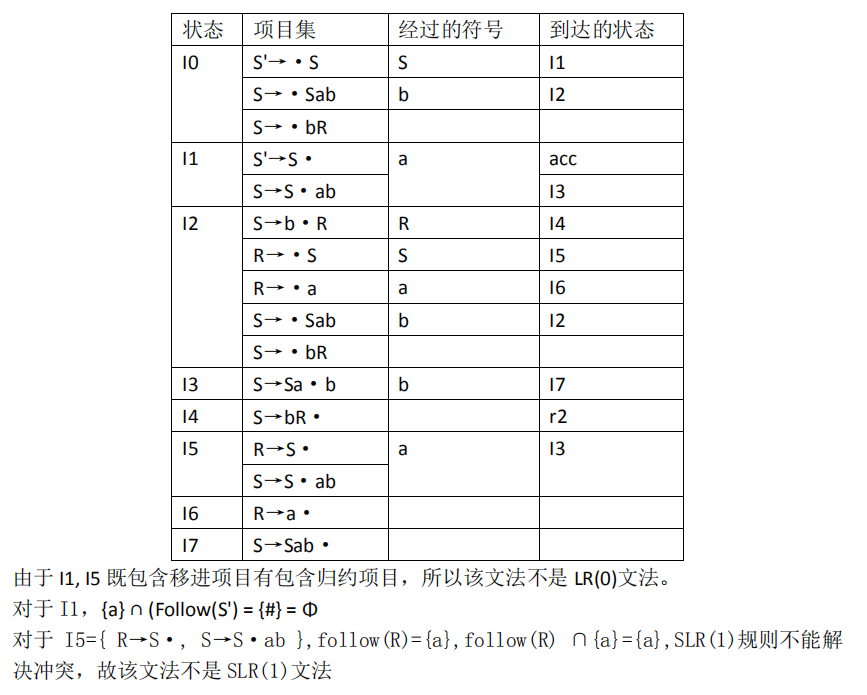
介于我们都是一个符号一个符号读入,所以把所有推导式细分为读到哪一个字符的状态,在读完的字符后加一个点。每一个状态叫项目(item),另外给推导式里加上S'->S,构成所谓的项目集规范族:

接下来将这个规范族里的项目分成几类,也就是我们所说的状态。这个过程和NFA确定化很像,都是从一些结点出发,求其闭包,即能推出哪些东西。再根据现有状态,读入下一个字符,形成接下来若干个状态。
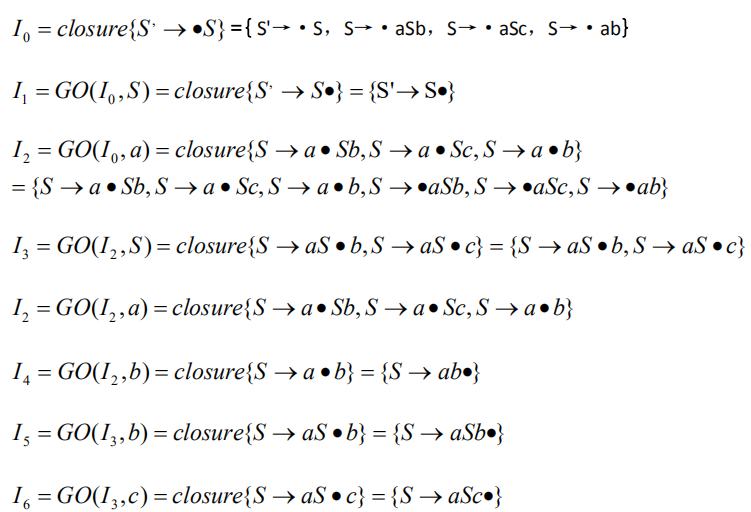
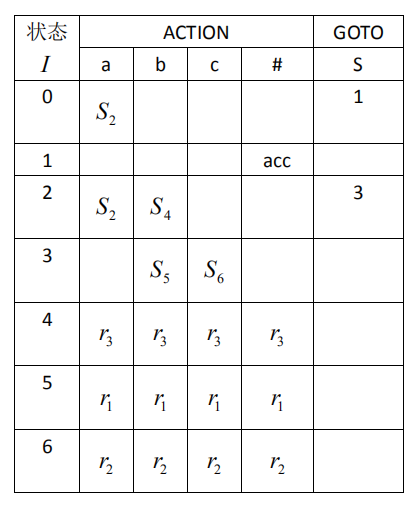
然后把推的过程写成表格,就是分析表了。终结状态用r表示,下标就是那个表达式在题目里的顺序。。。
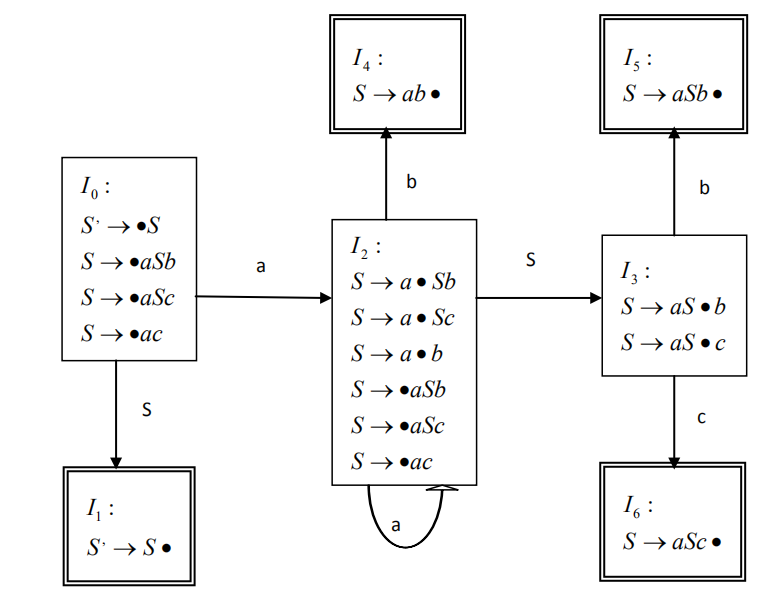
或者有的题会要求画DFA。
3. LR(0)分析法
先推荐一个蛮好玩的网站:LR(0) Parser Visualization
当上面那个表能填出来的时候,它就是LR(0)文法了。
4. SLR(1)分析法
SLR的S是simple,意为那个表冲突时,可以根据FOLLOW集和往后看一个字符来唯一确定用哪个表达式。在判断是否为SLR(1)文法时,需要判断有公共前缀的几个表达式FOLLOW集是否有交集。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号