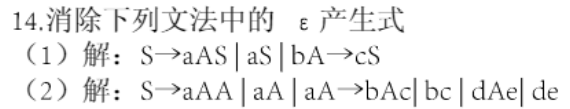教材:《编译原理》 西北工业大学出版社 主编:蒋立源 康慕宁
这本书不太说人话,因为概念严谨描述出来看着就很晕,下文主要在意会它到底是个什么东西以及干了什么事。
第二章 前后文无关文法和语言
1. 概念介绍
文法:类似于下面的递推式
G[S]:S→AB A→aA|ε B→bBc|bc
其中,能继续往下推的为非终结符号,通常用大写字母表示,记作VN (nonterminate);反之为终结符号,用小写字母表示,记作VT (terminate)。这些递推式叫产生式,记作P;最开始用来推导的叫开始符号,记作S,通常也直接写作S。ε为空符号串。
综上,一个文法可以表示为G[S]=(VN ,VT ,P ,S).
句子:文法能推出的一个全是终结符号的符号串。
语言:所有句子的集合。
接下来对句子进行分析,也就是句型分析。我们主要关心一个句子是怎么被推导出来的,以及它的逆过程,规约。
不妨假设产生式的左部只有一个非终结符。
为了统一,定义规范推导和规范规约。
规范推导:也叫最右推导,意为每次拿最右边的非终结符号继续推;
规范规约:也叫最左规约,每次拿最左边能规约的一串东西规约。
推导的过程很容易用 树 这一结构表示,编译原理中称之为语法树。每次推导我们给一个非终结符号添加几个子节点,规约的时候把子树缩为其父节点。如果一个句子有两个本质不同的语法树,那么这句话具有二义性。
为了方便描述规约这一过程,我们又造出了几个概念:
短语:若干相邻叶子结点组成的东西。容易看出短语是相对于非终结符而言的,也就是一个非终结符生成的终结符串。
直接短语:只推导了一步得到的短语。
句柄:下一步规约要规约掉的东西。肯定是一个直接短语。如果有多个直接短语,选择最左边的那个。放到语法树上,就是最左简单子树的叶子节点。
对于一个文法,出于人类的本能,我们希望它足够简洁。适当的ε,也就是空产生式,便于我们描述一种语言(比如第三章把一个正则式转化为文法时)。但如果最后时不时生成一个空串就没有必要了。为了化简这种情况,出现了几个算法。ε-产生式的消除
还有一种产生式是单产生式,也就是最后只有一个字符的情况。不过这个化简好像不考就先不写了(……
上述描述都是建立在产生式的左部只有一个非终结符的基础上。其他情况各自有自己的名字,也就是文法的Chomsky分类。
0型文法:无限制文法。长成什么样都可以
1型文法:类似于αAβ->...,也叫上下文相关文法,只有在特定上下文中才能替换。并且定义它的长度永远不会缩短。
2型文法:就是上面举例子的文法
3型文法:产生式右部只有一个非终结符号,也叫正规文法。
现在你已经简单了解了文法,来试试这些题吧
2. 习题存档
1. 文法和语言的互相转换
L={anbn|n≥0}
ans:S->aSb|ε
L={anbmcp|n,m,p≥0}
ans:S->aS|X, X->bX|Y, Y->cY|ε

可能是我上课没听,但好像没有什么正规方法,手玩几个意会一下(
2. 最左最右推导
硬推
3. 证明二义性文法
找出两个语法树
4. 消除空产生式
往算法里套