Educational Codeforces Round 136 C. Card Game

题意：有1-n的一个排列，其中n是偶数，A和B两个人拿这副牌玩游戏，两个人绝顶聪明。A拿一半牌，B拿一半牌。规则很简单，A先手出牌，如果B有比他大的牌，那出一张比他大的牌，这一轮结束，下一轮B先手出牌，规则同上。当某一方没有比对方大的牌时输掉。如果两个人牌都出完了也没有分出胜负，那么算平局。求所有发牌可能中A赢的次数，B赢的次数和平局次数，答案模998244353.

解：观察一下样例发现平局始终是1，想想很合理，那么先假设平局的确是1（。显然当A拿到最大的牌时他已经赢了，那么考虑B拿到最大牌的情景。

• B拿到了最大的牌，那么A就要想办法把他最大的牌钓出来，不然下一局B先手，A就寄了。
• 显然拿n-1钓最合适。如果A没有n-1，那么就是B有n-1，不管A出什么，B都可以出n-1，然后再出n，赢下这把。
• 如果A有n-1，那么n和n-1都出掉，A并没有损失。
• 当然也可以说：假设A有n-2，那A拿n-2钓n，留着n-1，但下一局留着n-2和留着n-1有什么区别呢，所以还是把n-1出掉吧。
• 故可以画出这张图，其中A_n表示A有n这张牌：

　　　

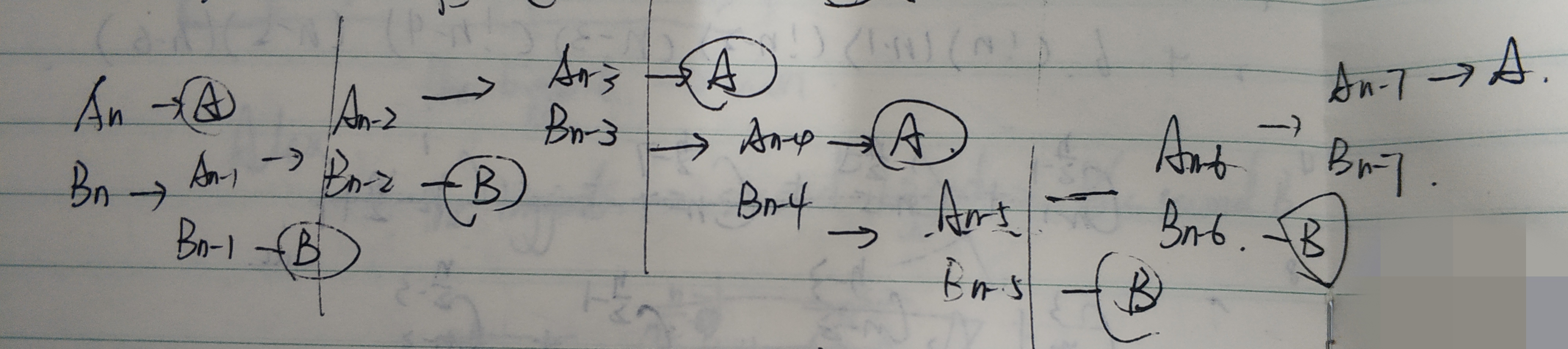
• 推一下组合数公式，可得：

　　　

• 以及由图得，平局的确只有一种可能。

代码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define maxx 200005
#define inf 1000000009;
#define mod 998244353
ll c[65][65]={0};
void init(){
    for(int i=0;i<62;i++){
        for(int j=0;j<=i;j++){
            if(!j)
                c[i][j]=1;
            else{
                c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
            }
        }
    }
}
signed main(){
    init();
    int T;
    cin>>T;
    while(T--){
        int n;
        scanf("%d",&n);
        ll ans=0;
        int up=3,down=4;
        while(n>down){
            ans=(ans+c[n-down][n/2-up])%mod;
            if(n>down+1)
                ans=(ans+c[n-down-1][n/2-up])%mod;
            down+=4,up+=2;
        }
        ans=(ans+c[n-1][n/2-1])%mod;
        printf("%lld %lld 1\n",ans, (c[n][n/2]+mod-ans-1)%mod);
    }
    return 0;
}