第四章 插值与拟合
给定一系列的点,求多项式函数
可以用n个点确定n个未知量,但此方程组病态,误差极大。
1.插值余项(PPT1
用于估算误差(P76
2.拉格朗日插值多项式
为每个点构造一个格式统一的函数,使得取到该点时值为1,其余点均为0.
一种构造:
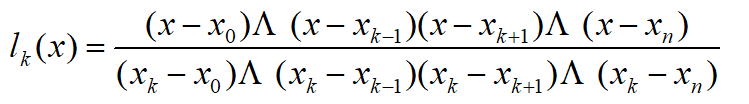
取2点,为线性插值,代码:

function y=xianxing(X,Y,x) x0=X(1); y0=Y(1); x1=X(2); y1=Y(2); l0=(x-x1)/(x0-x1); l1=(x-x0)/(x1-x0); y=y0*l0+y1*l1;
取3点,为抛物插值,代码:

function y=paowu(X,Y,x) x0=X(1); x1=X(2); x2=X(3); y0=Y(1); y1=Y(2); y2=Y(3); L0=(x-x1)*(x-x2)/(x0-x1)/(x0-x2); L1=(x-x0)*(x-x2)/(x1-x0)/(x1-x2); L2=(x-x0)*(x-x1)/(x2-x0)/(x2-x1); y=y0*L0+y1*L1+y2*L2;
误差分析:套余项式,注意代最近的点。(P79
3.分段低次插值
提高插值多项式的次数会产生龙格现象,因此换用多个低次拼凑。
分段线性插值
代码:

function yy=fdxx(x,y,xx) n=size(x,2); for i=1:n-1 if x(i)<xx&&xx<x(i+1) L1=(xx-x(i+1))/(x(i)-x(i+1)); L2=(xx-x(i))/(x(i+1)-x(i)); yy=L1*y(i)+L2*y(i+1); break; elseif x(i)==xx yy=y(i); end end end
分段抛物插值
代码:

function y=fdpw(xi,yi,x) n=size(xi,2); if x<xi(2) L1=(x-xi(1))*(x-xi(3))/(xi(1)-xi(2))/(xi(1)-xi(3)); L2=(x-xi(1))*(x-xi(3))/(xi(2)-xi(1))/(xi(2)-xi(3)); L3=(x-xi(1))*(x-xi(2))/(xi(3)-xi(1))/(xi(3)-xi(2)); y=L1*yi(1)+L2*yi(2)+L3*yi(3); elseif x>xi(end-1) L1=(x-xi(end-1))*(x-xi(end))/(xi(end-2)-xi(end-1))/(xi(end-2)-xi(end)); L2=(x-xi(end-2))*(x-xi(end))/(xi(end-1)-xi(end-2))/(xi(end-1)-xi(end)); L3=(x-xi(end-2))*(x-xi(end-1))/(xi(end)-xi(end-2))/(xi(end)-xi(end-1)); y=L1*yi(1)+L2*yi(2)+L3*yi(3); else for k=2:n-1 if xi(k+1)>x if abs(x-xi(k))<abs(x-xi(k+1)) i=k-1; else i=k; end L1=(x-xi(i+1))*(x-xi(i+2))/(xi(i)-xi(i+1))/(xi(i)-xi(i+2)); L2=(x-xi(i))*(x-xi(i+2))/(xi(i+1)-xi(i))/(xi(i+1)-xi(i+2)); L3=(x-xi(i))*(x-xi(i+1))/(xi(i+2)-xi(i))/(xi(i+2)-xi(i+1)); y=L1*yi(i)+L2*yi(i+1)+L3*yi(i+2); end end end end
三次样条插值
分段线性和分段抛物插值会导致曲线不平滑。三次样条插值用多个三次函数拼接,保证曲线二阶导连续。一个三次函数有4个未知数,n个三次函数就有4n个未知数,当前点函数值、当前点连续、一阶导连续、二阶导连续有4n-2个已知量,还差两个,因此需要2个初值,一般为两端点的一阶导或二阶导。实际应用中用二阶导表示函数,这样只需计算n+1个未知数,从而推导出简便的式子(4.52)。(P91-94
代码:

function s=threesimple1(X,Y,x,y0,yn) % 三次样条插值函数第一类型代码 % s函数表示三次样条插值函数插值点对应的函数值 % 根据三次样条参数函数求出的D,h,A,g,M % x表示求解插值点函数点,X为已知插值点 [D,h,A,g,M]=Mspline3(X,Y,y0,yn) n=length(X); m=length(x); for t=1:m for i=1:n-1 if (x(t)<=X(i+1))&&(x(t)>=X(i)) p1=M(i,1)*(X(i+1)-x(t))^3/(6*h(i)); p2=M(i+1,1)*(x(t)-X(i))^3/(6*h(i)); p3=(A(i,1)-M(i,1)/6*(h(i))^2)*(X(i+1)-x(t))/h(i); p4=(A(i+1,1)-M(i+1,1)/6*(h(i))^2)*(x(t)-X(i))/h(i); s(t)=p1+p2+p3+p4; break; else s(t)=0; end end end end function [D,h,A,g,M]=Mspline3(X,Y,y0,yn) % 自然边界条件的三次样条函数(第一种边界条件) % 此函数为M值求值函数 % D,h,A,g,M输出量分别为系数矩阵D,插值宽度h,差商表A,g值,M值 n=length(X); A=zeros(n,n);A(:,1)=Y';D=zeros(n,n);g=zeros(n,1); for j=2:n for i=j:n A(i,j)=(A(i,j-1)- A(i-1,j-1))/(X(i)-X(i-j+1)); end end for i=1:n-1 h(i)=X(i+1)-X(i); end for i=1:n D(i,i)=2; D(1,2)=1; D(n,n-1)=1; if (i==1) g(i,1)=6/h(i)*(A(2,2)-y0); elseif (i==n) g(i,1)=6/h(i-1)*(yn-A(i,2)); else g(i,1)=(6/(h(i-1)+h(i)))*(A(i+1,2)-A(i,2)); end end for i=1:n-2 u(i)=h(i)/(h(i)+h(i+1)); n(i)=1-u(i); D(i+1,i+2)=n(i); D(i+1,i)=u(i); %改到这里 end M=D\g; %M=[0;M;0]; end
4.曲线拟合的最小二乘法(PPT2
由于采样点有误差,因此希望得到一个更接近真实规律的近似表达式,使得偏差平方和最小。求法为先根据观察选择一个函数,再求误差表达式取得极小值的条件,即一阶导等于0推出的方程组(P104
方程组是线性的比较好解,因此我们通过换元把函数化为线性形式,例如指数形式表达式取对数等。
代码:

function p=leastsquare(x,y,m) A=zeros(m+1,m+1); b=zeros(1,m+1); for i=0:m for j=0:m A(i+1,j+1)=sum(x.^(i+j)); end b(i+1)=sum(x.^i.*y); end p=vpgauss(A,b);
第五章 数值微分与数值积分
1.数值微分(PPT1
根据离散点函数值推断某点导数近似值。
求法:通过构造插值多项式得到数值微分公式及其余项,常用其二级结论两点公式、三点公式计算导数(P117
2.数值积分(PPT2
根据离散点函数值推断区域上函数积分值。
求法:同样通过构造插值多项式代替被积函数,得到插值型求积公式及其余项(P121-122
数值积分公式的代数精度
以代数多项式为准,对任意不高于m次代数多项式准确成立,而m+1次不成立,称该数值积分公式代数精度为m。例:P123
牛顿-科茨方法
用n次插值函数多项式近似被积函数。
复合就是将积分区域分成n段,每段按对应方法积分。误差是步长的n次方,称为n阶方法。
(复合)梯形公式
用梯形代替步长内积分值。代数精度1,二阶方法。代码:

function x=tixing(a,b,n) f=@(x) x/(4+x*x); x=0; h=(b-a)/n; for k=1:n-1 x=x+f(a+k*h); end x=h*(f(a)+x*2+f(b))/2; end
(复合)辛普森方法
用二次插值函数多项式近似。代数精度3,四阶方法。代码:

function t=simpson(a,b,n) x=0; h=(b-a)/n; f=@(x) x/(4+x*x); for k=0:n-1 x=x+f(a+k*h+h/2); end y=0; for k=1:n-1 y=y+f(a+k*h); end t=h*(f(a)+4*x+2*y+f(b))/6;
(复合)科茨公式
用四次插值函数多项式近似。代数精度5,六阶方法。
龙贝格算法
近似值精度与步长选择有关,计算过程中可以通过判断当前误差调整步长以提高精度,但其计算缓慢。龙贝格算法以不同的权重组合不同区间长度的求积公式(几何意义上可以理解为在区间合适的位置划线,例如在中间画直线替代在顶上,使多出来的和少掉的抵消),从而抵消主要误差。视其误差正负号来判断组合的时候的符号。
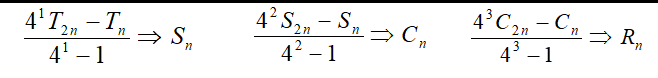
代码:

function x=Romberg(a,b,eps) %龙贝格算法求积分 %a,b分别为上下限,eps为精度 f=@(x) sqrt(400*sin(x)*sin(x)+100*cos(x)*cos(x)); k0=4; k1=10; T=zeros(4,1); t=zeros(4,1); T(1)=(b-a)*(f(a)+f(b))/2; k=1; while k<=k1 t(1)=T(1)/2; temp=0; for i=1:2^(k-1) temp=temp+f(a+(2*i-1)*(b-a)/2^k); end temp=temp*(b-a)/2^k; t(1)=t(1)+temp; for i=2:min(4,k+1) t(i)=((4^i)*t(i-1)-T(i-1))/(4^i-1); end if k>=k0 if abs(t(4)-T(4))<eps x=t(4); break; end end T=t; k=k+1; end
第六章 常微分方程的数值解法
由于高阶常微分方程可以化为一阶常微分方程,故本章只解一节常微分方程初值问题的数值解法。答案并不需要得到精确的函数表达式,只要能获得想要点的估计值即可。
如果截断误差为步长的p+1次方,那么此方法为p阶方法。
1.欧拉方法
将函数区间n等分,得到n+1个等分点上的函数值。已知每个函数值是待求函数的导数,用直线代替该区间上的待求函数则是该线段的斜率,画出一段,再连下一段,得到一堆折线,因此又称欧拉折线法。欧拉方法是一阶方法。

代码:

function Euler(a,b,n,y0) f1=@(x,y) 2*x/3/y/y; f2=@(x) (1+x*x)^(1/3); h=(b-a)/n; x=a:h:b; y=zeros(1,n); y(1)=y0; for i=1:n y(i+1)=y(i)+h*f1(x(i),y(i)); end x2=a:h:b; y2=zeros(1,n); for i=1:n+1 y2(i)=f2(x2(i)); end plot(x,y,'-o'); hold on; plot(x2,y2,'-ro'); for i=1:n+1 y2(i)=abs(y(i)-y2(i)); end display(y2);
2.改进欧拉方法
欧拉方法向前作折线,也就是向前差分。改进欧拉方法向后差分,得到一个隐函数,计算量变大,稳定性增强,但仍是一阶方法。隐式欧拉公式和欧拉公式的误差主要部分符号相反,因此将它们两个加起来除以2,得到梯形公式,是二阶方法。再用显式欧拉公式算个初值,联合使用,得到改进欧拉方法,其仍为二阶方法(P151
代码:

function Euler2(a,b,n,y0) f1=@(x,y) 2*x/3/y/y; f2=@(x) (1+x*x)^(1/3); h=(b-a)/n; x=a:h:b; y=zeros(1,n); y(1)=y0; for i=1:n y(i+1)=y(i)+h/2*(f1(x(i),y(i))+f1(x(i+1),y(i)+h*(f1(x(i),y(i))))); end x2=a:h:b; y2=zeros(1,n); for i=1:n+1 y2(i)=f2(x2(i)); end plot(x,y,'-o'); hold on; plot(x2,y2,'-ro'); for i=1:n+1 y2(i)=abs(y(i)-y2(i)); end display(y2);
3.龙格-库塔法
欧拉方法与改进欧拉方法的延伸,由微分中值定理引出。欧拉方法中以区间左端点斜率作为区间折线斜率,欧拉改进方法以左右端点平均值作为其斜率,龙格-库塔法想要用各种各样的方法近似这个斜率的真值,也就是找微分中值定理里那个代表不知道是啥的 ζ ,比如多取几个点,求平均值。但这还不够,最终还需要找几个参数,求得加权平均值。
代码(经典四阶方法,也被称为R-K法):

function RungeKutta(a,b,n,y0) h=(b-a)/n; f1=@(x,y) 2*x/3/y/y; f2=@(x) (1+x*x)^(1/3); h=(b-a)/n; x=a:h:b; y=zeros(1,n); y(1)=y0; for i=1:n xx=x(i); yy=y(i); k1=f1(xx,yy); k2=f1(xx+h/2,yy+h/2*k1); k3=f1(xx+h/2,yy+h/2*k2); k4=f1(xx+h,yy+h*k3); y(i+1)=y(i)+h/6*(k1+2*k2+2*k3+k4); end x2=a:h:b; y2=zeros(1,n); for i=1:n+1 y2(i)=f2(x2(i)); end plot(x,y,'-o'); hold on; plot(x2,y2,'-ro'); for i=1:n+1 y2(i)=abs(y(i)-y2(i)); end display(y2);

