计算方法1-3章存档

线上考试查询用

教材：数值计算方法  第3版  朱建新  李有法  编  高等教育出版社

第一章  误差

绝对误差：e*(x)

相对误差：e_r(x)=e*(x)/x

舍入误差：计算机计算时产生的误差

误差传播规律：（二元为例）P8

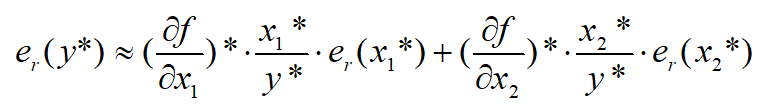
 迭代算法稳定性：P9

第二章  非线性方程求根

1.二分法

代码：

function [it,l]=half(l,r,eps)
f=@(x) exp(x)+10*x-2;%方程
it=0;%迭代次数
it_limit=30;%迭代次数限制
while r-l>=eps
    a=feval(f,l);
    b=feval(f,r);
    if a*b>0
        fprintf('不符合要求\n');
        break;
    else
        it=it+1;
        if it>it_limit
            fprintf('迭代次数过大\n');
            break;
        end
        mid=(l+r)/2;
        x=feval(f,mid);
        if a*x<0
            r=mid;
        else
            l=mid;
        end
    end
end
    

　　　　误差分析：(b-a)/2^k+1

　　2.迭代法

　　　　普通迭代：将方程变形为x=g(x)，任选一点x₀，获得x₁=g(x₀)，x₁向y=x作交点，将纵坐标转为横坐标，重复以上过程。

　　　　几何意义：

　　　　

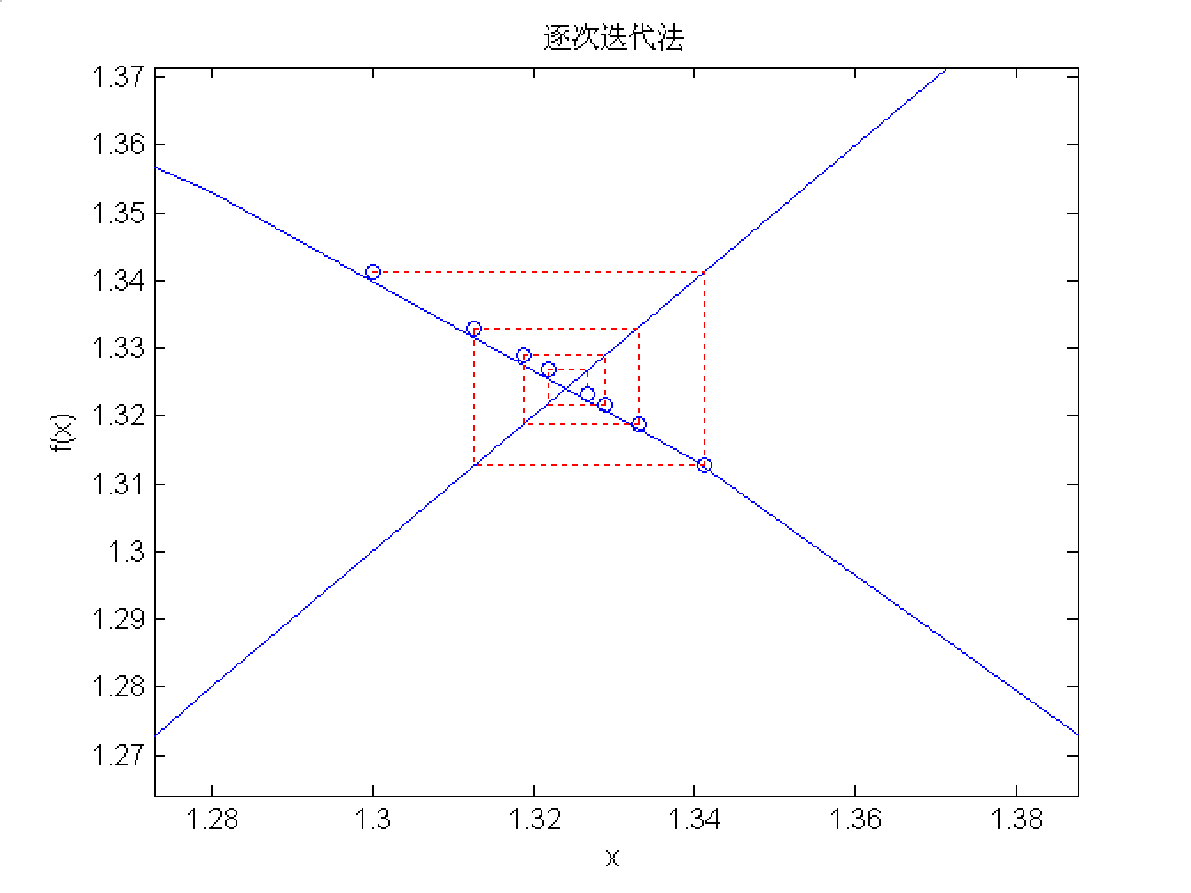
　　　　迭代法收敛的2个充分条件：P18

　　　　牛顿迭代法

任选一近似根，方程在近似根处展开，以一阶导逼近真值。

几何意义：在近似根处作切线，以切线和x轴交点横坐标作为新近似根，重复以上过程。

代码：

function[it,x]=newton(x0,eps)
f=@(x) exp(x)+10*x-2;%原函数
fd=@(x) exp(x)+10;%导数
it_limit=30;%迭代次数限制
it=0;%迭代次数
x=x0;
xb=x+999;
while abs(x-xb)>=eps
    if it>it_limit
        fprintf('迭代次数超限：it=%3.0f\n',it);
        break;
    end
    y=feval(f,x);
    y1=feval(fd,x);
    if abs(y1)<1e-10
        fprintf('导数为零')
        break;
    end
    xb=x;
    x=xb-y/y1;
    it=it+1;
end

充分条件：P23

误差：|x_k+1-x_k|

收敛阶

 

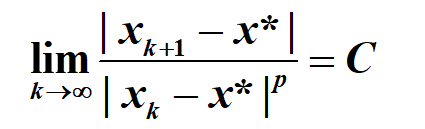
　　　　牛顿法收敛阶分析：P29（转化为余项）

 第三章  线性代数方程组的解法

1.高斯消元法（PPT1

顺序消元

代码：（作业要求，用的时候把round去了

function x=gauss(A,b)
N=size(A);
n=N(1);
x=zeros(n,1);
for i=1:(n-1)
    for j=(i+1):n
        if(A(i,i)==0)
            disp('0 error');
        end
        m=roundn(A(j,i)/A(i,i),-4);
        A(j,i:n)=roundn(A(j,i:n)-m*A(i,i:n),-4);
        b(j)=roundn(b(j)-m*b(i),-4);
    end
end
x(n)=roundn(b(n)/A(n,n),-4);
for i=n-1:-1:1
    x(i)=roundn((b(i)-sum(A(i,i+1:n)*x(i+1:n)))/A(i,i),-4);
end

2.列主元消元法

每次排序选最大的主元，避免舍入误差

代码：

function x=vpgauss(A,b)
N=size(A);
n=N(1);
x=zeros(n,1);
zz=zeros(1,n);
for i=1:(n-1)
    [~,p]=max(abs(A(i:n,i)));%~表示忽略第一维
    zz=A(i,:);%获取第i行
    A(i,:)=A(p+i-1,:);
    A(p+i-1,:)=zz;
    temp=b(i);
    b(i)=b(i+p-1);
    b(i+p-1)=temp;%交换
    for j=(i+1):n
        if(A(i,i)==0)
            disp('0 error');
        end
        m=A(j,i)/A(i,i);
        A(j,i:n)=A(j,i:n)-m*A(i,i:n);
        b(j)=b(j)-m*b(i);
    end
end
x(n)=b(n)/A(n,n);
for i=n-1:-1:1
    x(i)=(b(i)-sum(A(i,i+1:n)*x(i+1:n)))/A(i,i);
end

3.三角分解法 -> 追赶法

P48、49

4.范数（PPT2

模（距离）的延伸定义

性质：1.非负性  2.齐次性  3.三角不等式  P52

矩阵三种范数：P54

5.迭代法（PPT3

已知AX=b，寻找一个迭代矩阵B，令X=BX+f，重复计算，逼近答案。可视作非线性方程求根在高位线性情况的延伸。

雅可比迭代法

把每条方程解出一个变量表达式，提出系数矩阵作为B和f。

分量表达式：P57

代码：（参数里的b和x竖着

function [n,it,y] = Jacobiit(A,b,x,it_limit)
fprintf('雅可比迭代法\n'); 
D=diag(diag(A));
B=inv(D)*(D-A);
n=norm(B);
b=inv(D)*b;
it=0;
while 1
    it=it+1;
    if(it>it_limit)
        fprintf('迭代次数超界 \n');
        break
    end
    y=B*x+b;
    if(norm(y-x,inf)<1e-3)%求范数
        break;
    else
        x=y;
    end
end

高斯-赛德尔迭代法

把雅可比迭代法前面解出的变量马上代入后面，希望能求得更快。但有时雅可比快，有时高斯-赛德尔快。

分量表达式：P58

代码：

function [it,y] = GaussSeidelit(A,b,x,it_limit)
fprintf('高斯-赛德尔迭代法\n'); 
DL=tril(A);
B=inv(DL)*(DL-A);
b=inv(DL)*b;
it=0;
while 1
    it=it+1;
    if(it>it_limit)
        fprintf('迭代次数超界 \n');
        break
    end
    y=B*x+b;
    if(norm(y-x)<1e-3)
        break;
    else
        x=y;
    end
end

收敛条件与误差估计

P59

雅可比和高斯-赛德尔迭代收敛充分条件：1.按行或按列严格对角占优  2.A正定  

矩阵迭代收敛充要条件：迭代矩阵B谱半径绝对值小于1

逐次超松弛迭代法

给高斯-赛德尔迭代法选一个玄学松弛因子w（P65

代码：

function [it,y] = SORit(w,A,b,x,it_limit)
fprintf('逐次超松弛迭代法\n');
D=diag(diag(A));
L=-tril(A,-1);%提取下三角
U=-triu(A,1);%提取上三角
B=inv(D-w*L)*((1-w)*D+w*U);
b=w*inv(D-w*L)*b;
it=0;
while 1
    it=it+1;
    if(it>it_limit)
        fprintf('迭代次数超界 \n');
        break
    end
    y=B*x+b;
    if(norm(y-x)<1e-3)
        break;
    else
        x=y;
    end
end