新学的差分约数系统，大概用来解决长成这样的问题：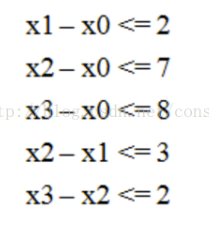
如果不等号是小于，就换成小于等于。大于同理。
令所有x为结点，常数为边权连图：
符号为小于等于时，两点间最短路为两点差的最大值。
符号为大于等于时，两点间最长路为两点的差最小值。
注意如果不连通，则建一个源点，让它们强行联通。
题意：给出n个区间和每个区间内最少的点数目，求至少放几个点满足要求。
解：令x为[0,x)之间有几个点，x=2,y=3,z=5连边：(2,3+1,5)。
这里的点比较分散，源点不好建立，那就所有点之间都连边。
相邻两点之间：0<=xi+1-xi<=1，但这题里以大于等于为主，于是变个号。
还有，memset只能初始化0-255之间的值，WA在这好几次呜呜呜呜呜呜。
代码：
1 #include <stdio.h> 2 #include <algorithm> 3 #include <queue> 4 using namespace std; 5 #define maxx 1000005 6 #define inf 1e8+10 7 #define ll long long 8 int n; 9 struct edge{ 10 int u,v,w; 11 int nxt; 12 }e[maxx*2]; 13 int cnt=0,head[maxx]={0}; 14 int vis[maxx]={0},dis[maxx]={0}; 15 int maxn=-inf,minn=inf; 16 void add(int u,int v,int w){ 17 e[++cnt].u=u; 18 e[cnt].v=v; 19 e[cnt].w=w; 20 e[cnt].nxt=head[u]; 21 head[u]=cnt; 22 } 23 int spfa(int x){ 24 memset(dis,-0xf,sizeof dis); 25 queue<int> q; 26 dis[x]=0; 27 q.push(x); 28 while(!q.empty()){ 29 int now=q.front(); 30 q.pop(); 31 vis[now]=0; 32 for(int i=head[now];i;i=e[i].nxt){ 33 int to=e[i].v; 34 int temp=dis[now]+e[i].w; 35 if(temp>dis[to]){ 36 dis[to]=temp; 37 if(!vis[to]) { 38 q.push(to); 39 vis[to] = 1; 40 } 41 } 42 } 43 } 44 return dis[maxn+1]; 45 } 46 signed main(){ 47 scanf("%d",&n); 48 for(int i=0;i<n;i++){ 49 int x,y,z; 50 scanf("%d%d%d",&x,&y,&z); 51 add(x,y+1,z); 52 maxn=max(maxn,y); 53 minn=min(minn,x); 54 } 55 for(int i=minn;i<=maxn;i++) { 56 add(i, i + 1, 0); 57 } 58 printf("%d\n",spfa(minn)); 59 return 0; 60 }
