gym103371 B. Cilantro

题意：

　　有的面条带香菜，有的不带。现在给出做面条带不带香菜的顺序和每个顾客的需求，问第一个顾客可能拿到面条的下标和。

　　我真觉得香菜很好吃啊。

　　也就是给定两个由N和Y组成的序列S和T，长为n。将S放入栈中，以T的顺序取出，求T[0]在S中可能的下标之和。

解：

　　1.当S和T中N与Y的数目相等时一定可以通过出栈入栈使S和T相同。

　　证明：数学归纳法。当n=1时，显然成立。假设n=k时S能以T的顺序出栈，设n=k+1时S[k+1]=N，T[m]=N，那么N入栈，T[1,m-1]按之前顺序出栈，N出栈，　　　　　　T[m+1,k+1]按之前顺序出栈，符合要求。证毕。

　　2.如果T[0]对应S[m]，那么T[0]也可以对应m之前与T[0]相同的字母。

　　（口胡的）证明：每次把最靠前的满足需求的S给T一定可行。m越大，固定下来的顺序越多，能满足当前顺序的一定可以满足自由度更大的顺序。（听起来不太像人话的样子

　　也就是说，匹配具有单调性，我们想要T[0]尽量与S中靠后的字母匹配，枚举T[0]对应的位置，再判断是否可行，产生了一个nlogn的二分算法，很遗憾过不去。转换思路，将第一份食物尽量给后面的顾客，那么第一个顾客就能拿到尽量靠后的食物。假设将第一份食物给第k个顾客，也就是放在栈底，那么S[2,k]与T[1,k-1]要能匹配上。预先统计前缀和，这样可以O(1)验证。接着匹配第二份食物，直到一份食物只剩下第一个顾客这个选择，也就是他能拿到的下标最大的食物。

 

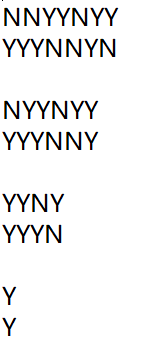
　　就像这样。

　　我太菜了只能用递归写，写完看了看别人的代码，好优雅%%%

　　代码：

　　

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define maxx 5000005
#define ull unsigned long long
//#define int long long
char s[maxx],c[maxx];
int s1[maxx]={0},t1[maxx]={0};
int n;
int st=1;
void ser(int l,int r,int L,int R){
    if(L>=R){
        st=l;
        return;
    }
    while(1){
        while(s[l]!=c[R])
            R--,r--;
        int t11=s1[r]-s1[l],t22=t1[R-1]-t1[L-1];
        if(s1[r]-s1[l]==t1[R-1]-t1[L-1]) {
            ser(l + 1, r, L, R - 1);
            break;
        }
        else
            R--,r--;
    }
}
signed main(){
//    int t;
//    scanf("%d",&t);
//    while(t--){
//
//    }

    scanf("%d",&n);
    scanf("%s%s",s+1,c+1);
    for(int i=1;i<=n;i++){
        s1[i]=s1[i-1]+(s[i]=='Y');
        t1[i]=t1[i-1]+(c[i]=='Y');
    }
    if(s1[n]!=t1[n]){
        printf("0\n");
        return 0;
    }
    ser(1,n,1,n);
    ll ans=0;
    for(int i=1;i<=st;i++)
        if(s[i]==c[1])
            ans+=i;
    printf("%lld\n",ans);
    return 0;
}

 

 

 

　　

推荐搭配食用bgm：歌に形はないけれど