从狭义相对论洛伦兹变换到广义相对论场方程的推导
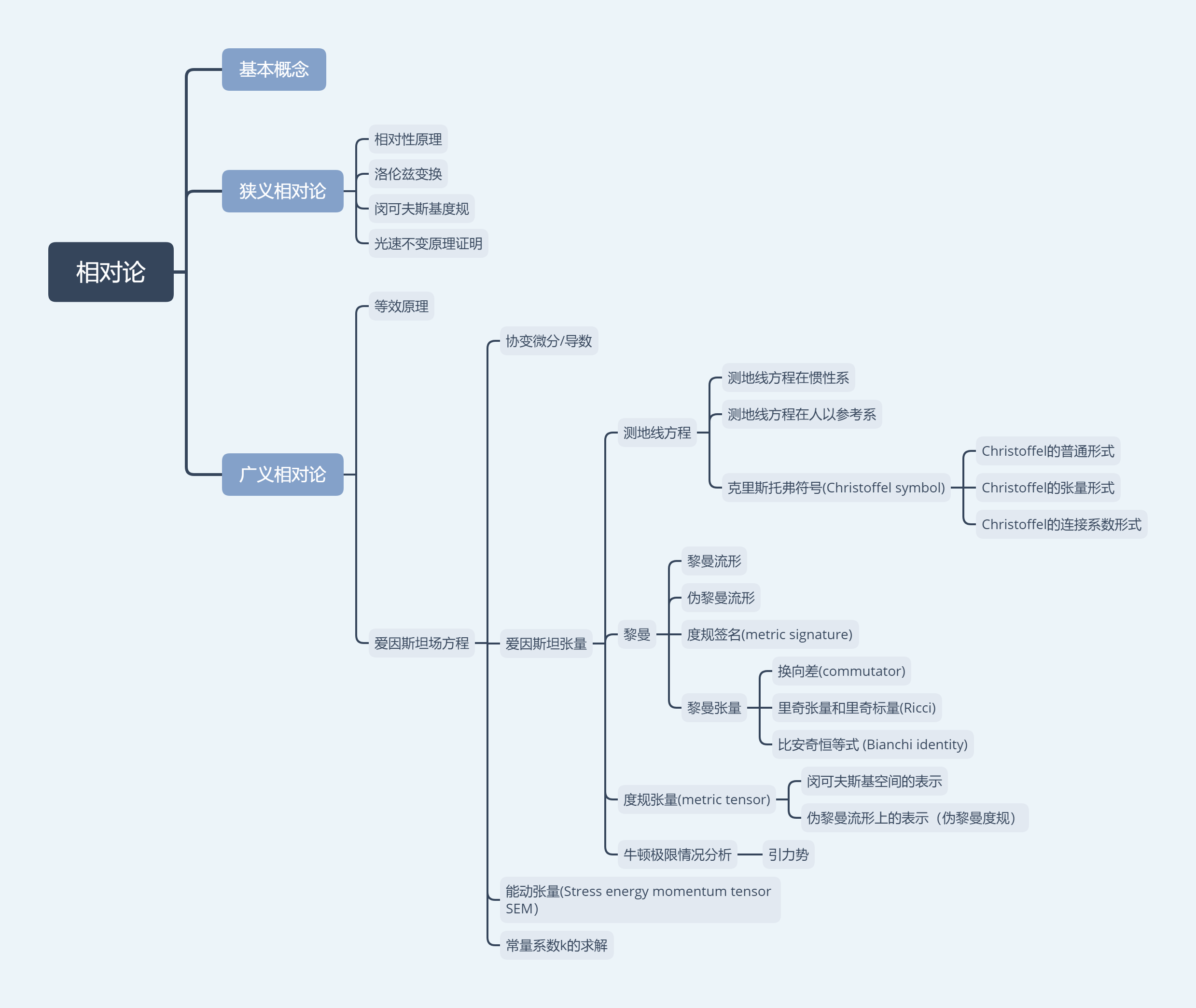
| 空间类型 | 空间曲率 | 平行线 | 三角形三内角之和 | 圆周率 | 例子 |
|---|---|---|---|---|---|
| 黎氏空间 | 正 | 无 | >180° | <π | 球面 |
| 欧式空间 | 零 | 一条 | =180° | =π | 平面 |
| 罗氏空间 | 负 | 无 | >=两条以上 | >π | 伪球面,马鞍面 |
我们称这个符号为dummy index
$$ 连续出现两次相同的符号,不强调他们是上标还是下标,都是满足爱因斯坦取和原则的 $$$$- 只出现一次的称为自由索引 $$$$- 但是注意不会出现三个相同的标记在同一项中 $$$$如x_{ii} \cdot y_{ji} 但是x_{ii}+y_{ji}却是可以的 $$$$- 当同时出现上下标时,也表示他们的取和如 x^i_j = \sum_{i,j}x^i_j $$$$- 一个等式两边的自由索引和虚拟索引个数应该一致 $$
洛伦兹变换的推导
假设最简单的线性变换, (t,x,y,z)代表s系,另外的一个代表s', 其他情况更复杂的情况都可以从基本情况推出来 $$ \begin{cases} t'=\alpha t + \beta x \\\\ x'=\gamma t + \sigma x \\\\ y'=y\\\\ z'=z\\\\ \end{cases} $$
$$这里的\alpha,\beta,γ和\sigma 都只依赖于v,如果 x=vt,则 x′ = 0$$
因为相对我s系是vt,就说明我是起点,因为是匀速直线运动 代入第二个式子得
$$x' = \sigma (v)⋅(x−vt ) ①$$
$$相对另一物体速度为0时,说明x=x^′,则此时\sigma =1 ,即\sigma (0)=1$$
$$根据相对性原理,s观察s'的相对速度是-v,代入 x = \sigma (−v)(x^′+vt^′ ) ②$$
$$由2式可得 : \frac{x−\sigma x^′}{\sigma v}= t' $$
$$将1式代入2式可得 (\frac{1}{\sigma v}−\frac{\sigma }{v})x+\sigma t=t^{'} ③式$$
$$将该式与方程组中第一个方程对比,可得 \sigma =\alpha$$
$$再由四维时空中两点的间隔对于两种参照系下相等:$$
$$ t^′2−x^′2= t^2−x^2 $$
代入特殊点 x = vt, x' = 0 有:
$$(\frac{x−\sigma x}{\sigma v})^2+0 =−t^2+x^2$$
$$两边同除以t得:\frac{1}{\sigma} =−1+v^2 即\sigma =\frac{1}{\sqrt{1−v^2 }}$$
$$将\sigma 代入③式可得\beta=0$$
于是得到洛伦兹坐标变换公式:
$$ \begin{cases} t'=t- \frac{\frac{v^2}{c^2} x}{\sqrt{\frac{1-v^2}{c^2}}}\\\\ x'=\frac{x-vt}{\sqrt{\frac{1-v^2}{c^2}}}\\\\ y'=y\\\\ z'=z\\\\ \end{cases} $$
对时间乘因子ic,c是具有速度量纲的常数,ict就是具有长度量纲的一个虚数了,将ict第四维度,规定坐标变换时,变换矩阵必须正交,用来保证任意两点的距离不变,比如洛伦兹变换: $$t^′= \frac{\frac{t− vx}{c^2} }{\sqrt{1−(\frac{v}{c})^2 } }$$
通过洛伦兹变换就可以解释 钟慢效应,尺短效应等高速运动物体物理特性发生的差异,这里不再详细解释。
洛伦兹变换的矩阵形式 $$如果把x,y,z依次记为x_1, x_2 , x_3 ,记ict为x^4,写成矩阵形式就是: $$$$ \begin{pmatrix}x_1'\\\\ x_2'\\\\x_3'\\\\x_4' \end{pmatrix}= \begin{pmatrix} \gamma & 0 & 0 & i\beta\gamma \\\\ 0 & 1 & 0 & 0 \\\\ 0 & 0 & 1 & 0 \\\\ -i\beta\gamma & 0 & 0 & \gamma \\\\ \end{pmatrix} \begin{pmatrix}x_1\\\\ x_2\\\\x_3\\\\x_4 \end{pmatrix} $$ $$ 上式中 \beta = \frac{v}{c} , \gamma =\frac{1}{\sqrt{1-(\frac{v}{c})}} $$$$ $$此时 s^2=x_1^2+x_2^2+x_3^2+x_4^2=r^2+(ict)^2 $$ $$注意这里说的x是\Delta x,即物体的距离s^2= r^2−(ct)^2$$ $$s就是四维时空两点中的间隔, 为了后面统一表述这里将s^2 替换成 ds^2 $$ $$他们并没有什么差别,d是距离而不是微分, 将ds^2 表示成矩阵相乘的形式 $$ $$ ds^2 = \begin{pmatrix}-1 & & &\\\\ & 1 & & \\\\ & & 1 &\\\\& & & 1 \end{pmatrix} \begin{pmatrix}c^2t^2\\\\ x_2^2\\\\x_3^2\\\\x_4^2 \end{pmatrix}=\eta⋅(c^2 t^2, x_1^2,x_2^2,x_3^2 ) $$ $$ 其中 \eta_{\alpha\beta}=diag(−1,1,1,1),这里 \eta_{\alpha\beta} 对角线有三正一负,$$ $$这里的系数矩阵称为\eta,也被称为闵可夫斯基度量(度规), 那么距离也可以表示成 $$ $$ds^2= \sum_{\mu=0}^3\sum_{\nu=0}^3\eta_{\mu\nu} x^\mu x^\nu$$ $$如果用爱因斯坦取和标记表示 ds^2=\eta_{\mu\nu} x^\mu x^\nu (\mu、\nu为矩阵的行和列的取值)$$ $$在闵可夫斯基空间V中的适合 s^2=0的x称为类光向量或者零矢量,$$ $$ 或称x是类光的(lightlike)(因为此时空间距离x^2=(ict)^2 ),$$ $$V中适合 \eta(x,x)>0的向量 x 成为类空向量或称x是类空的(spacelike ),$$ $$适合\eta(x,x)\lt 0 的向量x称为类时向量或称x是类时的(timelike) , $$$$闵可夫斯基空间中所有零矢量的集合构成了该时间所有事件的光锥$$
流形是局部具有欧几里得空间性质的空间,流形的定义体现了坐标系是局部的,并限制了这些局部范围内坐标允许的变换, 一个表面是一个二维流形,时空是一个四维流形,经典力学空间和广义相对论所用时空都是流形,$$黎曼流形具有正定的量度,即 ds^2 始终为正$$

5. 度规张量($g_{\mu\nu}$):
我们命名时空时空坐标$$\xi^\alpha 即 \xi^0=CT,\xi^1=Y, \xi^2=Y,\xi^3=Z $$ 我们继续表述在新参考系下坐标进行微分: $$d\xi^\alpha =\frac{\partial \xi^\alpha }{\partial x^0 }dx^0+\frac{\partial \xi^\alpha }{\partial x^1 } dx^1+\frac{\partial \xi^\alpha }{\partial x^2 } dx^2+\frac{\partial \xi^\alpha}{\partial x^3} dx^3 $$$$ d\xi^\alpha = \frac{\partial \xi^\alpha}{\partial x^\mu} dx^\mu,d\xi^\beta= \frac{\partial \xi^\beta}{\partial x^ \nu} dx^\nu $$ $$那么 ds^2=\eta_{\alpha \beta} \frac{\partial \xi^\alpha}{\partial x^\mu} \frac{\partial \xi^\beta}{\partial x^ \nu} dx^\nu dx^\mu =g_{\mu\nu} dx^ \nu dx^\mu $$ $$其中 g_{\mu\nu} = \eta_{\alpha \beta} \frac{\partial \xi^\alpha }{\partial x^\mu } \frac{\partial \xi^\beta}{\partial x^\nu } $$ $$ 可以看到g_{\mu\nu}=g_{\nu\mu},因为\eta是一个对角矩阵 $$ $$ 我们将g的逆表示成 g^{\mu\alpha} $$ $$ g^{\mu\alpha} g_{\alpha\nu}=(\eta_{\gamma\beta} \frac{\partial \xi^\gamma}{\partial x^\alpha} \frac{\partial \xi^\beta}{\partial x^\mu })^{-1}⋅ (\eta_{\gamma\beta} \frac{\partial \xi^\gamma}{\partial x^\alpha} \frac{\partial \xi^\beta}{\partial x^\nu }) $$$$=\frac{\partial \xi^\beta}{\partial x^\mu }^{-1}⋅\frac{\partial \xi^\gamma}{\partial x^\alpha }^{-1}⋅\eta_{\gamma\beta}^{-1}⋅ \eta_{\gamma\beta}⋅\frac{\partial \xi^\gamma}{\partial x^\alpha } \frac{\partial \xi^\beta}{\partial x^\nu} = \delta_\nu^\mu (Kronecker delta) $$ $$ 上面这个表示和结果非常重要,后面也要用到 g_{\mu\nu} 非常重要就在于 $$$$ 它包含了所有关于时空和引力场的信息,g_{\mu\nu}一共有16个项$$$$ 但是由于对称的原因合并下来只有10个项就是上三角或下三角那10个 $$

6. 测地线方程:
对等效原则的考虑,如果我们要描述一个物体在地球引力场中运动,必须遵循以下步骤: $$ 1.用局部惯性自由落体参考系来描述运动 $$ $$ 2.对局部惯性参考系进行变换,变换到大地参考系 $$ $$ 1.用自由落体参考系来描述运动 $$ $$ 在自由下落的参考系中,我们命名时空坐标为\xi^\alpha ,其中\alpha \in {0,1,2,3} $$ $$ \frac{d^2 \xi^\alpha}{d\tau ^2}=0 , ds^2=cd\tau ^2 $$$$ (\because t' = \frac{t − \frac{v^2}{c^2} x}{\sqrt{\frac{1−v^2}{c^2}}} \therefore dt' = cdt \Rightarrow ds^2=cd\tau ^2) $$ $$ 这里\tau 值得是在静止参考系中观察者测量的时间,也称为固有时间 $$ $$ 2.在大地参考系中描述运动(向上加速) $$ $$ 令x^\mu 是任意非惯性参考系的各轴 $$ $$ 有: \frac{d\xi^\alpha }{d\tau} =\frac{\partial \xi^\alpha }{\partial x^\mu} \frac{dx^\mu}{d\tau} $$ $$ 这就是爱因斯坦取和标记: 对于上式实际上为 \frac{d\xi^\alpha }{d\tau} =\sum_{i=0}^{3}\frac{\partial \xi^\alpha }{\partial x^i} \frac{dx^i}{d\tau} $$ $$ 将链式法则运用到自由落体方程中有: $$ $$ 0 = \frac{d}{d\tau} (\frac{d\xi^\alpha }{d\tau}) =\frac{d}{d\tau}( \frac{\partial \xi^\alpha }{\partial x^\mu } \frac{dx^\mu}{d\tau}) $$ $$ = \frac{d}{d\tau} (\frac{\partial \xi^\alpha }{\partial x^\mu }) \frac{dx^\mu}{d\tau} +\frac{\partial \xi^\alpha}{\partial x^\mu } \frac{d^2 x^\mu}{d\tau ^2 } $$ $$ = \frac{d}{d\tau} (\frac{\partial \xi^\alpha }{\partial x^\mu }) \frac{dx^u}{dx^\nu } \frac{dx^ \nu}{d\tau} +\frac{\partial \xi^\alpha}{\partial x^\mu } \frac{d^2 x^\mu}{d\tau ^2 } $$ $$ = \frac{dx^\nu}{d\tau} (\frac{\partial \xi^\alpha}{\partial x^\mu \partial x^ \nu }) \frac{dx^\mu}{d\tau} +\frac{\partial \xi^\alpha }{\partial x^\mu } \frac{d^2 x^\mu}{d\tau ^2 } $$ $$ 两边同时乘\frac{\partial x^\beta}{\partial \xi^\alpha} 得: $$ $$ 0 = \frac{\partial x^\beta}{\partial \xi^\alpha } \frac{dx^\nu}{d\tau} (\frac{\partial \xi^\alpha}{\partial x^\mu \partial x^ \nu }) \frac{dx^\mu}{d\tau} +\frac{\partial \xi^\alpha }{\partial x^\mu} \frac{d^2 x^\mu}{d\tau ^2 } \frac{\partial x^\beta}{\partial \xi^\alpha} $$ $$ 令\frac{\partial x^\alpha }{\partial x^\mu }=\delta_\mu^\beta (Kronecker delta 克罗内科函数, $$$$即如果\beta和\mu一致值为1,不一样则值为0 ) 带入可得: $$ $$ 0 = \frac{\partial x^\beta}{\partial \xi^\alpha} \frac{dx^\nu}{d\tau} \frac{\partial \xi^\alpha }{\partial x^\mu \partial x^ \nu } \frac{dx^\mu}{d\tau} +\delta_\mu^\beta \frac{d^2 x^\mu}{d\tau ^2 } 因为只有相等时为1,所以可以用\beta代替\mu ,即 $$$$ 0 = \frac{\partial x^\beta}{\partial \xi^\alpha} \frac{dx^\nu}{d\tau} \frac{\partial \xi^\alpha }{\partial x^\mu \partial x^ \nu } \frac{dx^\mu}{d\tau} +\frac{d^2 x^\beta}{d\tau ^2 } $$ $$ 最终: 0 = \frac{d^2 x^\beta}{d\tau ^2 }+\Gamma_{\mu \nu}^\beta \frac{\partial x^\mu}{\partial\tau} \frac{\partial x^ \nu}{\partial \tau} (测地线方程Geodesic equation) $$ $$ 其中 \Gamma_{\mu \nu}^\beta= \frac{\partial x^\beta}{\partial \xi^\alpha} \frac{\partial \xi^\alpha}{\partial x^\mu \partial x^ \nu } (Christoffel symbol) $$ $$ 上式被称为测地线方程 $$ $$ 通过方程可知: $$ $$ 1. 在加速的参考系下,粒子的运动不再是直线运动了,因为某种惯性力施加在它上面: $$$$f^\beta=−m \Gamma_{\mu \nu}^\beta \frac{\partial x^\mu}{\partial \tau } \frac{\partial x^ \nu}{\partial \tau} $$$$ 上述环境如果实在重力场中进行自由落体,那么惯性力就是重力了, $$$$ 如果我们知道christoffel符号的组成部分,我们就可以确定上述中物体的运动速度了。 $$$$ - 这个等式将直线运动推广到了弯曲的时空中,等会我们会介绍如按照度量张量 $$$$看到从时空度两种计算christoffel符号 $$$$ - 该方程实际上代表10项的4个不同方程\beta从0到3, \mu和 \nu 的组合$$$$会有16种,但其中有些对称 所以只有10个 $$$$- 在同一个测地线方程中,我们将在牛顿极限测地线方程中演示如何在$$$$特定条件下推导张量和重力之间的直接关系。 $$

8.Christoffel张量

9.Christoffel符号2(连接系数)

10. 协变导数:
在微分几何里,人们希望推广这个概念到一般微分流形上。首先求导(或求微)的对象从函数推广到向量场(就是向量丛的截面,如切向量场和余切向量场), 定义域则移到了整个流形上(不再是平坦的空间), 求导的方向可以是任何切向量的方向。 这样得到的导数就称为协变导数,其微分称为协变微分。
向量的协变微分
$$ 对于一个向量V = V^\alpha e_{\alpha} 其对x^{\beta} 求偏导 为:\frac{ \partial V}{\partial x^\beta }=\frac{\partial V^\alpha }{\partial x^\beta} e_\alpha +V^{\alpha} \frac{\partial e_\alpha }{\partial x^\beta } $$$$ 之前我们得到连接系数为: \Gamma_{\alpha \beta}^\gamma (e_\gamma ) = \frac{\partial e_{\alpha} }{\partial x^\beta } $$$$ 将其带入上式可得: \frac{\partial V}{\partial x^\beta} =\frac{\partial V^\alpha }{\partial x^\beta } e_\alpha +V^\alpha \Gamma_{\alpha \beta}^\gamma e_\gamma $$$$ 等式的右侧有两个虚拟符号\alpha 和\gamma ,交换他们 (为什么能交换) $$$$ \frac{\partial V}{\partial x^\beta}=\frac{\partial V^\alpha }{\partial x^\beta} e_\alpha +V^\gamma \Gamma_{\gamma\beta}^\alpha e_\alpha , 提出e_\alpha $$$$ \frac{\partial V}{\partial x^\beta}=(\frac{\partial V^\alpha }{ \partial x^\beta } +V^\gamma \Gamma_{\gamma\beta}^\alpha )e_\alpha $$$$ 此表达式表示V在x的\beta方向上的变化率 $$$$ 可以用 \nabla来表示 协变导数值: $$$$\nabla_\beta V^\alpha =\frac{\partial V^\alpha }{ \partial x^\beta } +V^\gamma \Gamma_{\gamma\beta}^\alpha $$$$ \nabla_\beta V^\alpha 的等价符号是 D_\beta V^\alpha 和 V_{;\beta}^\alpha $$$$ 备注: $$$$ - 度规张量的偏导数消失在M的任何点等价于Christoffel符号的消失, $$$$这样我们可以在任何惯性或局部惯性狂阿基背景下重写整个基本等式: $$$$\nabla_\beta V^\alpha =\frac{\partial V^{\alpha} }{\partial x^\beta } $$$$ - Christoffel符号本身不会转换成张量是因为,总可以找到令Christoffel为0 $$$$ 的局部惯性系,但对于张量却不会。 $$$$ 此外还可以推导出协变向量的协变微分。 由于此等式对于每个任意A向量都成立,$$$$因此方括号中的数量必须为null。因此,我们证明了向量B的协变分量的$$$$协变导数的表达式如下: $$$$ \nabla_\alpha B_\mu = \frac{\partial B_\mu}{\partial x^\alpha} - B_\sigma \Gamma^\sigma_{\alpha \mu} $$$$ 其中B为协变向量 $$
11. 黎曼张量
换向差(commutator):表示一个操作整箱和方向的差异如:[AB] = AB-BA ,如果更改顺序后没有影响,则换向差为0 ,因为在平坦的空间求协变微分操作先后都一样将换向差应用于协变微分的任何非零结果都可以归因与空间的曲率,从而归因于黎曼张量, 黎曼张量实际上衡量了时空的曲率
$$ 我们通过计算协变微分的换向差(commutation)\nabla_c \nabla_b V_\alpha −\nabla_b \nabla_c V_\sigma $$$$来推导黎曼张量 或者用分号表示:V_{\alpha ;bc} −V_{\alpha ;cb} $$$$ 前面推导的协变微分为:\nabla_b V_\alpha =\partial _b V_\alpha −\Gamma_{ab}^d V_d $$$$ 于是: \nabla_c \nabla_b V_\alpha = \partial _c (\nabla_b V_\alpha )−\Gamma_{\alpha c}^e \nabla_b V_e −\Gamma_{bc}^e \nabla_e V_\sigma $$$$ 其中右侧第一项:\partial _c (\nabla_b V_\alpha )=\partial _c \partial _b V_\alpha −\partial _c (\Gamma_{ab}^d V_d ) $$$$ \partial _c (\nabla_b V_\alpha )=\partial _c \partial _b V_\alpha −\partial _c (\Gamma_{ab}^d ) V_d−\partial _c \Gamma_{ab}^d (V_d ) $$$$ 右二\Gamma_{ac}^e \nabla_b V_e=\Gamma_{ac}^e (\partial _b V_e −\Gamma_{be}^d V_d) $$$$ 右三\Gamma_{bc}^e \nabla_e V_\alpha =\Gamma_{bc}^e (\partial _e V_\alpha −\Gamma_{\alpha e}^d V_d ) $$$$ 带入公式可得\nabla_c \nabla_b V_\alpha = $$$$\partial _c \partial _b V_\alpha - \partial _c (\Gamma_{ab}^d ) V_d −\partial _c (V_d ) \Gamma_{ab}^d −\Gamma_{ac}^e (\partial _b V_e−\Gamma_{be}^d V_d )−\Gamma_{bc}^e (\partial _e V_\alpha −\Gamma_{ae}^d V_d ) $$$$ 然后交换bc可得\nabla_b \nabla_c V_\alpha $$$$ = \partial _b \partial _c V_\alpha - \partial _b (\Gamma_{ac}^d ) V_d −\partial _c (V_d ) \Gamma_{ac}^d −\Gamma_{ac}^e (\partial _c V_e−\Gamma_{ce}^d V_d )−\Gamma_{cb}^e (\partial _e V_\alpha −\Gamma_{ae}^d V_d ) $$$$ 计算\nabla_c \nabla_b V_\alpha −\nabla_b \nabla_c V_\alpha $$$$ = - \partial _c (\Gamma_{ab}^d ) V_d −\partial _c (V_d ) \Gamma_{ac}^d −\Gamma_{ac}^e (\partial _c V_e−\Gamma_{ce}^d V_d )−\Gamma_{cb}^e (\partial _e V_\alpha −\Gamma_{ae}^d V_d ) $$$$ 展开: \nabla_c \nabla_b V_\alpha − \nabla_b \nabla_c V_\alpha $$$$ = −\alpha _c (\Gamma_{ab}^d ) V_d −\alpha _c (V_d ) \Gamma_{ab}^d − \Gamma_{ac}^e \partial _b V_e+\Gamma_{ac}^e \Gamma_{be}^d V_d+\partial _b (r_ac^d ) V_d+\partial _b (V_d ) \Gamma_{ac}^d+\Gamma_{ab}^e \partial _c V_e+\Gamma_{ce}^d V_d $$$$ = \partial _b (V_d ) \Gamma_{ac}^d −\partial _c (V_d ) \Gamma_{ab}^d+\Gamma_{ab}^e \partial _c V_e −\Gamma_{ac}^e \partial _b V_e+(\partial _b (\Gamma_{ab}^d )−\partial _c (\Gamma_{ab}^d )+\Gamma_{ac}^e \Gamma_{be}^d −\Gamma_{ab}^e \Gamma_{ce}^d ) V_d $$$$ 前面我们计算出Christoffel的另一种表示\Gamma_{\alpha \beta}^\Gamma e_\gamma = \frac{\partial (e_{\alpha } )}{\partial x^\beta } $$$$ 因此: \Gamma_{ab}^e \partial _c V_e − \Gamma_{ac}^e \partial _b V_e= \partial _c \Gamma_{ab}^e V_e −\partial _b \Gamma_{ac}^e V_e (偏导顺序无关)$$$$ =\partial _c \partial _b V_a−\partial _b \partial _c V_\alpha =0 $$$$ 通过交换b,c 可以得到: \partial _b (V_d ) \Gamma_{ac}^d −\partial _c (V_d ) \Gamma_{ab}^d=0 $$$$ 最后,commutation为: $$$$ \nabla_c \nabla_b V_\alpha − \nabla_b \nabla_c V_\alpha =(\partial _b (\Gamma_{ac}^d ) −\partial _c (\Gamma_{ab}^d )+\Gamma_{ac}^e \Gamma_{be}^b −\Gamma_{ab}^e \Gamma_{ce}^d ) V_d=R_{abc}^d V_d $$$$ 将R_{abc}^d 称为黎曼张量。 $$$$ 简化表示成:R_{abc}^d= \Gamma_{ac,b}^d −\Gamma_{ab,c}^d+\Gamma_{ac}^e \Gamma_{be}^d −\Gamma_{ab}^e \Gamma_{ce}^d $$$$ 因为有4个索引,所以 每个索引有4种取值,所以一种有4^4=256个项 $$

12.张量收缩
坐标系变换
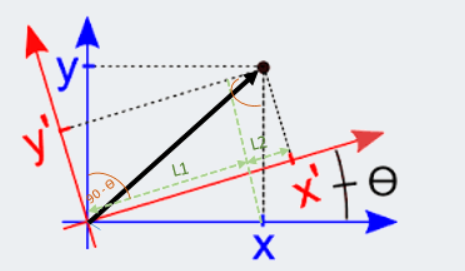
$$对坐标系旋转\theta 可以得到新的坐标系,则向量A在两个坐标系下的坐标分别为: $$$$ A=A^x e_x+A^y e_y $$$$ A=A^′x e_x+a^′y e_y $$$$ 其中A^{′x}=L_1+L_2 $$$$ L_1=A^x cos(\theta ) $$$$ L_2=A^y cos(\pi/2−\theta ) $$$$ 则(A^′)^x= A^x cos(\theta )+A^y cos(\pi/2−\theta ) $$$$ 同理 A^′y= A^x cos(\pi/2+\theta )+A^y cos(\theta ) $$$$ 则A'就可以表示成矩阵的乘法: $$$$ \begin{pmatrix} A^{'}_{x} \\\\ A^{'}_{y} \end{pmatrix} = \begin{pmatrix} cos(\theta) & sin(\theta) \\\\ -sin(\theta) & cos(\theta) \end{pmatrix} \begin{pmatrix}A^{x}\\\\ A^{y} \end{pmatrix} $$
基向量变换
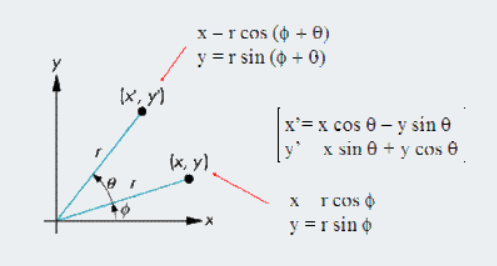
$$在新的基向量上表示旋转后的向量,对于向量逆时针旋转\theta 相当于顺时针将坐标系旋转\theta $$ $$ \begin{pmatrix} A^{'}_{x} \\\\ A^{'}_{y} \end{pmatrix} = \begin{pmatrix} cos(\theta) & -sin(\theta) \\\\ sin(\theta) & cos(\theta) \end{pmatrix} \begin{pmatrix}A^{x}\\\\ A^{y} \end{pmatrix} $$$$ dx^{′1}=(\partial x^{′1})/(\partial x^{1} ) dx^1+(\partial x^{′1})/(\partial x^2 ) dx^2 $$$$ dx^{′2}=(\partial x^{′2})/(\partial x^1 ) dx^1+(\partial x^{′2})/(\partial x^2 ) dx^2 $$$$ dx^{'i}=\frac{\partial x^{'i}}{\partial x^j} dx^j $$$$ 计算适当的导数我们得到: $$$$ \frac{\partial x^{'1}}{\partial x^1} = cos\theta \qquad \frac{\partial x^{'2}}{\partial x^1} = sin \theta $$$$ \frac{\partial x^{'1}}{\partial x^2} = -rsin\theta \qquad \frac{\partial x^{'2}}{\partial x^2} = rcos\theta $$$$ 因为dx^{'1}和d^{'2}实际上反映了e_1 和e_2 的大小所以: $$$$ e_1 = \frac{\partial x^{'1}}{\partial x^1} \vec{i} +\frac{\partial x^{'2}}{\partial x^1} \vec{j} = cos \theta \vec{i}+\ sin\theta vec{j} e_2 = \frac{\partial x^{'1}}{\partial x^2} \vec{i} +\frac{\partial x^{'2}}{\partial x^2} \vec{j} = -rsin\theta \vec{i} + rcos\theta \vec{j} $$$$这样我们就得到了分量A^{'i}的定义,又称为逆变(反变或contravariant)分量 $$$$ A^{'i} = \frac{\partial x^{'i}}{\partial x^j} A^j $$
协变分量和逆变分量
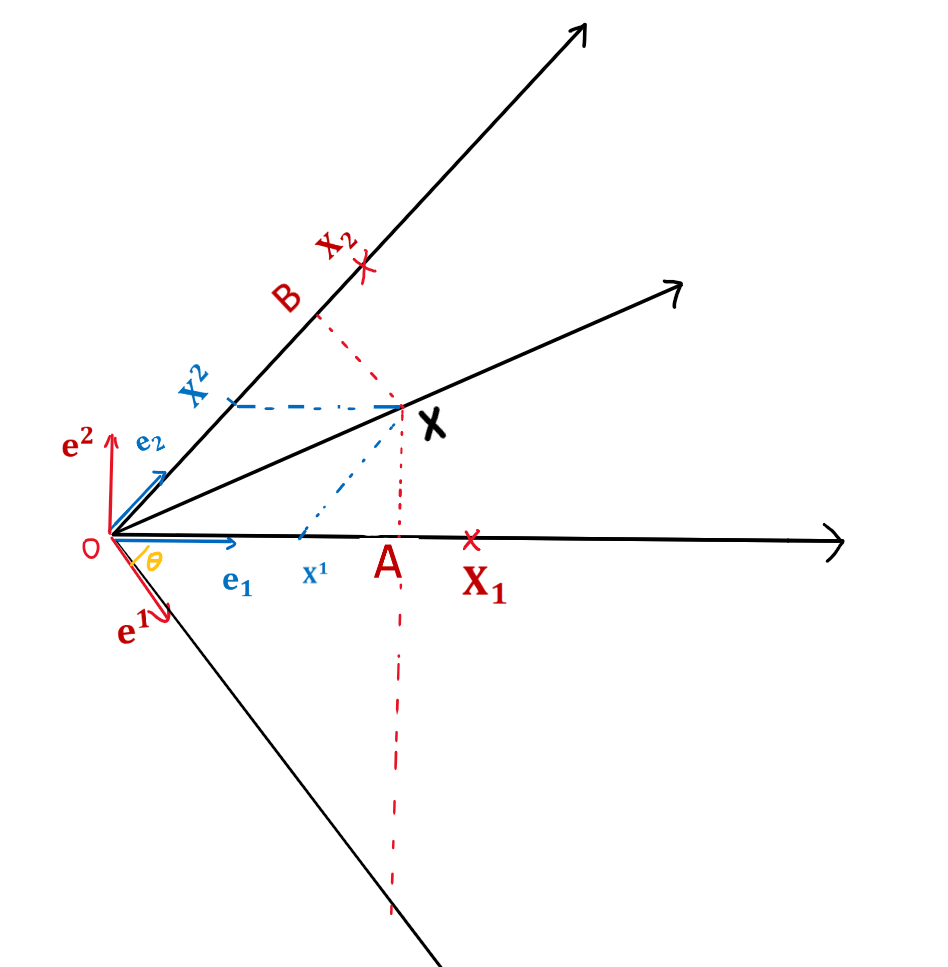
$$ 图中 X = e_1 x^1+e_2 x^2 $$$$ 我们构造了e_1 和 e_2 的对偶向量e^1 和 e^2,我们希望用对偶向量表示原向量X $$$$ 我们令 协变分量为 x_1= e_1 x ,注意协变分量是标量 $$$$ 我们期望的结果是: X = e^1 X_1+e^2 X_2 $$$$ 对偶向量是对于e^i满足\lt e^i,e_j \gt =\delta_j^i 的向量e^j $$$$ 举个例子:e^1 是 e_1 的对偶向量,他满足 e^1 \cdot e_1=1 $$$$ 即对偶空间的相同下标的基向量内积为1, 关于对偶空间和对偶基可以看: $$ https://blog.csdn.net/sumx2015/article/details/78909635 解释的很形象了 $$ 对偶基的要求还蕴含了任意非相同标记的基向量和对偶基向量内积为0,就是说他们垂直 $$$$ 下面我们来证明为什么这样的向量可以构造出来新的基底 $$$$ 由图根据平行四边形法则我们可知: $$$$ |x|sin\theta =|e^1 x_1 |cos\theta $$$$ sin\theta =\frac{|e^1 (e_1 x)|}{|x|} cos\theta $$$$ sin\theta =\frac{|e^1 | e_1 |cos(\pi/2−\theta ) |}{|x|} cos\theta $$$$ 1 = |e^1| |e_1|cos\theta $$$$ 即e^1 e_1=1 , 同理可以证明e^2 e_2=1 $$$$ 反过来 也可以推导出 |x|sin\theta =|e^1 x_1 |cos\theta $$$$ 所以\lt e^i,e_j\gt =\delta_{j}^{i} 是满足协变分量为x_1= \lt e_1 ,x\gt 的原向量X在对偶空间上的表示 $$$$ 尤其是当 e_1=1时,A点就和 X_1 重合了,此时X_1 就是x在 e_1 轴上的投影 $$$$ 对于逆变分量, 如果改变基向量e_1 的大小,为了保证X= e则逆变分量X^1 的大小会反向改变, $$ 比如基向量减小 一半,逆变分量就会增加一倍, 而对于协变分量,如果原空间的基向量模增加一倍, 对偶空间的基向量模减小一倍,因为内积为1的约束, 对应协变分量就增加一倍,所以 协变指的是,随着原空间的基向量的变化而正相关变化 之前我们推导对于逆变张量的分量: $$ A^{'i} = \frac{\partial x^{'i}}{\partial x^{'i}} A^j $$$$ 同理对协变张量的分量效果也是一致的: $$$$ A_{'i} = \frac{\partial x^{'i}}{\partial x^{'i}} A_j $$
张量的缩放
当把上面的逆变张量和协变张量推广到普通情况就相当复杂: $$ 令原张量表示成: S_{j_1 j_2⋯j_q}^{i_1 i_2⋯i_p } $$$$ 则经过变换后的矩阵\bar{S}可以表示成: $$$$ \bar{S}_{j_1 j_2⋯j_q}^{i_1 i_2⋯i_p}= S_{\beta_1 \beta_2⋯\beta_q}^{\alpha_1 \alpha_2⋯\alpha_p}\frac{\partial \bar{x}^{i_1 }}{\partial x^{\alpha_1}} \frac{\partial \bar{x}^{i_2 }}{\partial x^{\alpha_2}}\cdots \frac{\partial \bar{x} ^{i_p }}{\partial x^{\alpha_p } } \frac{\partial \bar{x} ^ {\beta_1}}{\partial x^{j_1}} \frac{\partial \bar{x} ^{\beta_2}}{\partial x^{j_2 }}\cdots \frac{\partial \bar{x} ^{\beta_p }}{\partial x^{j_q }} $$$$ 当我们尝试让某个上标i_k 和某个下标j_b 相等时,就可以在右式中约去, $$$$ 反映到左式中就可以直接约去,我们把这种操作叫做contraction $$$$ 张量压缩,当然我们也可以进行扩张,制造两个相同的下标。 $$$$ 度量张量最有用的功能之一就是在其他张量的协变量和范变量分量之间进行转换 $$$$ 因为对 度规张量进行变换可以得到: $$$$ g_{\mu\nu} = \eta_{\alpha \beta} \frac{\partial \xi ^{\alpha}}{\partial x^\nu} \frac{\partial \xi ^\beta}{\partial x^\nu} $$$$ g^{'}_{\mu\nu} = \eta_{\alpha \beta} \frac{\partial \xi ^{\alpha}}{\partial x^{'\nu}} \frac{\partial \xi ^\beta}{\partial x^{'\nu}} = \eta_{\alpha \beta} \frac{\partial \xi ^ \alpha}{\partial x^\sigma}\frac{\partial x^\sigma}{\partial x^{'\mu}} \frac{\partial \xi^\beta}{\partial x^\rho} \frac{\partial x^\rho}{\partial x^{'\nu}} $$$$ g^{'}_{\mu\nu} =\eta_{\alpha \beta} \frac{\partial \xi ^ \alpha}{\partial x^\sigma} \frac{\partial \xi^\beta}{\partial x^\rho} \frac{\partial x^\sigma}{\partial x^{'\mu}} \frac{\partial x^\rho}{\partial x^{'\nu}} $$$$ g^{'}_{\mu\nu} = g_{\sigma \rho}\frac{\partial x^\sigma}{\partial x^{'\mu} }\frac{\partial x^\rho}{\partial x^{'\nu}} $$$$ 之所以能够进行压缩,是因为度规张量恰好 $$$$ 需要对下标求偏导,如上面的压缩一样,对相同的标记进行了约分。 $$$$ 因此,给定张量的逆变分量和原始基向量,并希望确定协变分量, $$$$一种方法可能是确定对偶基向量, 如g_{ij} A^j=A_i ,g^{ij} A_i=A^j , g^{ij} A_i=A^j $$

13.Ricci张量和Ricci标量

14. 能动张量:
$$ 应力能量动量张量(Stress \quad energy \quad momentum \quad tensor,SEM):T^\alpha \beta $$$$ 简称能动张量,用来描述能量和动量在时空中的密度与通量(flux), $$$$其为牛顿物理中应力张量的推广,能动张量在广义相对论中是重力场的源, T^\alpha $$$$ \beta 给出四维动量或4-动量P(\frac{E}{c},p_x,p_y,p_z)之\alpha 分量$$$$(\alpha ,\beta依次代表1,2、、)通过一个坐标为常数x^b 表面的通量, $$$$ 另外要注意的是SEM 是对称的(当自旋张量为0时), 即T^{ab}=T^{ba} $$$$ T^{00} 代表能量密度 , T^{0i} 代表能量通过x^i 表面的能量密度,$$$$等同于 T^{i0} 第i动量之动量密度,当\alpha \beta $$$$ 不同时表示剪应力,相同时表示正向应力。 $$$$ 由于我们最终的目标是在时空几何图形及其内容之间建立关系,$$$$因此我们首先必须找到用什么来描述,$$$$由于质量,能量和动量都相关(E^2=p^2 c^2+m_0^2 c^4), $$$$ 证明:p^2=(m_0 c)^2 , $$$$ p^2= \eta_u \nu p^\mu p^ \nu=\frac{E^2}{c^2} $$$$ −p_x^2−p_y^2−p_z^2=\frac{E^2}{c^2} −p^2⇒(m_0 c)^2=\frac{E^2}{c^2 −p^2}\Rightarrow E^2 = p^(2c^2 ) $$$$ 所以似乎假设: 广义相对论的引力场来源应该包括动量,能量和质量。 $$$$另一方面,用泊松方程( 泊松方程:\nabla^2 \phi=f ,就是各维的二阶偏导数之和, ) $$$$ 表示的描述由质量密度引起的重力的等效牛顿方程为: $$$$− \nabla g=−\nabla(−\nabla\phi)=4\pi G\rho $$$$ 那么能量密度是张量还是标量呢? $$$$ 先考虑相对静止的非相互作用例子相对于彼此的提及dxdydz,,也被称作 dust cloud $$$$ 在它自己的参考系,这个dust有自己的能量密度(质量密度) \rho _0=m_0 n_0 , $$$$在这里m_0 代表了尘粒的质量, n_0 $$$$ 代表了单位提及例子的数量,在洛伦兹变换下,会变成: $$$$ m_0 \Rightarrow m_0 \Gamma , n_0→n_0 \Gamma\Rightarrow \rho _0 \Rightarrow\rho =\rho _0 \Gamma^2 u^\mu=\Gamma(1,v) $$$$ =(\Gamma,v_x \Gamma, v_y \Gamma,v_z \Gamma)^T=(u^t,v_x u^t, v_y u^t,v_z u^t )^T $$$$ 所以设置\Gamma= u^t 使用这种相等性,并且每个粒子的能量等于p^t=mu^t,$$$$ 我们改写S'中的总能量密度: $$$$ \rho ≡np^t=(n_0 u^t )(mu^t )=(n_0 m) u^t u^t=\rho _0 u^t u^t $$$$ 可以将\rho 解释成对称的二维张量,也就是我们说的能动张量, T^{\mu \nu}=T^ \nu\mu=\rho _0 u^\mu u^ \nu $$$$ 上述可知T^{00} 可表示成能量密度 ,对于4x4的其他项来说: $$$$ T^tx=\rho _0 u^t u^x=(n_0 m) u^t u^x=(n_0 u^t )(mu^t ) v_x=np^t v_x=\frac{(nAv_x dt) p^t}{Adt} $$$$ 其中A_vx dt 代表了 在dt时间内垂直x方向穿过表面A的dust体积, $$$$ 可以表示通过该表面的颗粒总数, $$$$ 则T^tx=T^xt 除了T的第一行和第一列外,其他的部分我们表示成 $$$$ T^kl=\rho_0 u^k u^l=(n_0 m) u^k u^l=(n_0 m) u^t v_k u^l=(n_0 u^t ) v_k (mu^l )= $$$$nv_k (mu^l )=nv_k p^l=mv_k p^l=\frac{(nAv_k dt) p^l}{Adt} $$$$ 其中p^l 是动量,则T^{kl} 表示l动量在k方向的通量, $$

15.牛顿极限
牛顿极限: 是一种数学近似值,用于表示(1)弱引力(2)与光速相比运动缓慢的物体(3)缓慢改变引力场的物理系统,在这种情况下,牛顿万有引力定律可以用于获得准确的值, 在牛顿极限中,时空近似平坦,并且可以在有限距离内使用闵可夫斯基度量,

16.测地线方程2和 度规张量分量g的00分量.:
$$ 牛顿引力由两个方程组成:一个高速我们我们物质如何对引力做出反应,$$$$另一个告诉我们物质如何产生引力。 $$$$ 第一个方程是从牛顿第二定律中得到:$$$$ a = -\nabla\phi 表示加速度为a, \phi为力 (加速度为力的负梯度??) $$$$ 测地线方程描述的是仅受中立作用的粒子的世界线,因此我们的目标是证明,$$$$ 在牛顿极限的情况下,测地线方程可简化成第一个牛顿重力方程 $$$$ 测地线方程为:$$$$ 0 = \frac{d^2 x^\beta}{d\tau ^2 }+\Gamma_{\mu \nu}^\beta \frac{\partial x^\mu}{\partial \tau} \frac{\partial x^ \nu}{\partial \tau} $$$$ 因为粒子运动缓慢所以时间分量支配了其他分量, $$$$ 因此我们可以近似的得出: 由于: \frac{dx^i}{d\tau } \ll \frac{dt}{d\tau} $$$$ 0 = \frac{d^2 x^\beta}{d\tau ^2 }+\Gamma_{\mu \nu}^\beta \frac{\partial x^\mu}{\partial \tau} \frac{\partial x^ \nu}{\partial \tau} $$$$≈ \frac{d^2 x^\beta}{d\tau ^2 }+\Gamma_{00}^\beta (\frac{cdt}{d\tau} )^2 \frac{d^2 x^i}{d\tau ^2 }+\Gamma_{00}^i (\frac{cdt}{d\tau })^2= 0 公式1 $$$$ 前面提到Christoffel符号: \Gamma_{00}^i=\frac{1}{2} g^{ij} (g_{j0,0}+g_{j0,0}−g_{00,j} ) $$$$ 但是因为引力场很弱所以,所以时间导数g_{j0,0} 为0,$$$$ 因此,可以将christoffel 符号简化成 \Gamma_{00}^i=\frac{1}{2} g^{ij} g_{00,j} $$$$ 如果引力场足够弱,时空仅略微从狭义相对论的闵可夫斯基空间变形,$$$$ 我们可以考虑时空度量为一个小的扰动闵可夫斯基规度\eta_{\mu \nu} $$$$ 则g_{\mu \nu}=\eta_{\mu \nu}+h_{\mu \nu} , |{\mu \nu}|\ll 1 $$$$ g_{00,j}={(\eta_{00}+h_{00} )}_{,j} g_{00,j}= {\eta_{00}}_{,j} +h_{00,j}=0+h_{00,j} $$$$ 由于\eta_{00}=1 g_{00,j}=h_{00,j} $$$$ 在此步骤中,公式1变成: \frac{d^2 x^i}{d\tau ^2 }=− \Gamma_{00}^i \frac{cdt}{d\tau }^2 $$$$ \frac{d^2 x^i}{d\tau ^2 }= \frac{1}{2} g^{ij} h_{00,j} (\frac{cdt}{d\tau} )^2 $$$$ 如果我们定义 g^{ij}=\eta^{ij} −h^{ij}, 我们发现g^\mu\sigma g_{\sigma v}=\delta_ \nu^\mu, $$$$ 于是我们得到: $$$$ \frac{d^2 x^i}{d\tau ^2 }= \frac{1}{2} \eta^{ij} h_{00,j} (\frac{cdt}{d\tau} )^2 (\eta来度量g) $$$$ \eta^{ii}=−1, 其他值为0,所以: $$$$ \frac{d^2 x^i}{d\tau ^2 }= −\frac{1}{2} h_{00,i} (\frac{cdt}{d\tau} )^2 $$$$ 将左侧的导数从\tau 改成t,为此,首先将上式中的i替换成0: $$$$\frac{c^2 d^2 t}{d\tau ^2 }=−\frac{1}{2} h_{00},0 \frac{cdt}{d\tau}^2 $$$$ c^2 \frac{d^2 t}{d\tau ^2 }=0 (因为重力场是常数 h_{00},0=0) $$$$ \frac{d^2 t}{d\tau ^2 }=0, $$$$ 有了这个结果,我们仍然需要对\tau 使用偏导数 $$$$ \frac{d^2 x^i}{d\tau ^2 }=\frac{d}{d\tau} \frac{dx^i}{d\tau} =\frac{d}{d\tau} (\frac{dt}{d\tau} \frac{dx^i}{dt}) = $$$$ \frac{d}{d\tau} (\frac{d}{d\tau} \frac{dx^i}{d\tau} )+\frac{dx^i}{dt} (\frac{d}{d\tau} \frac{dx^i}{dt})=\frac{dt}{d\tau } (\frac{dt}{d\tau} \frac{d}{d\tau } \frac{dx^i}{d\tau})+\frac{dx^i}{dt} (\frac{d}{d\tau} \frac{dt}{d\tau} ) $$$$=(\frac{dt}{d\tau} )^2 (\frac{d^2 x^i}{dt^2} )+\frac{dx^i}{dt} (\frac{d^2 t}{d\tau ^2 }) $$$$ 所以 \frac{d^2 x^i}{d\tau ^2 }=(\frac{dt}{d\tau} )^2 (\frac{d^2 x^i}{dt^2} ) (制造出对t的偏导数) $$$$ 因为(\frac{d^2 t}{d\tau ^2} ) =0 $$$$ 那么 \frac{d^2 x^i}{d\tau ^2 }=(\frac{dt}{d\tau} )^2 (\frac{d^2 x^i}{dt^2} )=−\frac{1}{2} h_{00,i} (\frac{cdt}{d\tau} )^2 $$$$ \frac{d^2 x^i}{dt^2}=−\frac{c^2}{2} h(00,i) $$$$ 牛顿力学为\frac{d^2 x^i}{dt^2} =−\partial \frac{\phi}{\partial x^i} (\phi为牛顿引力势 ,可以把这个公式看成已知) $$$$ 最后,以向量形式表示: \frac{d^2 r}{dt^2} =−grad\phi 其中\phi=\frac{c^2 h_{00}}{2} $$$$ 备注: 将度规标准分量g_{00} 表示为: g_{00} =\eta_{00}+h_{00}=1+\frac{2\phi}{c^2} (就是将用\phi表示h_{00}) $$$$ 我们可以看到左侧的公制张量 与右侧的重力势之间存在直接联系 $$$$ 我们可计算地球上的h_{00} 可以得到其为10^(−9) 这意味着因重力场 $$$$而对于minkowski度量的偏差可以忽略不计。 $$

17.爱因斯坦的猜想与验证:
$$ 爱因斯坦张量微分形式比较,于是推测出 G_{\mu \nu}= \kappa T_{\mu \nu} $$$$ 爱因斯坦想要构造一个等式,左边是时空的弯曲情况,右边是时空中的能量。 $$$$ 可以看到已经有了T_{\mu \nu} 现在需要左边描述时空弯曲的程度, $$$$于是 G_{\mu \nu} 需要 满足 是一个二维张量就像T_{\mu \nu} 一样, $$$$ 应该描述使用曲率,并且相对黎曼张量是线性的,具有零散度,最后再牛顿极限下,$$$$应该减小到4\pi G\rho $$$$ 爱因斯坦的第一次尝试使用了Ricci张量作为解决方案: $$$$ 由 在牛顿极限下的测地线方程:\frac{d^2 r}{dt^2 }=−grad\phi 其中\phi=\frac{c^2 h_{00}}{2} $$$$ 可得到 将公制张量的分量 g_{00} 可以表示成 g_{00}= \eta_{00}+h_{00} =1+\frac{2\phi}{c^2} $$$$ 前面说到g_{\mu \nu} 非常重要就在于 它包含了所有关于时空和引力场的信息 , $$$$ 所以方程中应该也是类似g_{uv} 这种二阶导数的形式, $$$$ 爱因斯坦先考虑的是使用黎曼张量的收缩形式:Ricci张量: $$$$ 前面得到的黎曼张量的表达式为: $$$$ R_{abc}^d= \Gamma_{ac,b}^d −\Gamma_{ab,c}^d+\Gamma_{ac}^e \Gamma_{be}^d −\Gamma_{ab}^e \Gamma_{ce}^d $$$$ 在静态和弱引力场的情况下,只有 R_{00} 有贡献: $$$$ R_{00}=R_{00}a^\alpha =\Gamma_{0\alpha ,0}^\alpha −\Gamma_{00,a}^\alpha +O(h2 ) = −\Gamma_{00,i}^i $$$$ 前面提到牛顿极限下,$$$$ \Gamma_{00}^i=\frac{1}{2} g^{ij} (g_{j0,0}+g_{j0,0}−g_{00,j} ) (\eta^{ii}=−1 ? 其他值为0,所以:) $$$$ \Gamma_{00}^i=−\frac{1}{2} g^{ij} g_(00,j) , 因为g^{ij} 受\eta^{ij} 支配,并且 g_{00,j}=h_{00,j} $$$$ 所以\Gamma_{00}^i=−\frac{1}{2} \eta ^{ij} h_{00,j}=\frac{1}{2} \sigma _j^i h_{00,j} $$$$ \Gamma_{00,i}^i=\frac{1}{2} \sigma _j^i h_{00,ij} $$$$ R_{00}= −\Gamma_(00,i)^i =−\frac{1}{2} (\partial _1^2 h_{00}+\partial _2^2 h_{00}+\partial _3^2 h_{00} ) (00分量占主导) $$$$ =−\frac{1}{2} \nabla^2 h_{00}=−\frac{1}{c^2} \nabla^2 \phi $$$$ 爱因斯坦试图将R_{ab} 放在爱因斯坦方程的左侧,使他等于kT, $$$$ 他甚至用此解决了水星进动的问题,但是因为实际两边不等,所以最终爱因斯坦不得不放弃 $$$$ 爱因斯坦的第二次尝试: $$$$令等式左边为 G^{\mu \nu}=R^{\mu \nu} −\frac{1}{2} Rg^{\mu \nu} , $$$$其中 R 是ricci标量,这种形式的G_{ab} 是对称的,显然描述了时空曲率, $$$$因此只需证明总导数为0就像右侧的能动张量的导数为0 $$$$(表明能量守恒),为此,我们从bianchi \quad identity 开始: $$$$ \nabla_\sigma R_{\alpha \beta}{\mu \nu}+\nabla_ \nu R_{\alpha \beta \sigma \mu}+\nabla_\mu R_{\alpha \beta \nu\sigma} =0 $$$$ 每项都乘上 g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu} (因为 g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu} 的导数为0 ,所以可以把它们作为常数放到\nabla中) $$$$ \nabla_\sigma g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu} R_{\alpha \beta}{\mu \nu}+\nabla_ \nu g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu} R_{\alpha \beta \sigma \mu}+\nabla_\mu g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu} R_{\alpha \beta \nu\sigma} =0 $$$$ \nabla_\sigma g^{\gamma\sigma} R+\nabla_ \nu g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu} R_{\alpha \beta\sigma \mu}+\nabla_\mu g^{\gamma\sigma} g^{\alpha \mu } g^{\beta \nu} R_{\alpha \beta \nu\sigma} =0 $$$$ \nabla_\sigma g^{\gamma\sigma} R+\nabla_ \nu g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu }R_{\sigma \mu\alpha \beta}+\nabla_\mu g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu} R_ {\nu\sigma \alpha \beta}=0 $$$$ \nabla_\sigma g^{\gamma\sigma} R−\nabla_ \nu g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu} R_{\mu\sigma \alpha \beta}+\nabla_\mu g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu} R_ {\nu\sigma \alpha \beta}=0 $$$$ Ricci 张量可以表示成 R^{\mu \nu} =g^{\mu\beta} g^{v\sigma} r_{\beta\sigma } 上式改写为: $$$$ \nabla_\sigma g^{\gamma\sigma} R−\nabla_ \nu g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu } R_{\mu\sigma \alpha \beta}+\nabla_\mu g^{\gamma\sigma} g^{\alpha \mu} g^{\beta \nu} R_{\nu\sigma \alpha \beta}=0 $$$$ \nabla_\sigma g^{\gamma\sigma} R−\nabla_ \nu g^{\gamma\sigma} g^{\beta \nu} g^{\beta \nu} R_{\sigma \beta } +\nabla_\mu g^{\gamma\sigma} g^{\alpha \mu} R_{\sigma \alpha} =0 $$$$ \nabla_\sigma g^{\gamma\sigma} R −\nabla_ \nu R^{\gamma \nu}−\nabla_\mu R^{\gamma\mu}=0 $$$$ \nabla_\sigma g^{\gamma\sigma} R −\nabla_\sigma R^{\gamma\sigma} −\nabla_\mu R^{\gamma\sigma} =0 $$$$ \nabla_\sigma g^{\gamma\sigma} R −2\nabla_\sigma R^{\gamma\sigma} =0 $$$$ \nabla_\sigma (g^{\gamma\sigma} R −2R^{\gamma\sigma} )=0 $$$$ \nabla_\sigma (\frac{g^{\gamma\sigma} R}{2} −R^{\gamma\sigma} )=0 $$$$ 我们证明了爱因斯坦张量的散度为0 ,所以我们已经找到了爱因斯坦方程的左边部分 $$

18.常量K:
$$ 前面我们已经得到了爱因斯坦方程是G^{\mu \nu}=kT^{\mu \nu},需要确定常数k $$$$ 谓词需要证明对于静态和弱重力场下(牛顿极限)下,爱因斯坦方程可以简化成牛顿重力定律。 $$$$ 首先使用不同形式的爱因斯坦方程,在计算时能够更加容易一些。 $$$$ R^{\mu \nu}−\frac{1}{2} g^{\mu \nu} R=kT^{\mu \nu} $$$$ 两边同时乘g_{\mu \nu} 可以得到: $$$$ g_{\mu \nu} R^{\mu \nu} −\frac{1}{2} g_{\mu \nu} g^{\mu \nu} R=kg_{\mu \nu} T^{\mu \nu} $$$$ g_{\mu \nu} R^{\mu \nu}=R 并且 g_{\mu \nu} T^{\mu \nu}=T 所以: $$$$ R−\frac{1}{2} Rg_{\mu \nu} g^{\mu \nu}=kT $$$$ 因为g^{\mu \nu} 是g_{\mu \nu} 的逆 ,他们的乘积是I,因为使用contraction $$$$所以 g_{\mu \nu} g^{\mu \nu}=\delta_ \nu^ \nu =1+1+1+1=4 $$$$ 因此 R −\frac{1}{2} R× 4=kT $$$$ R = -kT , 将它代入到原式中 $$$$ R^{\mu \nu} −\frac{1}{2} g^{\mu \nu}× (−kT )= kT^{\mu \nu} $$$$ R^{\mu \nu}+\frac{1}{2} kg^{\mu \nu} T= kT^{\mu \nu} $$$$ R^{\mu \nu}=k(T^{\mu \nu} −\frac{1}{2} g^{\mu \nu} T) $$$$ 前面我们证明了分量R_{00}≈−\frac{1}{c^2} \nabla^2 \phi $$$$ 但是我们可以指出,当度量从固定时空减少到度量\eta时 ,我们可以通过Ricci张量的定义得到 $$$$ R^{00}=g^0\mu g^0 \nu R_{\mu \nu}≈\eta^0\mu \eta^0 \nu R_{\mu \nu} =(−1)(−1) R_{00} =R_{00} $$$$ R^{00}≈−\frac{1}{c^2} \nabla^2 \phi $$$$ 牛顿限制也意味着 T^{00}=\rho c^2 (因为T = \rho u^u u^ \nu 并且 u^i \ll u^0=c) $$$$ T = g_{\mu \nu} T^{\mu \nu}≈g_{00} T^{00}≈\eta_{00} T^{00}=T^{00} =\rho c^2 $$$$ K再代入R^{\mu \nu}=k(T^{\mu \nu} \frac{1}{2} g^{\mu \nu} T) $$$$ R^{00}=k(T^{00} −\frac{1}{2} \eta^{00} T) $$$$ −\frac{4\pi G\rho }{c^2} =K(\rho c^2 −\frac{1}{2}×1×\rho c^2 ) $$$$ −\frac{4\pi G\rho }{c^2} =\frac{1}{2} K\rho c^2 $$$$ K = -\frac{8\pi G}{c^4} $$$$ 终于我们得到了完整的爱因斯坦方程R_{\mu \nu} −\frac{1}{2} g_{\mu \nu} R=−8\pi GT_{\mu \nu} $$
当完全写出时,EFE(爱因斯坦场方程)由10个耦合的非线性二阶偏微分方程组成, 本来是16个,前面讲到对于对称的进行了合并,实际上解爱因斯坦方程就是在解度规张量g,所以相应的方程数为未知数的个数.文章末尾会有github上一个repo提供了对解的验证,对于正确的解会提供对应的方程中特殊部分的值如黎曼张量等
本文提及的场方程仅仅是最基础版本的,后来爱因斯坦又在方程中加入了一项宇宙常数,因为他认为宇宙是静态的,而原始方程解出来是确实膨胀的,所以加了一项常数抵消,但是哈勃证明了他的错误,但宇宙常数最后还是被留下来,用来表示宇宙中存在的暗物质和暗能量
参考文章
爱因斯坦场方程推导过程的逻辑梳理:
https://wenku.baidu.com/view/5c305d42ce84b9d528ea81c758f5f61fb7362863.html
本文主要来源,强推,有非常完整的描述:
Einsteinrelativelyeasy http://einsteinrelativelyeasy.com/index.php
另一些类似的网站:
还有对伽利略和麦克斯韦的成果介绍:
http://www.einstein-online.info/spotlights/gr.html
http://newt.phys.unsw.edu.au/einsteinlight/
对偶空间和对偶基的理解:
https://blog.csdn.net/sumx2015/article/details/78909635
维基百科
百度百科
参考视频:
场方程推导:
协变与逆变向量:
张量的基本运算(包括收缩):
代码:
spacetimeengine:
github上一个repo提供了对解的验证,对于正确的解会提供对应的方程中特殊部分的值如黎曼张量等 solution_array = [ metric, coordinate_set, index_config, cosmological_constant ] 仅需要输入解数组,其中包括了度规和,坐标表示,上下标配置,和宇宙常数即可进行验证
posted on 2019-11-09 22:32 CaptainHook 阅读(3209) 评论(0) 收藏 举报


 浙公网安备 33010602011771号
浙公网安备 33010602011771号