Splay基本操作
我们以一道题来引入吧!
题目说的很清楚,我们的数据结构要支持:插入x数,删除x数,查询数的排名和排名为x的数,求一个数前驱后继。
似乎用啥现有的数据结构都很难做到在O(nlogn)的复杂度中把这些问题全部解决……(别跟我说什么set,vector……)
所以我们来介绍一种新的数据结构——平衡树splay!
什么是平衡树呢?这是一种数据结构,满足以下性质:
1.它是一棵二叉树
2.对于任意一个节点,它的左子树中的任意一个节点的权值比他小,右子树中任意一个节点的权值比他大
3.一棵平衡树的任意一棵子树也是一个平衡树(其实第二条已经说明了这个事了)
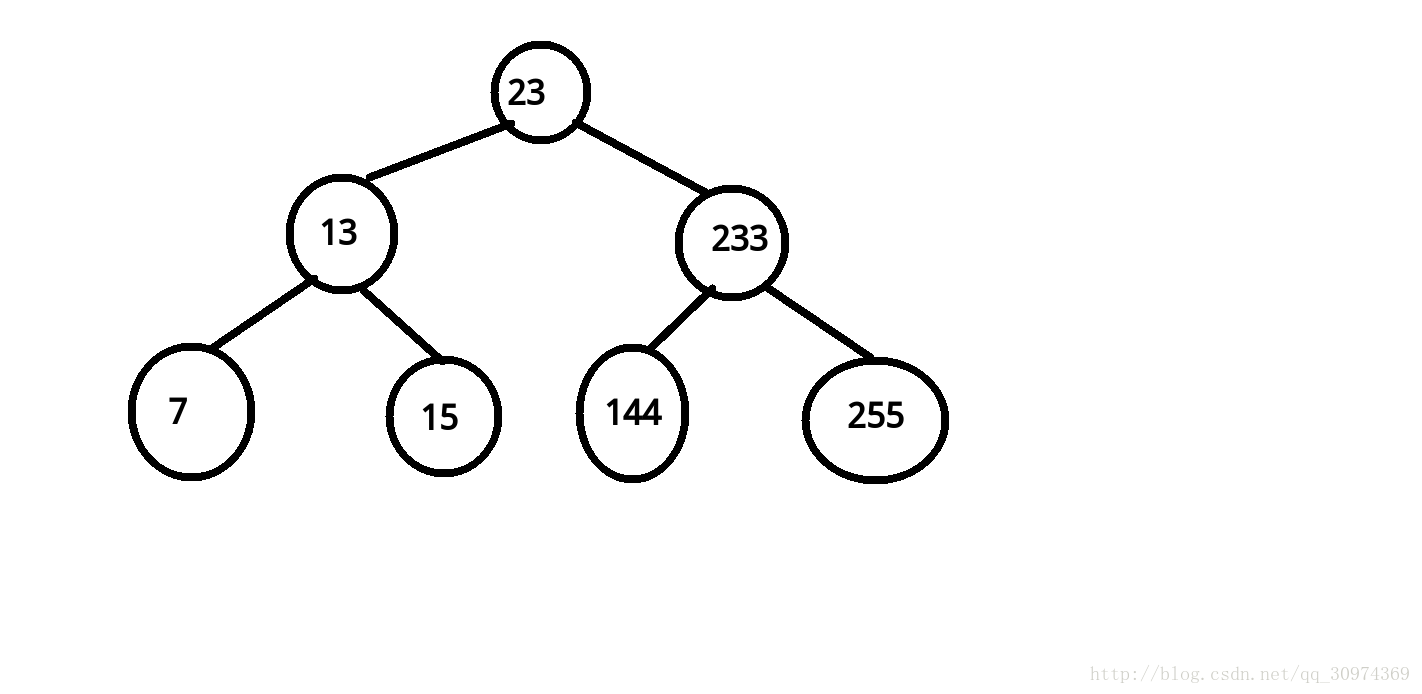
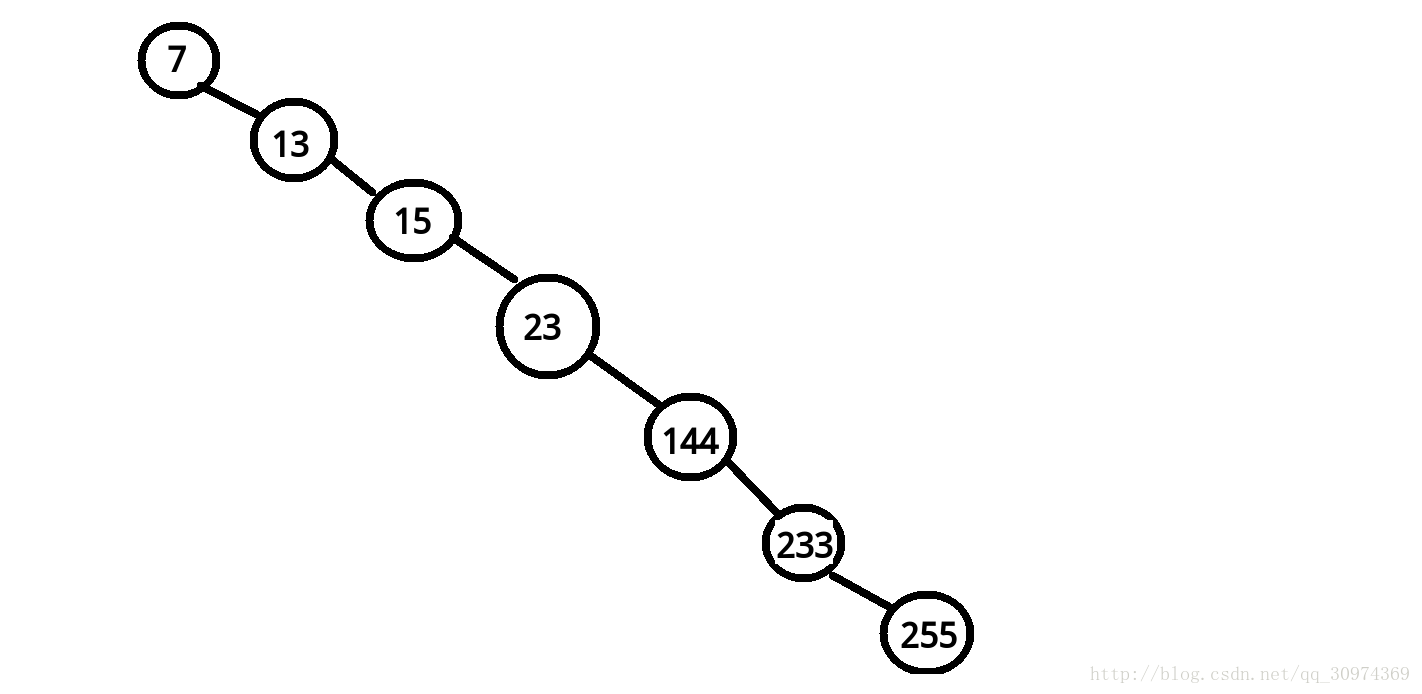
比如说这就是一棵平衡树(偷了yyb神犇的图),它现在非常优秀,深度是logn的。但是如果向一条链上插入多个数,或者出现什么奇怪的操作使平衡树退化为链,那么再进行查找等操作是很慢的,最坏甚至会到O(n)……比如下面这样(仍然偷了yyb神犇的图)
平衡树本身是可以支持上面所说的这些查询操作的(因为自身本身优秀的性质使得其可以进行二分),但是为了解决他有可能退化为链的这么个问题,神犇tarjan发明了一种新的数据结构——splay。
splay(伸展树),核心操作是rotate和splay(多个rotate),以使得对于每次操作之后树依然能保持一个良好的身材,使之不至于被退化为链,每次操作都能快速的在O(logn)中完成。这种操作使得每次改变之后这棵树仍然是一颗平衡树,但是节点的顺序发生了一些改变使得深度保持稳定。我们来看个图理解一下。
(以下图均偷自yyb神犇)
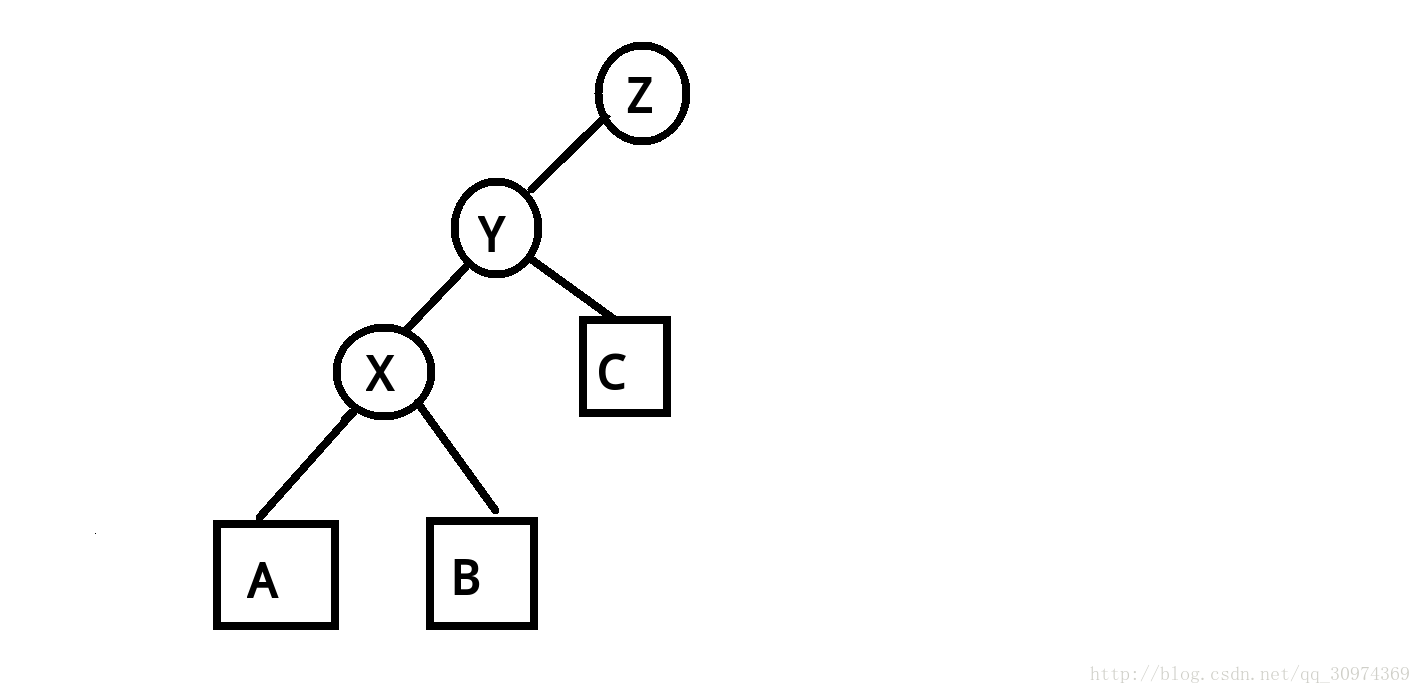
如图,x,y,z是三个节点,A,B,C是三棵子树。因为是一棵平衡树所以现在必然满足x<y<z.
现在我们看似乎x所在的那一侧有点长……所以我们不妨尝试把x旋转到y的位置,这样就能重构这棵树的结构,或许能使这棵树的深度变得更优。
首先我们肯定要保证新构成的树还是一棵平衡树,所以对于x,y,z三个节点,必然x,y还是在z的左子树中,既然把x移动到y的位置,那么x自然就成了z的左子树。不过平衡树还是一棵二叉树,那么y节点肯定不能呆在那了,它应该去哪呢?
我们思考一下,首先因为必须满足y>x,y<z,而x又是z的左儿子,所以y必然在x的左右子树中。而y还比x大,所以y自然应该在x的右子树中。那我们就直接把y变成x的右儿子就好啦!不过这样的话,x,y的子树又应该怎么办呢?x原来是y的左儿子,现在x成了y的父亲,那么y的左儿子那个位置肯定是空的,然后又因为x现在右儿子是y,它原来的右儿子多了出来(就是上面图的B)。B必然保证所有节点都<y,y现在还缺左儿子,所以直接把B变为y的左子树即可。
这样它就变成了这个样子,而且仍然是一棵平衡树。(上面已经说明过了,也可以自己看看验证一下)
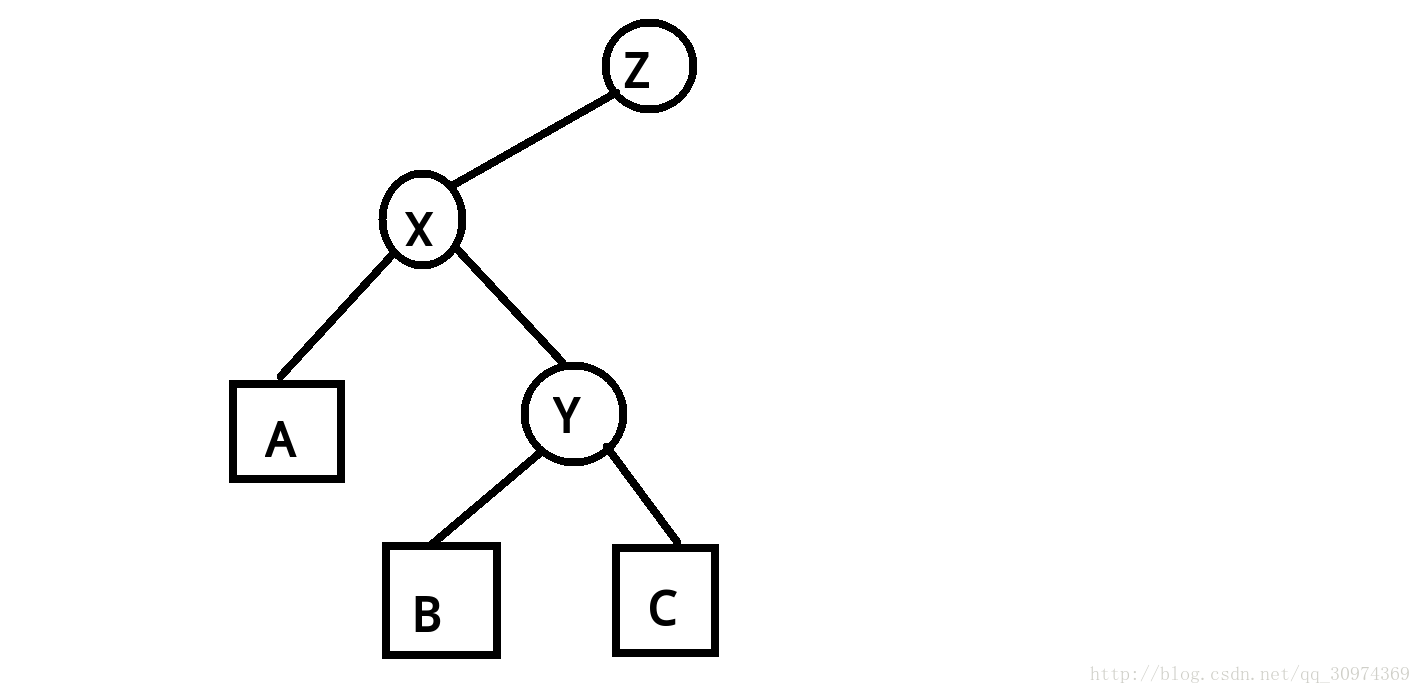
不过其实不只有这一种情况,x,y,z之间的关系一共有四种,随便推一推画一画就能看出来。
但是我们不可能写四个函数的对吧!所以我们要找出其中的普遍性规律,使得我们写一个函数就能解决问题。
首先因为肯定是用x去代替y,那么y是z的哪个儿子,转化之后x也必然是z的哪个儿子。
之后,我们又发现,一开始x是y的哪个儿子,那么在进行一次转变之后x的那个儿子就不会变化。为什么呢?假如说现在x是y的右儿子,那么必然满足x>y.而经过一次转变之后,x成为了z的一个儿子,那么y只能成为x的其中一个儿子(这个上文已经提到过了),那么现在y<x,y自然就成为了x的左儿子,相对应的x左儿子移动,右儿子并没有变化。反过来也是一个道理。
简单的来说就一句话:x是y的哪个儿子,那么相对应的x的那个儿子一定比其父亲(x)在权值方面(大/小)更优,所以y必然不会更新到它。
最后就很容易看出来了,x是y的哪个儿子,y就会成为x与之相对应的儿子(比如x是y的左儿子,y就会成为x的右儿子)
总结一下:(直接抄yyb神犇的话了,比较简洁)
所以总结一下:
1.X变到原来Y的位置
2.Y变成了 X原来在Y的 相对的那个儿子
3.Y的非X的儿子不变 X的 X原来在Y的 那个儿子不变
4.X的 X原来在Y的 相对的 那个儿子 变成了 Y原来是X的那个儿子
我们上一份代码来看一下吧!
bool get(int x)//get用于返回当前节点是自己父亲的哪个儿子 { return t[t[x].fa].ch[1] == x; } void pushup(int x) { t[x].son = t[t[x].ch[0]].son + t[t[x].ch[1]].son + t[x].cnt; }//更新自己为根的子树大小,其中cnt是这个数出现的次数 void rotate(int x)//旋转操作 { int y = t[x].fa,z = t[y].fa,k = get(x); t[z].ch[t[z].ch[1] == y] = x,t[x].fa = z;//更改z节点的儿子,x节点的父亲 t[y].ch[k] = t[x].ch[k^1],t[t[y].ch[k]].fa = y;//更改y节点的一个儿子和它的父亲 t[x].ch[k^1] = y,t[y].fa = x;//更改x节点的儿子和y节点的父亲 pushup(x),pushup(y);//更新状态 }
是不是炒鸡好理解呀QWQ
那么splay最核心的操作我们就说完了。下面我们再来说说splay操作!(要不这玩意为啥叫splay啊……)
其实splay操作就是rotate操作的叠加,本来rotate操作是很优秀的一种操作,不过实际上还会发生一些奇怪的事情,我们要考虑这样一些问题。
比如说我们看这样一棵平衡树。

好的,如果你直接两次右rotate把x旋到z的位置,那么你将得到这样一棵平衡树:
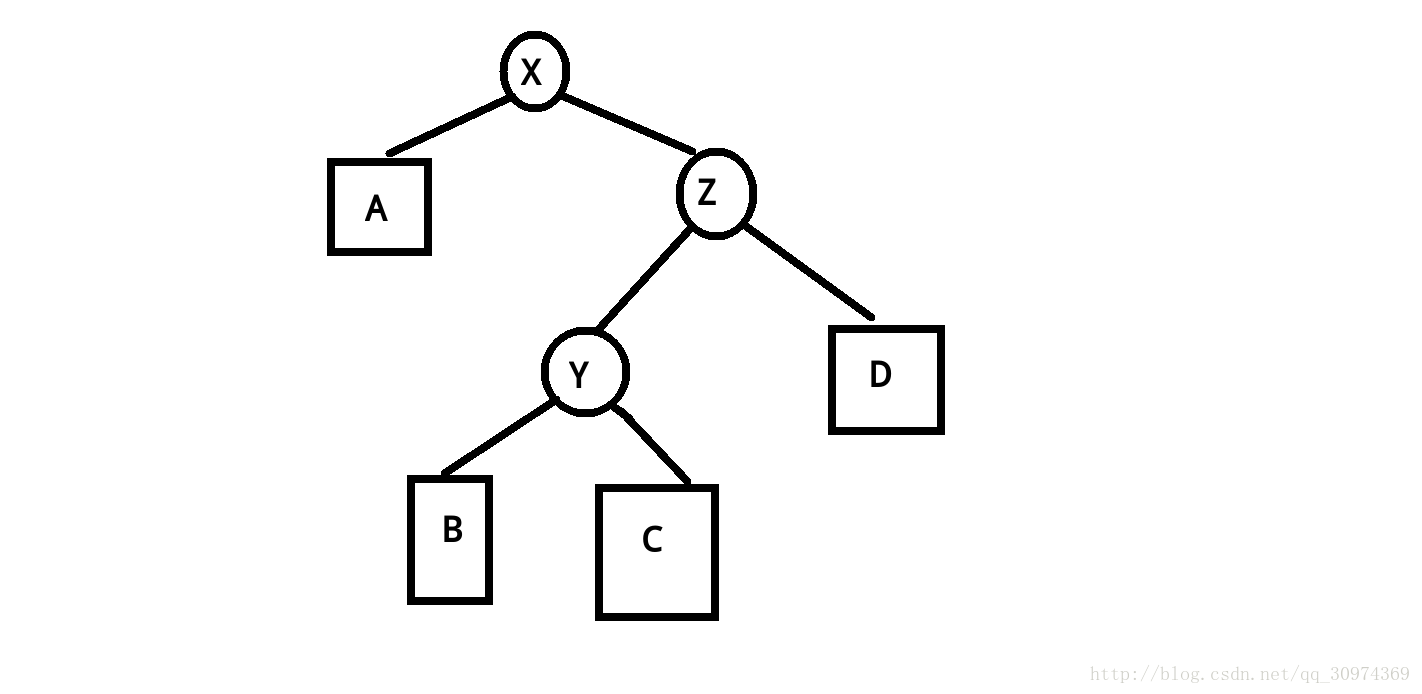
我们仔细观察之后发现一个神奇的问题,有一条链其实没有发生长度变化。就是z-y-x-b这条链,两次旋转之后变成了z-x-y-b,但是本身的长度是没有改变的。
这样splay就容易被卡,比如你一直往这条链里面插入元素,它可能就变得很长很长很长,你查询的速度又会很慢很慢很慢。
那咋办?难道伟大的splay就不能实现了嘛?当然不是,我们只要更改一下rotate的办法即可。对于上面这种状况,我们可以自己手画一下,如果先把y旋转到z的位置,再把x旋转到y的位置,这条链的长度就缩短了。
这个也是有普遍性结论的!我们发现如果x,y是y,z的同一个儿子,那么就先旋转y再旋转x,否则直接旋转两次x即可。(这段大家手画一下理解一下更好)
可能有人会提出这样的疑问,就是在更改了rotate顺序之后,当前这条链确实缩短了,但是相对的还有一(多)条链可能没有长度变化,这个不会被卡吗?
仔细想之后是不会的,因为我们每次splay操作是从当前被修改的节点开始的。所以只要保证当前所在链长度不会增大即OK。况且从长远来看,你构造出一个splay之后,它本身是会接近满二叉树的一种状态,你对其进行一次splay,它仍然是接近满二叉树的状态,故进过多次splay之后,这棵splay依然是接近满二叉树的良好身材。
我们来看一下splay操作的代码!
void splay(int x,int goal)//goal是要旋转到的目标节点 { while(t[x].fa != goal) { int y = t[x].fa,z = t[y].fa; if(z != goal) (t[y].ch[0] == x) ^ (t[z].ch[0] == y) ? rotate(x) : rotate(y);//对于左右儿子的讨论 rotate(x); } if(goal == 0) root = x;//更改根节点 }
ovo其实到这里splay最核心的俩操作已经结束了。那我们来继续说一说怎么支持上面的这些操作。
首先是查找find操作,查找一个数的位置。对于一个节点,左面全比他小,右面全比他大,那我们就可以直接愉快的二分,向左/右递归即可。然后我们把这个节点splay到根,方便接下来肆意(划死)操作。
我们直接看代码吧!
void find(int x) { int u = root; if(!u) return; while(t[u].ch[x > t[u].val] && x != t[u].val) u = t[u].ch[x > t[u].val];//通过x和当前节点值的大小比较来确定应该向哪里递归 splay(u,0); }
然后是insert操作,插入一个数。我们首先找到这个数在平衡树中哪个位置,如果这个节点已经存在的话,那我们把这个节点出现次数++,否则直接新建一个节点。
void insert(int x) { int u = root,f = 0; while(u && t[u].val != x) f = u,u = t[u].ch[x > t[u].val]; if(u) t[u].cnt++; else { u = ++idx; if(f) t[f].ch[x > t[f].val] = u; t[u].ch[0] = 0,t[u].ch[1] = 0; t[u].fa = f,t[u].val = x,t[u].cnt = 1,t[u].son = 1; } splay(u,0); }
在之后,前驱/后继操作(通过传0/1可以实现用一个函数同时找前驱/后继)。一个数的前驱就是其左子树中最靠右的节点,后继同理。
int next(int x,int f) { find(x); int u = root; if((t[u].val > x && f) || (t[u].val < x && !f)) return u;//如果当前节点权值大于x而且要找后继,或者当前节点权值小于x同时要找前驱 u = t[u].ch[f]; while(t[u].ch[f^1]) u = t[u].ch[f^1];//要往反方向跳 return u; }
当然我们可以选择分开写(这个是求根的前驱后继,实际使用的时候可以转化为先求一个点的编号再这样做)
int pre() { int u = t[root].ch[0]; while(t[u].ch[1]) u = t[u].ch[1]; return u; } int next { int u = t[root].ch[1]; while(t[u].ch[0]) u = t[u].ch[0]; return u; }
最后是删除del操作。这个还是稍微有点麻烦。我们首先找到x的前驱,把它旋转到根,再找到x的后继把它旋转到当前的根(x的前驱)的右子树,那么这个时候x的后继的左子树里面就只可能有x,把它删了。如果出现次数大于1就cnt--并且splay到根,否则直接删了完事。
void del(int x) { int la = next(x,0),ne = next(x,1); splay(la,0),splay(ne,la); int g = t[ne].ch[0]; if(t[g].cnt > 1) t[g].cnt--,splay(g,0); else t[ne].ch[0] = 0; }
哎不对,还有一个排名为x的数。这个也比较容易,我们还是用二分的思想即可。
int rk(int x) { int u = root; if(t[u].son < x) return 0; while(1) { int y = t[u].ch[0]; if(x > t[y].son + t[u].cnt) x -= (t[y].son + t[u].cnt),u = t[u].ch[1];//这时要向右子树找 else if(t[y].son >= x) u = y;向左子树找 else return t[u].val;//否则说明找到了,返回 } }
那我们就成功的用splay解决了这些问题!我们来看一下完整代码。
// luogu-judger-enable-o2 #include<cstdio> #include<algorithm> #include<cstring> #include<iostream> #include<cmath> #include<queue> #include<set> #define rep(i,a,n) for(int i = a;i <= n;i++) #define per(i,n,a) for(int i = n;i >= a;i--) #define enter putchar('\n') using namespace std; typedef long long ll; const int M = 100005; const int INF = 2147483647; int read() { int ans = 0,op = 1; char ch = getchar(); while(ch < '0' || ch > '9') { if(ch == '-') op = -1; ch = getchar(); } while(ch >= '0' && ch <= '9') { ans *= 10; ans += ch - '0'; ch = getchar(); } return ans * op; } struct node { int fa,son,ch[2],cnt,val; }t[M<<2]; int n,root = 0,idx,op,x; void pushup(int x) { t[x].son = t[t[x].ch[0]].son + t[t[x].ch[1]].son + t[x].cnt; } bool get(int x) { return t[t[x].fa].ch[1] == x; } void rotate(int x) { int y = t[x].fa,z = t[y].fa,k = get(x); t[z].ch[t[z].ch[1] == y] = x,t[x].fa = z; t[y].ch[k] = t[x].ch[k^1],t[t[y].ch[k]].fa = y; t[x].ch[k^1] = y,t[y].fa = x; pushup(x),pushup(y); } void splay(int x,int goal) { while(t[x].fa != goal) { int y = t[x].fa,z = t[y].fa; if(z != goal) (t[y].ch[0] == x) ^ (t[z].ch[0] == y) ? rotate(x) : rotate(y); rotate(x); } if(goal == 0) root = x; } void insert(int x) { int u = root,f = 0; while(u && t[u].val != x) f = u,u = t[u].ch[x > t[u].val]; if(u) t[u].cnt++; else { u = ++idx; if(f) t[f].ch[x > t[f].val] = u; t[u].ch[0] = 0,t[u].ch[1] = 0; t[u].fa = f,t[u].val = x,t[u].cnt = 1,t[u].son = 1; } splay(u,0); } void find(int x) { int u = root; if(!u) return; while(t[u].ch[x > t[u].val] && x != t[u].val) u = t[u].ch[x > t[u].val]; splay(u,0); } int next(int x,int f) { find(x); int u = root; if((t[u].val > x && f) || (t[u].val < x && !f)) return u; u = t[u].ch[f]; while(t[u].ch[f^1]) u = t[u].ch[f^1]; return u; } void del(int x) { int la = next(x,0),ne = next(x,1); splay(la,0),splay(ne,la); int g = t[ne].ch[0]; if(t[g].cnt > 1) t[g].cnt--,splay(g,0); else t[ne].ch[0] = 0; } int rk(int x) { int u = root; if(t[u].son < x) return 0; while(1) { int y = t[u].ch[0]; if(x > t[y].son + t[u].cnt) x -= (t[y].son + t[u].cnt),u = t[u].ch[1]; else if(t[y].son >= x) u = y; else return t[u].val; } } int main() { insert(INF),insert(-INF); n = read(); rep(i,1,n) { op = read(); if(op == 1) x = read(),insert(x); else if(op == 2) x = read(),del(x); else if(op == 3) x = read(),find(x),printf("%d\n",t[t[root].ch[0]].son); else if(op == 4) x = read(),printf("%d\n",rk(x+1)); else if(op == 5) x = read(),printf("%d\n",t[next(x,0)].val); else if(op == 6) x = read(),printf("%d\n",t[next(x,1)].val); } return 0; }
一开始插入INF和-INF的操作其实可以暂时忽略,那个是保证splay翻转区间时的正确性,还有好多其他实际题中的应用正确性的。(区间反转下次再说)
splay是不是很好理解呢?(不过代码讲真还是比较难记……)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号