可持久化数据结构入门

什么是可持久化数据结构呢？

简单一点来说，就是能支持访问以往某个版本的数据的数据结构，当然我的总结并没有那么贴切……

我们以这样一个事来引入吧！记得上学期的时候上数学课学统计，听辉哥在上面讲课，我在下面突然想到，能否写一种数据结构，能够快速访问每一个给定区间的中位数是多少？

考虑最暴力的做法就是每次sort取中间，但这样显然太慢了，然后如果在每个区间都建一棵权值线段树来维护，那空间又太大了。

所以我们引入一个新的强势数据结构——可持久化线段树（主席树）来解决这个问题！

为啥叫主席树呢？传说发明这种数据结构的神犇黄嘉泰，因为他在考试的时候不会写归并树就写了主席树这种东西替代归并树，并成功让广大OIer使用了这种数据结构，把归并树扔进了垃圾箱。因为他的名字缩写HJT也是当时chairman的名字缩写，故称为主席树。

言归正传。其实主席树相当于在每一个节点维护了一棵线段树（不是真的建了出来！）主席树节点中维护的值，是1-i之间这个区间内出现了数的次数。然后当我们查询的时候，就是利用到了前缀和的思想。

首先我们先偷大神的图来模拟一下建树的过程：感谢bestFY大神

7 1

1 5 2 6 3 7 4

2 5 3 

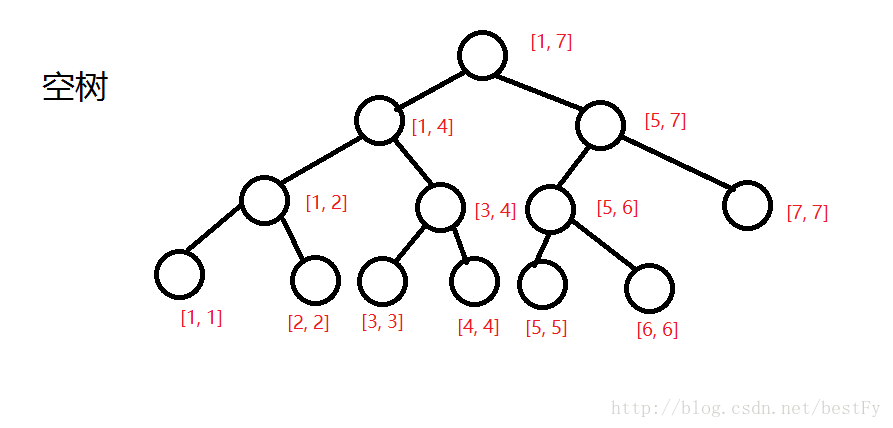
 然后开始插入，把经过的每一个节点的v++。

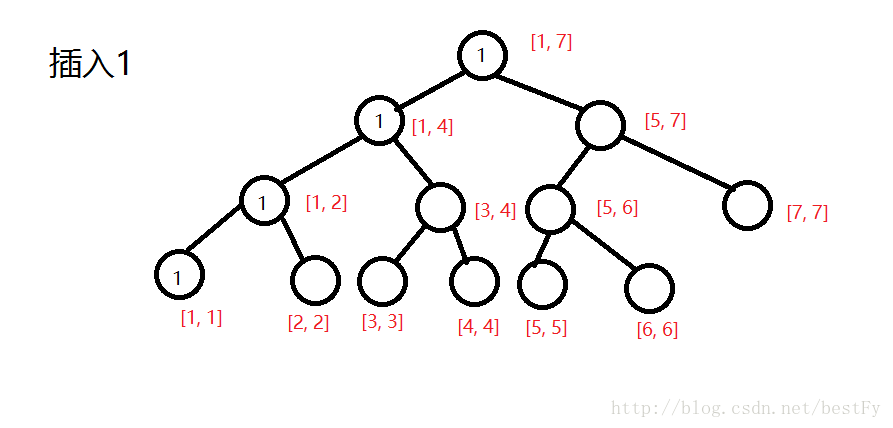
这样一直插入，直到最后把所有数插入完毕。

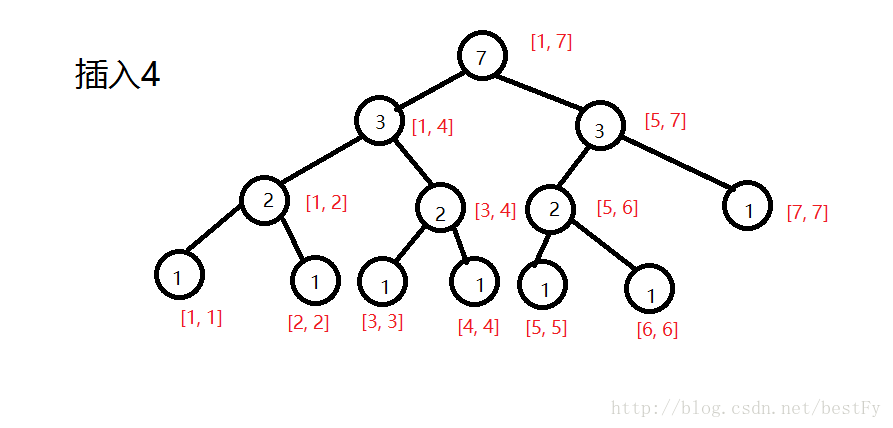
好的，那我们现在要查询。怎么查询呢？既然要查询[2,5]区间内第3大的数，那么就先把第一棵和第5棵线段树拿出来。

 

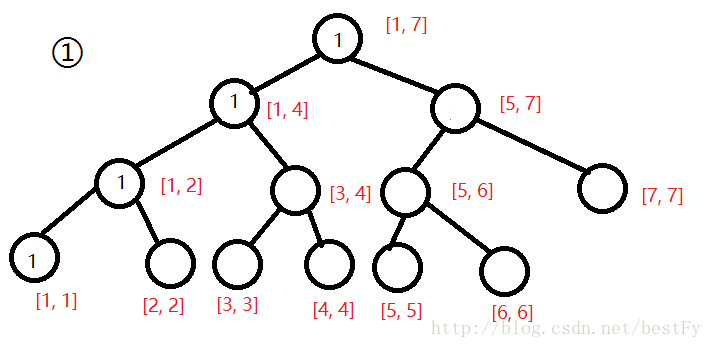
这时候我们惊奇的发现，对于每一个区间，我们用第5棵树中该区间的权值减去第一棵树中改区间的权值，发现delta就是在该范围的数在[2,5]中出现的次数！

这里其实是用到了前缀和的思想。仔细思考一下即可知。

这样的话我们就能在这棵delta树（这是沿用了兔哥的叫法）上进行k大值查询。只要像正常的权值线段树一样，如果当前数的排名大于左子树大小，就在右子树中找，否则在左子树中找就可以了。

不过实际上这棵树并不是这个样子的，上面的样子只是比较好理解，我们实际在操作的时候每修改一次就要新建一条链，不过我们只处理和本次修改操作有关的，无关的直接和原树共用即可。

然后我们就完成了。

传送门 看一下代码。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<queue>
#include<cstring>
#define rep(i,a,n) for(int i = a;i <= n;i++)
#define per(i,n,a) for(int i = n;i >= a;i--)
#define enter putchar('\n')
#define pr pair<int,int> 
#define mp make_pair
#define fi first
#define sc second
using namespace std;
typedef long long ll;
const int M = 200005;
const int N = 1000005;
 
int read()
{
    int ans = 0,op = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9')
    {
    if(ch == '-') op = -1;
    ch = getchar();
    }
    while(ch >='0' && ch <= '9')
    {
    ans *= 10;
    ans += ch - '0';
    ch = getchar();
    }
    return ans * op;
}

struct seg
{
    int lson,rson,v;
}t[N<<2];

int n,m,idx,a[M],h[M],tot,root[M],x,y,z;

void build(int &p,int l,int r)
{
    p = ++idx;
    if(l == r) return;
    int mid = (l+r) >> 1;
    build(t[p].lson,l,mid),build(t[p].rson,mid+1,r);
}

void modify(int old,int &p,int l,int r,int val)
{
    p = ++idx;
    t[p].lson = t[old].lson,t[p].rson = t[old].rson,t[p].v = t[old].v + 1;
    if(l == r) return;
    int mid = (l+r) >> 1;
    if(val <= mid) modify(t[p].lson,t[p].lson,l,mid,val);
    else modify(t[p].rson,t[p].rson,mid+1,r,val);
}

int query(int old,int now,int l,int r,int k)
{
    if(l == r) return l;
    int sum = t[t[now].lson].v - t[t[old].lson].v;
    int mid = (l+r) >> 1;
    if(k <= sum) return query(t[old].lson,t[now].lson,l,mid,k);
    else return query(t[old].rson,t[now].rson,mid+1,r,k-sum);
}

int main()
{
    n = read(),m = read();
    rep(i,1,n) a[i] = h[i] = read();
    sort(h+1,h+1+n);
    tot = unique(h+1,h+1+n) - h - 1;
    rep(i,1,n) a[i] = lower_bound(h+1,h+1+tot,a[i]) - h;
    build(root[0],1,tot);
    rep(i,1,n) modify(root[i-1],root[i],1,tot,a[i]);
    rep(i,1,m)
    {
    x = read(),y = read(),z = read();
    printf("%d\n",h[query(root[x-1],root[y],1,tot,z)]);
    }
    return 0;
}