AC自动机
AC自动机……(至于自动机是啥我也看不懂……请自行百度)
AC自动机简单来说可以被看成是trie树和KMP算法的结合体,它的用途主要是多模匹配,就是给你一个文本串和多个模式串,询问你诸如:有多少个模式串在文本串中出现过,或是什么模式串在文本串中出现了多少次之类的。
AC自动机的重点在于fail数组的构造。fail数组简单来说可以指当前字符串的一个后缀在这个trie树中所对应的最长的,且能与该后缀匹配的前缀的末尾位置。是不是很像KMP?我们说一下怎么构造fail数组。
首先按照构造trie树的方法构造一下模式串的trie树。这个应该不用说了……
构造fail数组的方法是bfs。首先,对于根结点上所连的点,把他们的fail全都设为root(就是0),并且把他们压入队列。之后每次取队列首元素,对于其子节点(v),首先跳转到当前节点的fail数组的位置(k),找这个节点(k)有没有与v相同的子节点(u),如果有,那么v的fail就是u,否则的话就再找k的fail,一直到找到或者回到root为止。
看样子写起来会很长……不过有这样一份代码。
void getfail() { rep(i,0,25) if(c[0][i]) fail[c[0][i]] = 0,q.push(c[0][i]); while(!q.empty()) { int k = q.front();q.pop(); rep(i,0,25) { if(c[k][i]) fail[c[k][i]] = c[fail[k]][i],q.push(c[k][i]); else c[k][i] = c[fail[k]][i]; } } }
这个是不是非常短呀?
重点在于这一句:c[k][i] = c[fail[k]][i];像是并查集一样,这样我们在求fail的时候只要访问一次fail就可以知道它的fail应该是什么了。
大家可能有疑问。正常求fail都是要一步步回推直到求出fail或者回到root,但是这种写法只有一次转移为什么是对的?画一个图看一下。
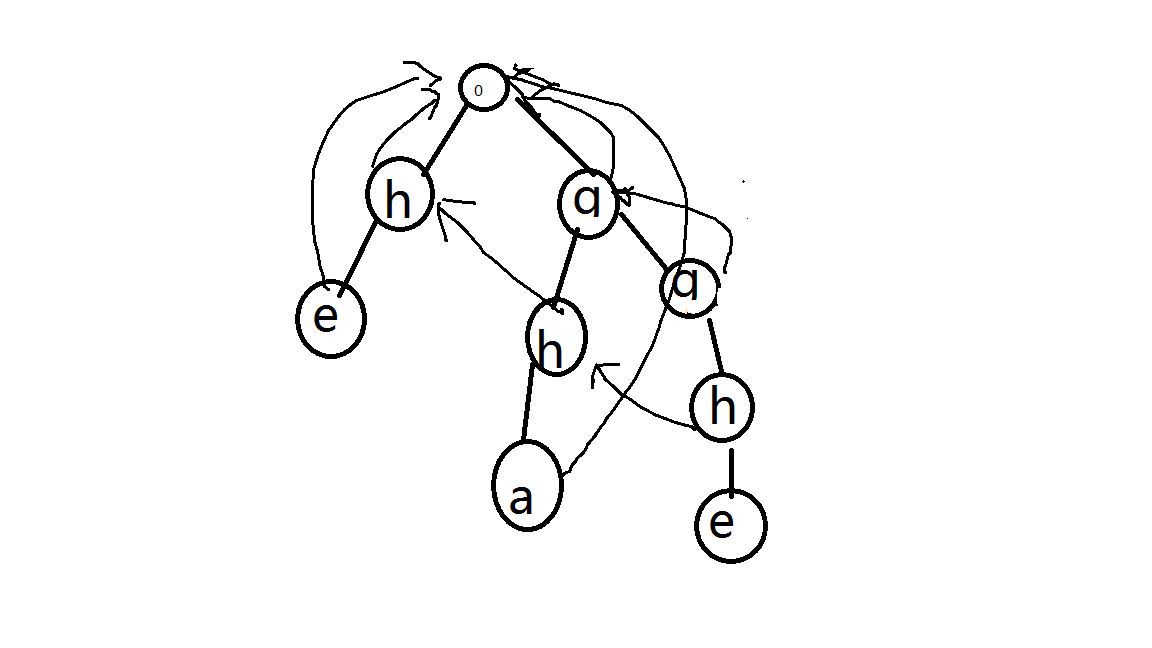
其中0是root节点。很显然,root的两个孩子的fail肯定是指向root的,之后我们看g下面的h,它的fail显然指向上一个h,就是s的儿子节点h。然后另一个g……下面的h的fail肯定也是指向上一个h 的。
之后问题来了,最后一个h下面的e,他的fail应该是第一个h下面的e,不过按照算法,因为第二个h的下面没有e,那么它的fail应该已经变为0,怎么能正确呢?
其实是因为在求第二个h的fail的时候,向下bfs的时候因为这个h为e的儿子是不存在的,所以他执行了上面那行代码描述的操作,也就是说它相当于在下面构造了一个虚拟的e(实际指向了第一个h下面的e),这样后面第三个h下面的e只需要跳一次fail,就能把自己的fail指针设为第一个h下面的e。
同样的,这个还有一个非常大的作用,在最后文本串匹配的时候每次匹配到末尾的时候是不需要自己手动返回root。因为对于一个叶子节点,它的fail肯定会往上面指,他会直接指到一个可继续匹配的地方。比如说刚才那个图,在匹配到第一个h下面的e的时候,它会自动跳回自己的fail指针的位置,也就是root继续去匹配。这个用fail指针的定义很好懂,因为你当前这段后缀是另一个字符串的前缀,从其fail的位置继续开始匹配更容易匹配到……一个会在文本串中出现的字符串。
这样就非常容易的把fail数组建好了。
之后就是匹配了。匹配其实很简单,只要在每次匹配的时候都向其fail跳一次看看能否匹配即可。注意要先符合条件。在每次匹配上的时候,我们把匹配数目++。(其他的基本上面都说好了……)
其中有一个优化,就是在匹配时fail回跳的过程中,如果一个节点并不是任意一个字符串的结尾,我们把他的权值设为-1(在每次回跳的时候遇到权值为-1的边就不会再走)
这个是因为题目的特殊性,我们只要求出来是否出现过即可。对于一个点,它在第一次跳跃的时候肯定会把其所能跳到的点上面的权值都加完,之后就不用再管了。
增强版其实也并不难。我们只要在每次匹配的时候把匹配次数++,并且记录是哪个字符串匹配了即可。注意这里不能像简单版一样把一个节点的权值赋成-1。(这个在luogu上卡掉了我第一个点……)
因为这个是要你求出出现了多少次。也就是说,对于一个点,它完全有可能被多次被跳到,如果把它设为-1会影响计算,似乎在字符串有重复的时候会出错。
看一下图。
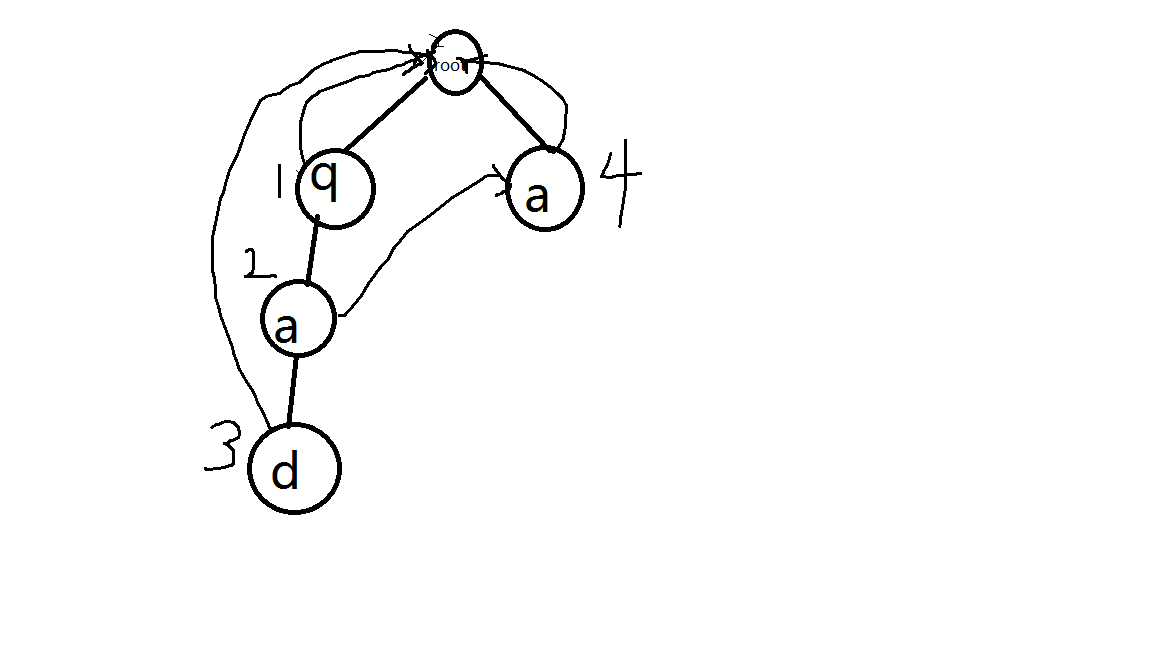
在匹配到第一个a的时候,由于这个a的权值是0,所以我们把它设成了-1,之后它跳到第二个a并且将a字符串的出现次数++.不过问题是如果文本串中还有一个“qad”,那就会导致在第二次访问的时候从第一个a的位置不会再转移到第二个a,也就会让字符串“a”少被算一次。所以就不要设为-1……好好匹配就行了。
这样就可以了,看一下代码。
简单版:
#include<cstdio> #include<algorithm> #include<cstring> #include<cmath> #include<queue> #define rep(i,a,n) for(int i = a;i <= n;i++) #define per(i,n,a) for(int i = n;i >= a;i--) #define enter putchar('\n') using namespace std; const int N = 500005; const int M = 1000005; typedef long long ll; int read() { int ans = 0,op = 1; char ch = getchar(); while(ch < '0' || ch > '9') { if(ch == '-') op = -1; ch = getchar(); } while(ch >= '0' && ch <= '9') { ans *= 10; ans += ch - '0'; ch = getchar(); } return ans * op; } queue<int> q; struct ACG { int c[N][26],val[N],fail[N],cnt; void ins(char *s) { int len = strlen(s); int now = 0; rep(i,0,len-1) { int v = s[i] - 'a'; if(!c[now][v]) c[now][v] = ++cnt; now = c[now][v]; } val[now]++; } void getfail() { rep(i,0,25) if(c[0][i]) fail[c[0][i]] = 0,q.push(c[0][i]);//对根的儿子求fail while(!q.empty())//bfs求fail { int k = q.front(); q.pop(); rep(i,0,25) { if(c[k][i]) fail[c[k][i]] = c[fail[k]][i],q.push(c[k][i]); else c[k][i] = c[fail[k]][i]; } } } int query(char *s) { int len = strlen(s); int now = 0,ans = 0; rep(i,0,len-1) { now = c[now][s[i]-'a']; for(int t = now; t && val[t] != -1; t = fail[t]) ans += val[t],val[t] = -1; } return ans; } }AC; int n; char p[M]; int main() { n = read(); rep(i,1,n) scanf("%s",p),AC.ins(p); AC.getfail(); scanf("%s",p); int ans = AC.query(p); printf("%d\n",ans); return 0; }
增强版:
#include<cstdio> #include<algorithm> #include<cstring> #include<cmath> #include<queue> #define rep(i,a,n) for(int i = a;i <= n;i++) #define per(i,n,a) for(int i = n;i >= a;i--) #define enter putchar('\n') using namespace std; const int N = 500005; const int M = 1000005; typedef long long ll; int read() { int ans = 0,op = 1; char ch = getchar(); while(ch < '0' || ch > '9') { if(ch == '-') op = -1; ch = getchar(); } while(ch >= '0' && ch <= '9') { ans *= 10; ans += ch - '0'; ch = getchar(); } return ans * op; } queue<int> q; int t,sum[200],maxn; char str[M],s[200][200]; struct ACG { int c[N][26],p[N],fail[N],cnt,d[N]; void clear() { memset(c,0,sizeof(c)); memset(fail,0,sizeof(fail)); memset(d,0,sizeof(d)); memset(p,0,sizeof(p)); cnt = 0; } void insert(char *s,int f) { int len = strlen(s),now = 0; rep(i,0,len-1) { int v = s[i] - 'a'; if(!c[now][v]) c[now][v] = ++cnt; now = c[now][v]; } p[now]++,d[now] = f; } void getfail() { rep(i,0,25) if(c[0][i]) fail[c[0][i]] = 0,q.push(c[0][i]); while(!q.empty()) { int k = q.front();q.pop(); rep(i,0,25) { if(c[k][i]) fail[c[k][i]] = c[fail[k]][i],q.push(c[k][i]); else c[k][i] = c[fail[k]][i]; } } } void match(char *s) { int len = strlen(s),now = 0; rep(i,0,len-1) { now = c[now][s[i] - 'a']; for(int g = now;g && p[g] != -1;g = fail[g]) { if(p[g]) sum[d[g]]++; //else p[g] = -1; } } } }AC; int main() { while(1) { t = read(); if(!t) break; AC.clear(),memset(sum,0,sizeof(sum)),maxn = 0; rep(i,1,t) scanf("%s",s[i]),AC.insert(s[i],i); AC.getfail(); scanf("%s",str),AC.match(str); rep(i,1,t) maxn = max(maxn,sum[i]); printf("%d\n",maxn); rep(i,1,t) if(sum[i] == maxn) printf("%s\n",s[i]); } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号